前言:
排序算法可以分为内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
常见的内部排序算法有十种:冒泡排序、选择排序、插入排序、希尔排序、堆排序、快速排序、归并排序、基数排序、计数排序、桶排序。
前面三种是简单排序,之后四种是在前面基础上进行优化,最后三种不是基于比较的排序,因此时间复杂度突破了nlogn的限制,但是算法本身对数据有一定的要求。本文主要基于C语言,依次介绍上述十大排序算法。
1 十大排序算法
1.1 冒泡排序
主要思想:依次对两个数比较大小,较大的数冒起来,较小的数压下来。
形象理解:一队新兵N个人整齐站成一列,教官想让他们按照身高排好队,看起来更协调,于是从前走到后走一趟,每次遇到相邻的两个人身高不协调时,就让两人互换位置。当走完一趟时,个子最高的人就被排到了最后。教官回到前排后发现队伍仍然不协调,于是又按照原样走了一趟。这样循环走了N-1趟之后,教官终于满意了。(注意:每次走一趟时,之前排到后面的高个子就不参与这次排序了;有时候可能还没走完N-1趟,教官就发现队伍已经协调了,于是排序结束。)
特点:简单易懂,排序稳定,但速度慢。
void Bubble_Sort(int A[], int N){ //冒泡排序
if(A==NULL || N<=1) return; //边界条件
int i, k, flag;
for(k=N-1; k>0; k--){ //跑N-1趟
flag = 0; //设置标记,如果发现某一趟没有交换数据,说明还未排序的序列已经有序了
for(i=0; i<k; i++){
if(A[i] > A[i+1]){
Swap_Two(&A[i], &A[i+1]);
flag = 1;
}
}
if(flag == 0) break;
}
return;
}
1.2 选择排序
主要思想:针对冒泡排序,有一个地方可以优化,即在跑一趟的过程中,没必要两两交换,可以先记下最小值,跑完一趟后直接将最小值换到前面。
特点:比冒泡更快一些,但代价是跳跃性交换,排序不稳定。
void Select_Sort(int A[], int N){ //选择排序
if(A==NULL || N<=1) return; //边界条件
int i, j, min_idx;
for(i=0; i<N-1; i++){
min_idx = i; //初始化最小值索引
for(j=i+1; j<N; j++){
if(A[j] < A[min_idx]) //若待排序列中有比当前最小值还小的,则更新最小值索引
min_idx = j;
}
if(min_idx != i) //若更新过最小值索引
Swap_Two(&A[i], &A[min_idx]);
}
return;
}
1.3 插入排序
主要思想:过程跟拿牌一样,依次拿N张牌,每次拿到到牌后,从后往前看,遇到合适位置就插进去。最终手上的牌从小到大。
特点:当数据规模较小或者数据基本有序时,效率较高。
void Insert_Sort(int A[], int N){ //直插排序
if(A==NULL || N<=1) return; //边界条件
int temp, i, k;
for(i=1; i<N; i++){
temp = A[i];
for(k=i-1; k>=0 && temp<A[k]; k--){
A[k+1] = A[k];
}
A[k+1] = temp;
}
return;
}
1.4 希尔排序
主要思想:设增量序列个数为k,则进行k轮排序。每一轮中,按照某个增量将数据分割成较小的若干组,每一组内部进行插入排序;各组排序完毕后,减小增量,进行下一轮的内部排序。
特点:针对插入排序的改进,当数据规模较大或无序时也比较高效。精妙之处在于,可以同时构造出两个特殊的有利条件(数据量小,基本有序),一个有利条件弱时,另外一个有利条件就强。(刚开始时虽然每组有序度低,但其数据量小;随着每轮的增量逐渐压缩,虽然各组数据量逐渐变大,但其有序度逐渐增加。)
void Shell_Sort(int A[], int N){ //希尔排序
if(A==NULL || N<=1) return; //边界条件
int k, i, j, p, temp;
int t = 0;
int D[33]; //假定增量序列不超过2^32
//定义Hibbard增量序列
for(k=1; k<33; k++){
t = 2 * t + 1; //增量序列项
if(t < N){
D[k] = t;
}else{
break;
}
}
//进行k-1(增量序列的个数)趟插排
for(p=k-1; p>=1; p--){
for(i=D[p]; i<N; i++){
temp = A[i];
for(j=i-D[p]; j>=0 && temp<A[j]; j-=D[p]){
A[j+D[p]] = A[j];
}
A[j+D[p]] = temp;
}
}
return;
}
1.5 堆排序
主要思想:将待排数组构建成一个最大堆,将堆顶最大元素换到后面,然后堆容量减1;类似进行N-1次操作即可。
void Perc_Down(int A[], int N, int i){ //在由N个结点组成的完全二叉树中,下滤第i个结点(从第0个结点算起),暂不做有效性检查
int parent, child, temp;
temp = A[i];
for(parent=i, child=2*parent+1; child<N; parent=child, child=2*parent+1){
if(child+1 < N && A[child+1] > A[child]) child++; //若右儿子存在,且数值更大,则child为右儿子
if(temp < A[child])
A[parent] = A[child];
else
break;
}
A[parent] = temp;
return;
}
void Heap_Sort(int A[], int N){ //堆排序
if(A==NULL || N<=1) return; //边界条件
int i;
//调整成最大堆
for(i=(N-2)/2; i>=0; i--){
Perc_Down(A, N, i); //在由N个结点组成的完全二叉树中,下滤结点i
}
//开始从后向前进行排序,注意每次交换后下滤时排除掉刚交换的最后一个
for(i=N-1; i>0; i--){
if(A[0] > A[i]){
Swap_Two(&A[0], &A[i]);
Perc_Down(A, i, 0);
}
}
return;
}
1.6 快速排序
主要思想:分治思想。选一基准元素,依次将剩余元素中小于该基准元素的值放置其左侧,大于等于该基准元素的值放置其右侧;然后,取基准元素的前半部分和后半部分分别进行同样的处理;以此类推,直至各子序列剩余一个元素时,即排序完成。
注意:对于小规模数据(n<100),快排由于用了递归,其效率可能还不如插排。因此通常可以定义一个阈值,当递归的数据量很小时停止递归,直接调用插排。
void Quick_Sort(int A[], int N){ //快速排序接口
if(A==NULL || N<=1) return; //边界条件
Quick_Sort_Core(A, 0, N-1);
return;
}
void Quick_Sort_Core(int A[], int left, int right){ //快排递归程序
if(left >= right) return; //若待排序列不到2个元素,则直接返回
int low, high, mid, temp;
//在三个点(端点和终点)中找出中间值,作为划分点。(也可以直接将left作为划分点,但若待排序列基本有序时就容易退化成冒泡)
mid = (left + right) / 2;
if(A[left] > A[mid]) Swap_Two(&A[left], &A[mid]);
if(A[left] > A[right]) Swap_Two(&A[left], &A[right]);
if(A[mid] > A[right]) Swap_Two(&A[mid], &A[right]);
if(right-left+1 <= 3) return; //若待排序列只有两个或三个元素,此时已排好序,直接返回
temp = A[mid]; //保存划分点
//至此三个点已有序
//用选择的点来切分给定数组
A[mid] = A[left+1]; //将空格移至left右侧,
low = left + 1;
high = right - 1;
while(low < high){ //跳出大循环时肯定有low==high
while(low < high && A[high] >= temp)
high--;
A[low] = A[high];
while(low < high && A[low] <= temp)
low++;
A[high] = A[low];
}
A[low] = temp;
//递归地排序左右子数组
Quick_Sort_Core(A, left, low-1);
Quick_Sort_Core(A, low+1, right);
return;
}
1.7 归并排序
归并排序,顾名思义就是合并两个有序数组。常见的归并排序有两种,递归法(自上而下的合并)和非递归法(自底向上的合并),都需要新开一个大小为n的数组来中转。递归法比较简单,就是中间切一刀,左右分别递归排序,最后合并两个有序数组。非递归法就是先分别对相邻的两个元素合并排序,第二趟时候分别对相邻的四个元素合并排序(此时前两个元素和后两个元素已有序),第三趟时候对相邻的八个元素合并排序,依次类推直至有序数组长度超过数组总长度。两者相较,递归的归并排序代码更简洁,代价是时间和空间复杂度上都会更大(因为有递归的logn)。下面的代码是非递归方法,后续对比也按照这个版本。
主要思想:类似两个有序链表的合并,每次两两合并相邻的两个有序序列,直至整个序列有序。
void Merge_Sort(int A[], int N){ //非递归的归并排序
if(A==NULL || N<=1) return; //边界条件
int len = 1; //有序序列的长度
int i, start, count = 0;
int *temp, *A1, *A2;
temp = malloc(N * sizeof(int)); //定义一个数组,作为A的副本,用于相互倒腾
while(len < N){ //若有序序列长度小于总长度
start = 0; //初始化起始位置
//先确定A1和A2
if(count % 2 == 0){
A1 = A;
A2 = temp;
}else{
A1 = temp;
A2 = A;
}
//根据有序序列长度,分别将A1中元素按成对列的方式合并至A2中
while(start + 2 * len <= N){ //注意start + 2 * len的实际含义是下标位置,可理解等号的原因
Merge_Sequence(A1, A2, start, start+len, start+2*len-1);
start += 2 * len;
}
//处理A1中剩下的尾巴
if(start + len < N) //若还有两个序列
Merge_Sequence(A1, A2, start, start+len, N-1);
else //若只剩一个序列。注意大bug:刚开始忘了这种情况
while(start < N){
A2[start] = A1[start];
start++;
}
//更新参数
len = 2 * len;
count++;
}
//如果最后数据存储在temp中,则需要将数据复制到A中
if(count % 2 == 1){
for(i=0; i<N; i++)
A[i] = temp[i];
}
free(temp);
return;
}
void Merge_Sequence(int A1[], int A2[], int start1, int start2, int end){ //合并A1中两个相邻有序序列,并将结果保存至A2中
//保证start2>start1 && end>=start2
int end1, end2, p;
end1 = start2 - 1;
end2 = end;
p = start1; //p指向A2中起始位置
//开始合并
while((start1 <= end1) && (start2 <= end2)){
if(A1[start1] <= A1[start2]) //注意带等号保证稳定性
A2[p++] = A1[start1++];
else
A2[p++] = A1[start2++];
}
//处理尾巴
while(start1 <= end1)
A2[p++] = A1[start1++];
while(start2 <= end2)
A2[p++] = A1[start2++];
return;
}
作为对比,也附上递归式的归并排序。
void MergeSort(int A[], int N) {
if (A == nullptr || N <= 1) return;
int *temp = new int(N);
MergeSort_Recursive(A, temp, 0, N - 1);
delete []temp;
}
void MergeSort_Recursive(int A[], int temp[], int left, int right) {
if (left >= right) return;
int mid = left + (right - left) / 2;
MergeSort_Recursive(A, temp, left, mid);
MergeSort_Recursive(A, temp, mid+1, right);
int p1 = left, p2 = mid + 1, p=left;
while (p1 <= mid && p2 <= right)
temp[p++] = (A[p1] <= A[p2]) ? A[p1++] : A[p2++];
while (p1 <= mid)
temp[p++] = A[p1++];
while (p2 <= right)
temp[p++] = A[p2++];
for (int i = left; i <= right; i++)
A[i] = temp[i];
}
1.8 基排序
主要思想:基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。
基排序的主要适用场景是待排元素是非负整数,且位数相差不大。此外,整数也可以用字符串等表达,所以也可以用于字符串的排序。
#define Radix 10
#define MaxDigit 4
typedef struct ENode{ //定义元素结点
int data;
struct ENode *next;
}*PtrToNode;
typedef struct BucketNode{ //定义桶结点结构
PtrToNode head;
PtrToNode tail;
}*Bucket;
void LSDRadix_Sort(int A[], int N){ //基排序
int i, D; //D为位, d为第D位上的数字(范围为0到9)
//定义两个大小为Radix的桶,并初始化
Bucket B1 = malloc(Radix * sizeof(struct BucketNode));
Bucket B2 = malloc(Radix * sizeof(struct BucketNode));
for(i=0; i<Radix; i++){
B1[i].head = B1[i].tail = B2[i].head = B2[i].tail = NULL; //注意大bug:B1为桶指针,但是B1[i]为结构体
}
//将数组中元素按照倒数第D位数字分别挂到桶B1上
D = 1;
Transfer_Array_To_Bucket(A, B1, N, D);
D++;
//开始相互倒腾,每倒腾一趟就往前看一位
while(D <= MaxDigit){
if(D % 2 == 0)
Transfer_Bucket_To_Bucket(B1, B2, D);
else
Transfer_Bucket_To_Bucket(B2, B1, D);
D++;
}
//倒腾结束后将桶中的元素依次倒入数组A中
if(D % 2 == 0)
Transfer_Bucket_To_Array(B1, A, N);
else
Transfer_Bucket_To_Array(B2, A, N);
//释放两个桶及其元素
Free_Bucket(B1);
Free_Bucket(B2);
return;
}
void Transfer_Array_To_Bucket(int A[], Bucket B, int N, int D){ //将数组A中元素按照第D位挂到桶B中
int i, d;
PtrToNode temp;
for(i=0; i<N; i++){
d = Get_Digit(A[i], D); //获取A[i]倒数第D位数字
temp = malloc(sizeof(struct ENode)); //创建一个新结点并初始化
temp->data = A[i];
temp->next = NULL;
if(B[d].tail == NULL){ //若桶的d位置上为空
B[d].head = B[d].tail = temp;
}else{
B[d].tail->next = temp;
B[d].tail = temp;
}
}
return;
}
void Transfer_Bucket_To_Array(Bucket B, int A[], int N){ //将桶B1中元素依次倒入数组A中,最多不超过N
int k, i = 0;
PtrToNode p;
for(k=0; k<Radix; k++){
p = B[k].head;
while(p != NULL){
if(i < N){
A[i++] = p->data;
p = p->next;
}else{
return;
}
}
}
return;
}
void Transfer_Bucket_To_Bucket(Bucket B1, Bucket B2, int D){ //依次将桶B1中元素按照第D位挂到B2中,
int k, d;
PtrToNode p, temp;
//依次从B1中取下元素结点,根据D位数字挂到B2上
for(k=0; k<Radix; k++){
p = B1[k].head;
while(p != NULL){
//从B1中取该元素,并获取第D位数字
temp = p;
p = p->next;
d = Get_Digit(temp->data, D); //获取该结点第D位数字
//将该元素挂到B2上
temp->next = NULL; //肯定作为本次转移的尾结点
if(B2[d].head == NULL){ //若B2[d]为空位置
B2[d].head = B2[d].tail = temp;
}else{ //若B2[d]不为空位置,则将temp结点接到尾结点上
B2[d].tail->next = temp;
B2[d].tail = temp;
}
}
//取完B1[k]上的所有结点后,设置其首尾结点指针为空
B1[k].head = B1[k].tail = NULL;
}
return;
}
int Get_Digit(int X, int D){ //获取X倒数第D位数字
int k, i;
for(i=0; i<D-1; i++)
X = X / Radix;
k = X % Radix;
return k;
}
1.9 计数排序
针对剑指offer中P81提到的场景,假如需要对公司内部几万个员工的年龄进行排序,要求时间复杂度为O(n),空间复杂度为O(1)。
主要思想:计数排序和前面的基排序类似,都是基于分桶思想。由于这里要求时间复杂度为O(n),低于基于比较的时间复杂度O(nlogn),所以前面7中排序算法均失效。又因为该场景中年龄属于一个比较小的范围,有大量的重复值,故可以考虑计数排序。实际做法是,新开一个长度为100的数组(假设年龄为0~99),数组下标表示年龄,数组存储该下标对应的年龄出现的个数,最后再根据数组的计数来排序。
计数排序主要适用场景是元素值比较集中,特别是集中在一个小区间里面。
//计数排序。应用场景:对公司几万个员工的年龄进行排序
void count_sort(int a[], int N){
if(a==NULL || N<=1) return;
const int largest = 99; //假设数值范围是0~99
int bucket[largest+1]; //申请100个桶,并清零。桶用来存储各个数值出现次数
for(int i=0; i<=largest; i++) //注意这里是 <= ,容易出错
bucket[i] = 0;
//遍历数组,桶记录各值出现次数
for(int i=0; i<N; i++){
if(a[i]<0 || a[i]>largest){
printf("Value is out of range!");
exit(-1);
}
bucket[a[i]] += 1;
}
//遍历各个桶,根据桶的记录值,对原数组进行排序
int index = 0; //原数组的下标
for(int k=0; k<=largest; k++){ //k为桶的下标
int num = bucket[k]; //数值为k的个数
for(int i=0; i<num; i++){
a[index] = k;
index++;
}
}
return;
}
1.10 桶排序
桶排序两大步骤:第一步是将值域划分成几个区间,然后将待排数组中各元素映射到这几个区间上(从区间这个大视角来看,这几个区间是有序的);第二步是针对各个区间内部元素,选择一个喜欢的算法进行排序。经过两步之后,整个数组就有序了。
桶排序是对计数排序的改进,计数排序申请的额外空间跨度从最小元素值到最大元素值,若待排序集合中元素不是依次递增的,则必然有空间浪费情况。桶排序则是弱化了这种浪费情况,将最小值到最大值之间的每一个位置申请空间,更新为最小值到最大值之间每一个固定区域申请空间,尽量减少了元素值大小不连续情况下的空间浪费情况。另外,从分桶的思想来看,快排也是一种分桶方法,即用一个pivot将值域切割成两个桶,左右分别递归。只不过快排是用一个pivot来切割值域,而桶排序则是直接将值域划分成几个区间。
桶排序的主要适用场景是,各元素值分布比较均匀,这样分桶时候就可以比较均匀,尽量避免把大部分元素都分到少数几个桶中。
2 十大排序算法比较
复杂度与稳定性的比较(来自维基百科)

以下是基于浙大数据结构课练习题测试(09-排序1 排序 (25 分)),由于后3种算法这里不适用,故只对比了前7种算法。
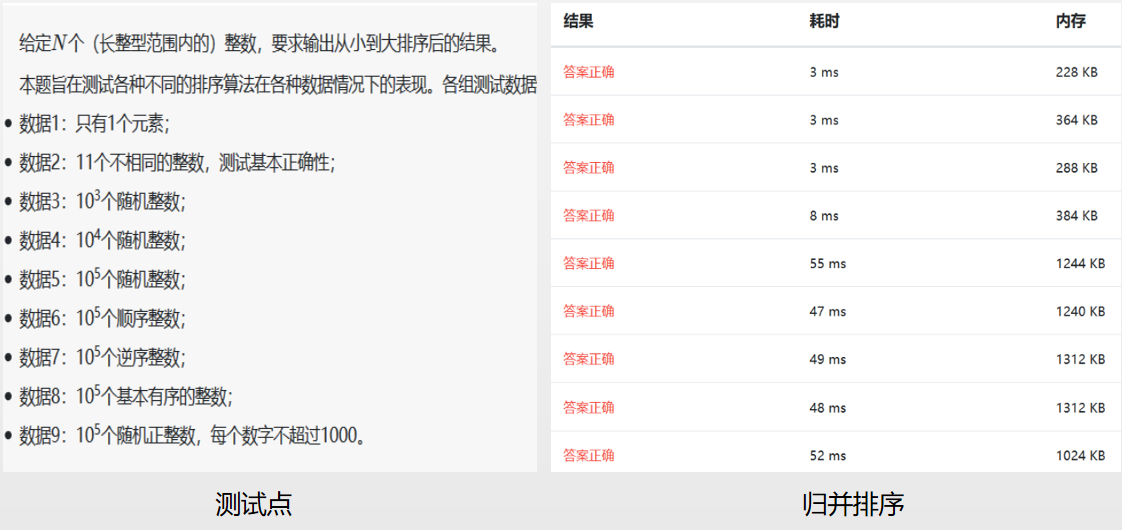
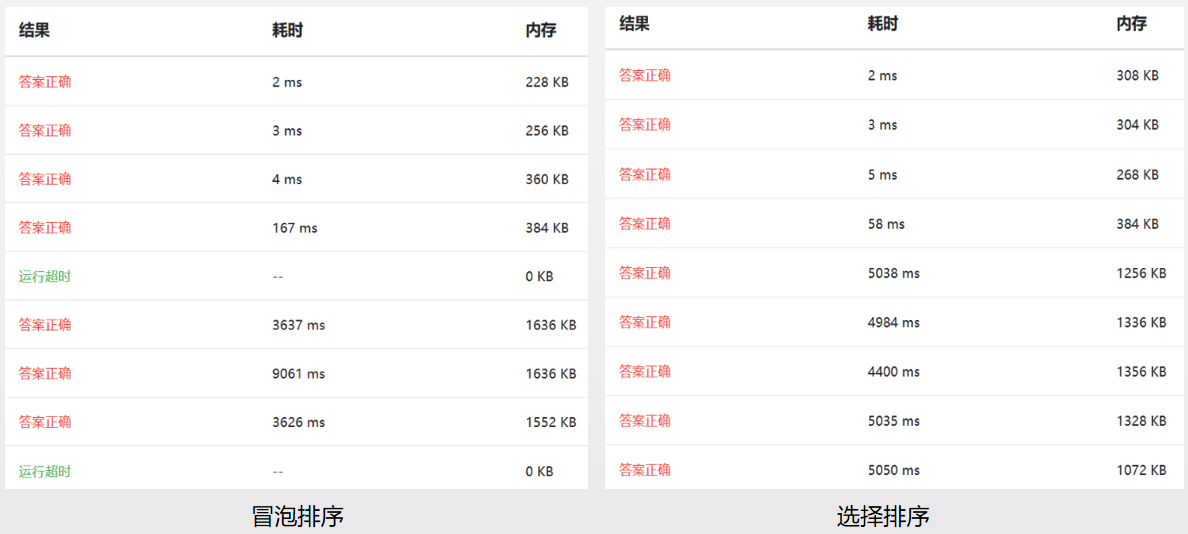
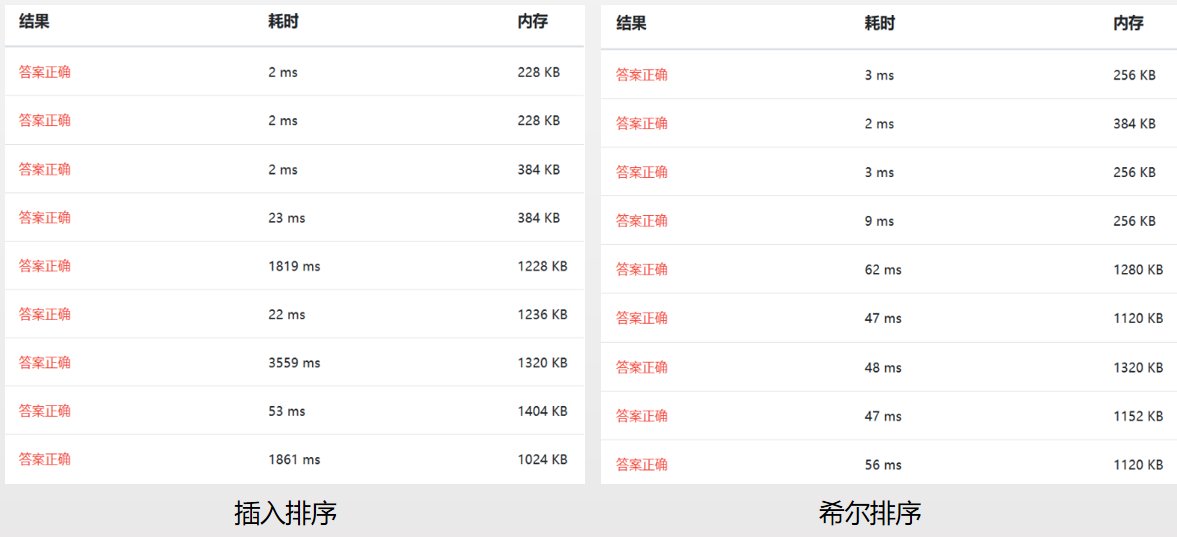
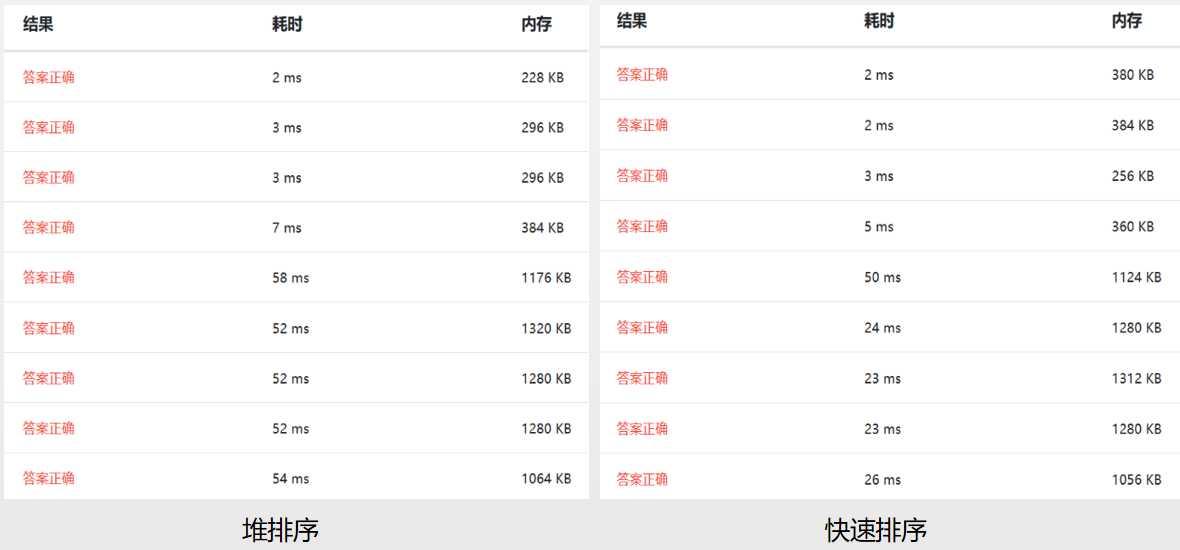
参考:
https://blog.csdn.net/qq_39207948/article/details/80006224
https://blog.csdn.net/qq_43152052/article/details/100078825
https://www.cnblogs.com/onepixel/articles/7674659.html
https://www.runoob.com/w3cnote/sort-algorithm-summary.html
https://github.com/francistao/LearningNotes/blob/master/Part3/Algorithm/Sort/面试中的 10 大排序算法总结.md