这是一篇学习笔记,原视频传送门。此人讲解十分清楚,唯一缺点是印度英语口音不好辨识。
学习B树和B+树,需要从以下几方面来理解,直接上来整定义,很难懂。
知识点如下:
1. 磁盘结构
2. 数据如何在磁盘中存储
3. 什么是索引
4. 什么是多级索引
5. m-way搜索树(二叉搜索树BST的推广)
6. B树
7. B树的插入和删除
8. B+树

一、磁盘结构
磁盘(硬盘)中存储介质是圆形的,类似光盘。数据记录在这些圆盘上(别问怎么存的,问就是不懂).那么怎么在圆盘上进行定位呢?
类似于平面直角坐标系, 我们用x轴和y轴, 任何一个点只要知道(x,y)坐标即可定位.
磁盘上,我们用磁道(track)和扇区(sector)来定位. 磁道就是一圈一圈的同心圆,扇区就是把大圆切成的几个大扇形.
所以用(trackno, sectorno)这个坐标就可以定位到一个块(block), 数据就存在这个block里, 块是存储的最小单元, 通常大小为512字节.
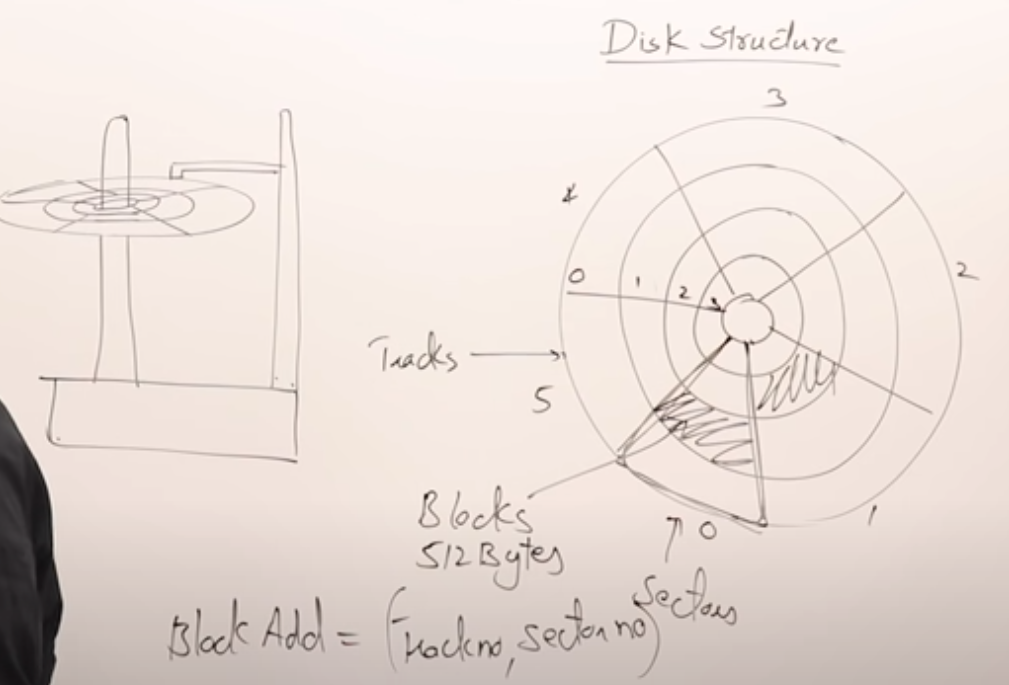
能够定位到一个块了, 但这个块有512个字节, 所以还得一个offset偏移量, 来准确把数据定位到究竟是哪一个字节.
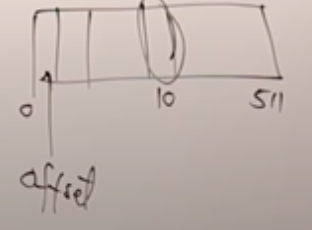
程序从硬盘里读取数据到内存,计算机学科中的研究领域也在此分为两部分,研究(内存中的)数据及其关系就是数据结构, 研究数据如何在磁盘中高效存取的就是DBMS数据库.
二、数据如何在磁盘中存储
现在假设我们有一张数据表, employee表. 假设各个字段长度如下, 加起来刚好128字节. 意思就是表中的一行(一条记录)大小为128字节.
假如有100行数据, 共12800字节,每个块能存512字节,那就需要25个块.
4行记录刚好512字节,一个块。

三、索引
为了快速查找到底是哪25个块记录着这些数据,我们要给数据建立索引。索引由employee表的id作为查找key,value是一个指向哪个block的指针。
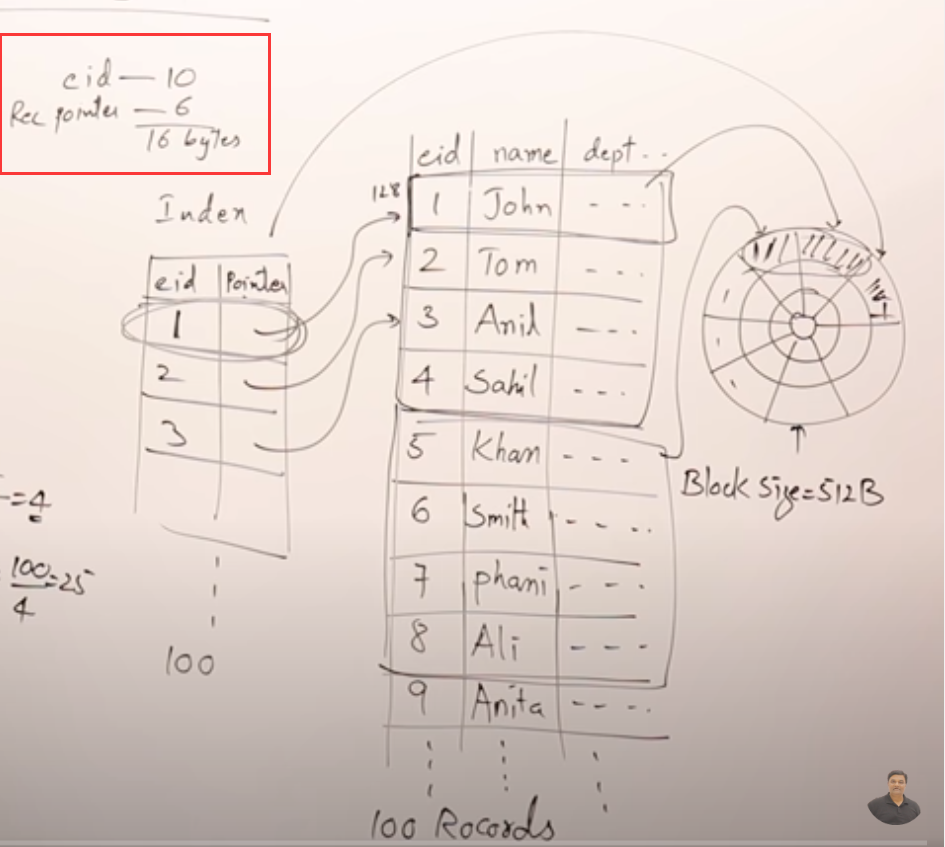
索引也是数据,也得存磁盘里。也就是它也得存到block里。假设一行索引16字节。那么32条数据占一个block,100条数据占3.2个块四舍五入4个block。
那么查找一个数据,先在索引里找,最多需要查4个block,完了从数据里查,直接通过索引能查到一个block,一共读了5个block,比直接在数据里查25个block少了很多。
四、多级索引
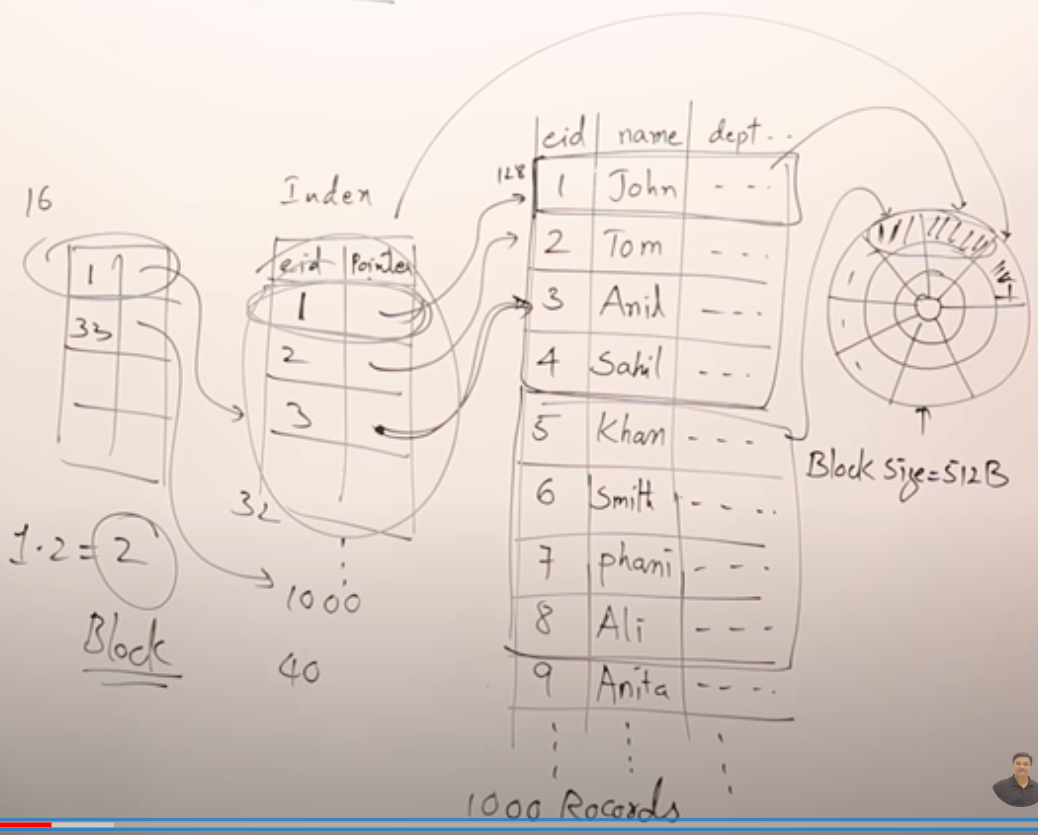
如果有1000条数据,之前100条数据,它的索引占了4个block,那1000条数据的索引就占了40个block(随便算的,并不严谨)。
为了更快查找,我们可以给这40个block也简历索引,就是多级索引了,暂时称为二级索引吧。二级索引的第一条记录,指向一级索引的第一个block(32行),
一级索引一共有占据40个block,那么二级索引就一共有40行,32行占一个字节,40/32,二级索引一共只占1.2约等于2个block。
查找时,二级(2个block)->一级(1个block)->数据(1个block),大大缩减了查找时读取磁盘块的数量。
五、M-路搜索树
多级索引,就是一层一层的对数据、索引所在的block进行指针指向,它看起来已经很像树型结构了。但我们需要的是一共能够自我调整(增加级数、减少级数)的树。
回忆一下二叉搜索树,一个节点中只有一个数字(一个key),按照左小右大,它有两个孩子。
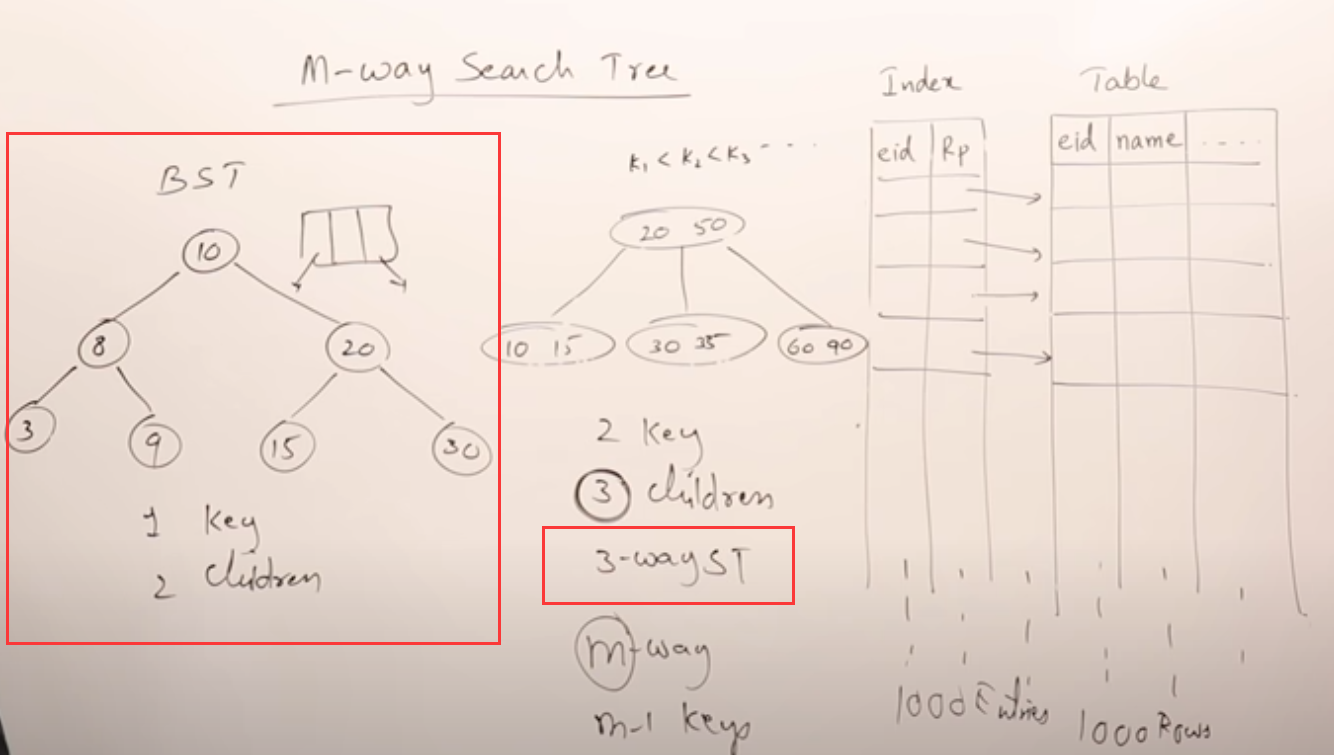
m-way搜索树,每个节点中有m-1个key,由小到大k1<k2<...<km-1,它可以有m个孩子,思想和二叉搜索树一样,比key小的在key的左分支,比key大的在key的右分支。
一个4-way搜索树的节点内部结构如下。
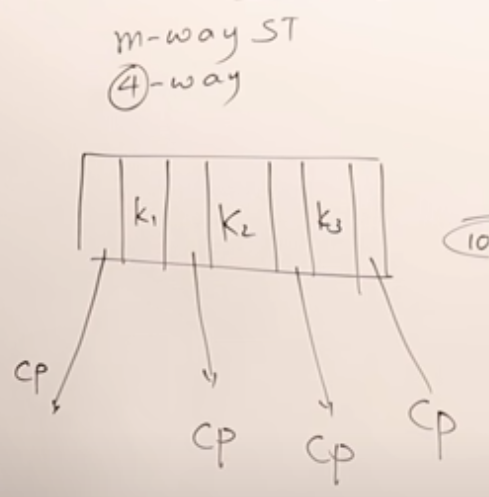
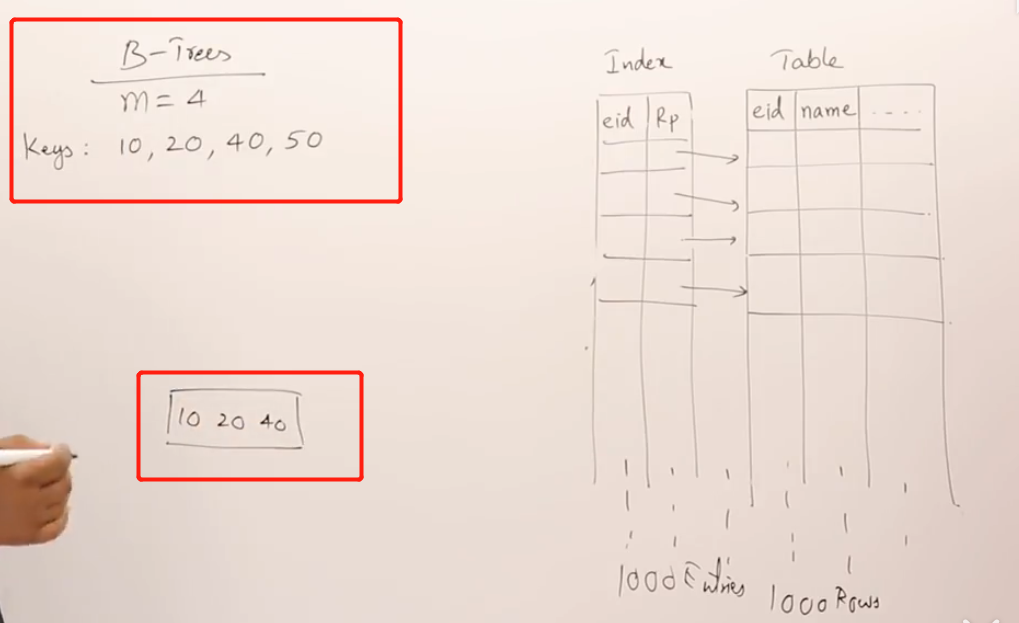
这种m-way搜索树可以用来存索引吗?可以,比如下面这个4路的,Rp是指向表中数据所在位置的指针。
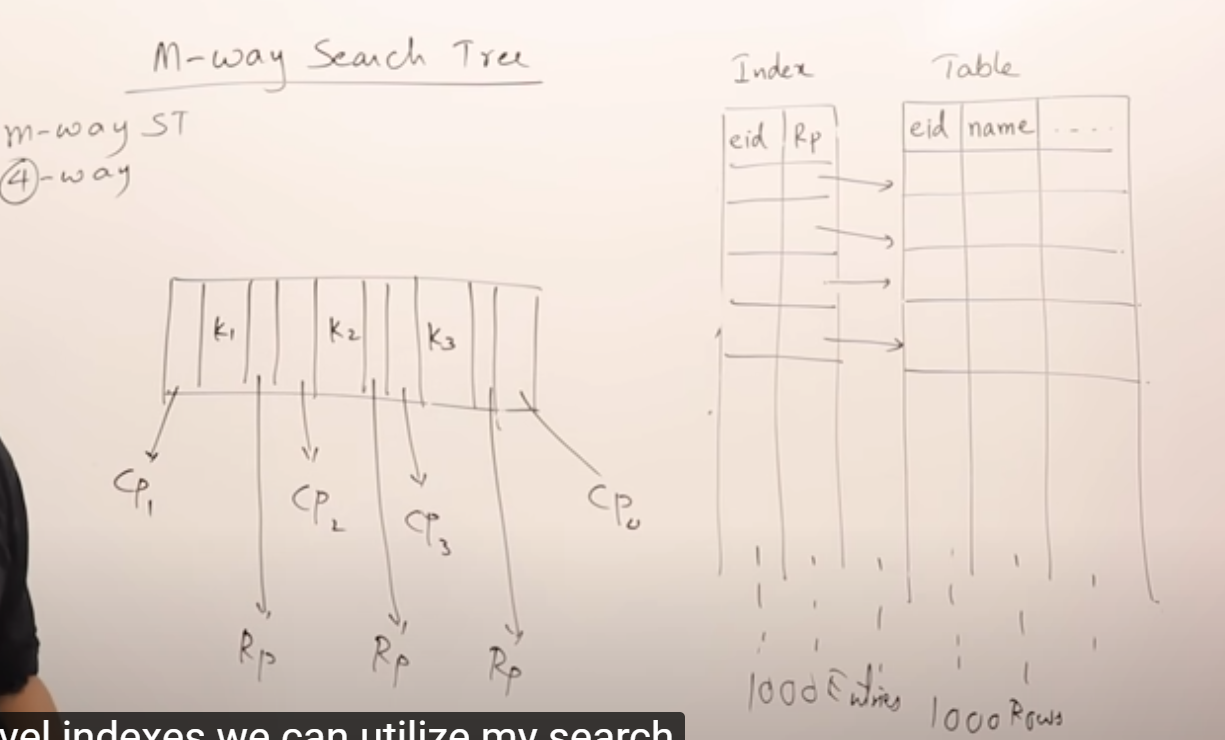
但是m-way搜索树有些问题,第一,因为它的定义简单(类似二叉搜索树),直接按照定义来插入数据,会产生不平衡的树。比如一个度为10的m-way搜索树,
本来一个节点能放9个key,但是直接插入的话,它就成了单边树。

第二它不能自我管理。
六、B树
B树就是一棵m-way搜索树上增加了一些定义和限制条件。假设度为m(意思是一个节点最多有m个孩子)
1. 每个节点至少得有[m/2] (上取整)个子树;(此定义是用来控制树的高度,防止单边树产生)
2. 根节点最少可以有两个孩子(子树);(这条定义是用来特殊处理根节点的。假如没有此定义,整棵树都没法生成,新加入
的数据全得往子树里放,根节点的key加不进去。)
3. 所有叶子节点都在同一层;
4. 建立树是一个从底向上的过程;
七. B树的插入
下面是一个B树创建的例子,度为4,key最多为3.
插入10, 20, 40后, 50没地方放了。做法是开始分割节点,以分界点40作为父节点,10、20放一个节点,50放一个节点(这种分级点选择方法默认把较多数据放到节点左边)。
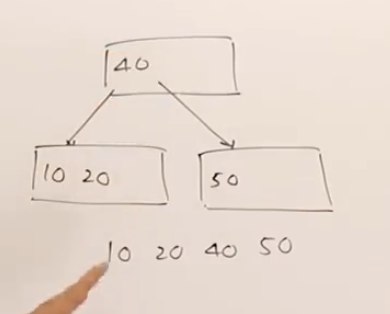
接着插入60, 70, 插入80的时候再次分割,并且把分界点70送到父节点中。
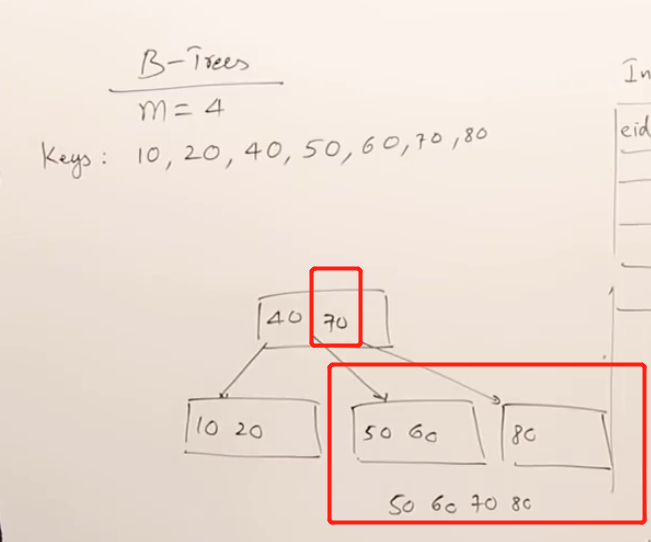
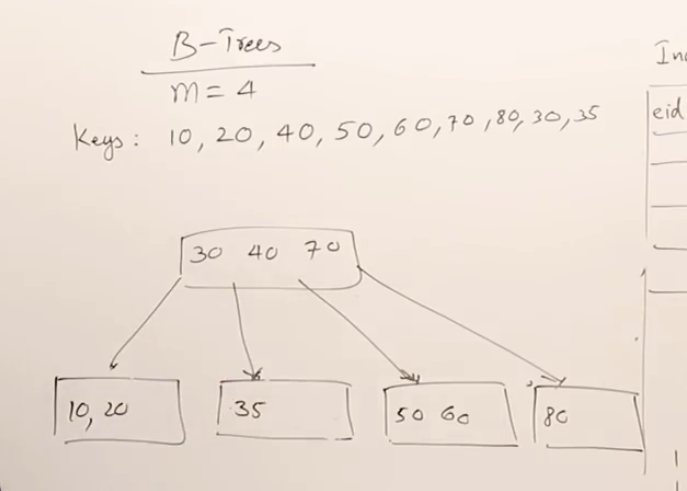
更够自动调整层高和节点大小的B树,其结构已经很像数据库的多级索引了,下图红框意思是指向数据的指针。节点里的key就是索引的id。
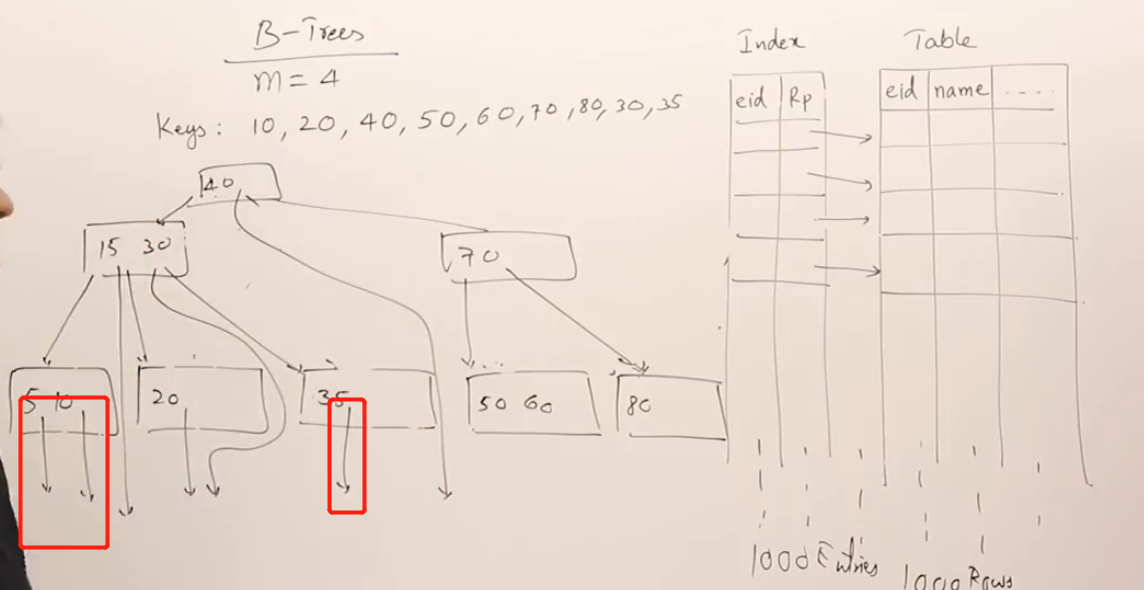
八、B+树
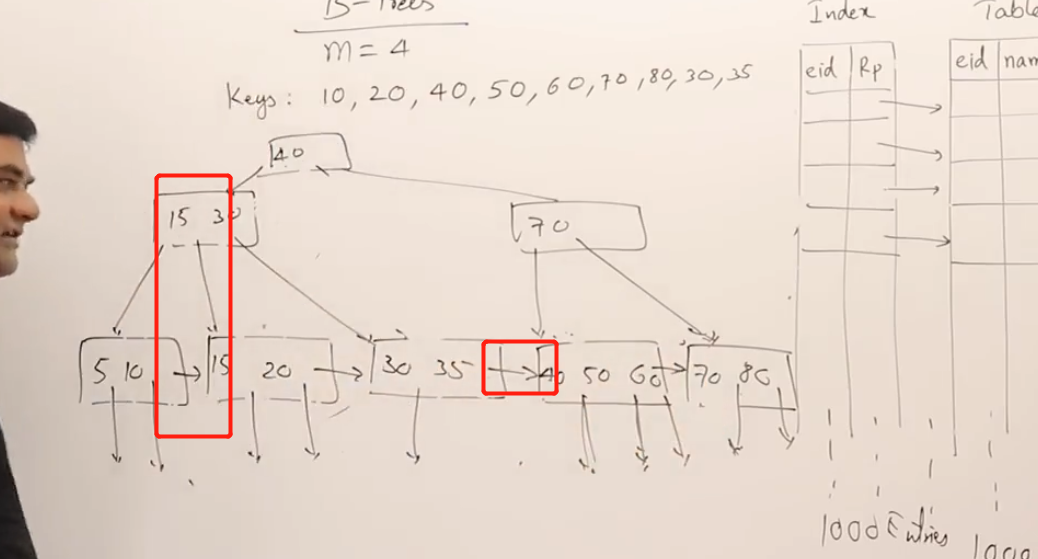
1. B树中,所有节点都有指向索引地址的指针。B+树中只有叶子节点有这种指针。
2. B+树中,叶子节点中会有其根节点的一份copy,
3. 叶子节点互相连接;
4. B+树的结构更像多级索引,只有一级索引上有连接至数据地址的指针。
只有第一级索引是dense的,其他高级索引是sparse的。
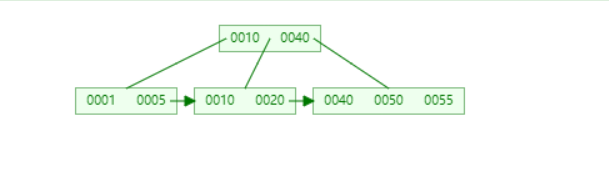
这是两个B树和B+树在线可视化过程的链接
https://www.cs.usfca.edu/~galles/visualization/BTree.html
https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html