Legend
Link \(\textrm{to LOJ}\)。
original
你有 \(m\ (1 \le m \le 23)\) 个信号站,你可以任意安排它们之间的顺序。
再给定一个长度为 \(n\ (1 \le n \le 10^5)\) 的数组 \(S\) 表示信号站之间要进行 \(n-1\) 次通讯,分别是 \(S_i \to S_{i+1}\ (i <n)\)。如果两个分别位于 \(a,b\) 号位置上的信号塔要进行 \(a\to b\) 传输,那么根据限制条件只能使用两种通讯方式之一:
- 若 \(a\le b\),花费 \(b-a\)的代价传输。
- 若 \(a >b\),花费 \(k(b+a)\) 的代价传输,\(k\ (1 \le k \le 100)\) 为给定常数。
请求出最优情况下代价的最小值。
simplified
给定一个 \(m\times m\ (1 \le m \le 23)\) 的二维数组 \(v\ (\sum v \le 10^5-1)\)。和一个常数 \(k\ (1 \le k \le 100)\)。对于一个 \(1\sim m\) 的排列 \(p\),我们可以求出它的花费为:
请求出最优情况下花费的最小值。
Editorial
作为 联合省选2020 的第四题,是一道良心送温暖题,这个套路我在冲刺 \(\textrm{TG}\) 组的时候就有所耳闻,让我们一起为出题人点赞。
fake solution
\(m\) 出乎意料的小,于是考虑状压。
一种很 \(\textrm{naive}\) 的想法是设 \(dp_{st}\) 表示从左到右 \(\textrm{bitcount(st)}\) 个信号站已经放了 \(st\) 集合里的所有信号站。转移直接枚举一个新信号站,加上别人到他的贡献(第一种传输)和他到前面的贡献(第二种传输)。
但你发现这两种贡献不好保存计算,因为你必须知道他们之间的距离,而在这个数据范围下是不可以状压的。
这意味着不能加入一个信号站的时候计算所有与它相关的贡献,以上 \(\textrm{dp}\) 转移假了。
山重水复疑无路。
real solution
part 1
不妨我们只考虑第一种传输,即只有从左往右的。
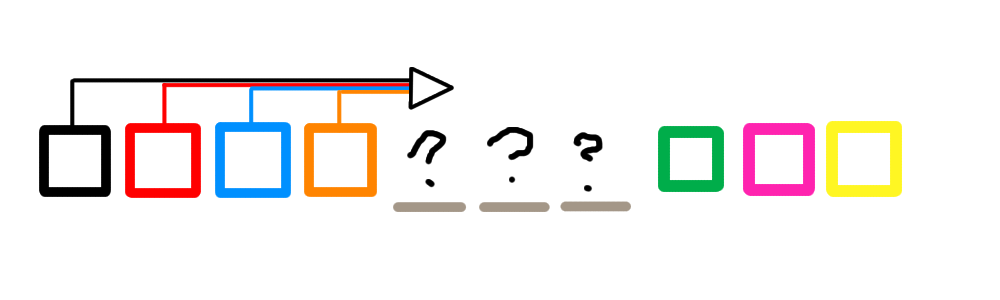
假设我们有 \(黑 \to 绿\) 的一条传输,那么只要 \(绿\) 没有出现,\(黑\) 出现了,就一直会造成贡献。也就是每放一个新信号塔,只要 \(绿\) 没出现,那么就会造成 \(1\) 的贡献,造成的总贡献就是它们之间的距离。
那么就说明每一对 \((\)出现过的,没出现的\()\),且有传输要求的都会在放置一个新的信号塔后产生 \(1\) 的贡献。
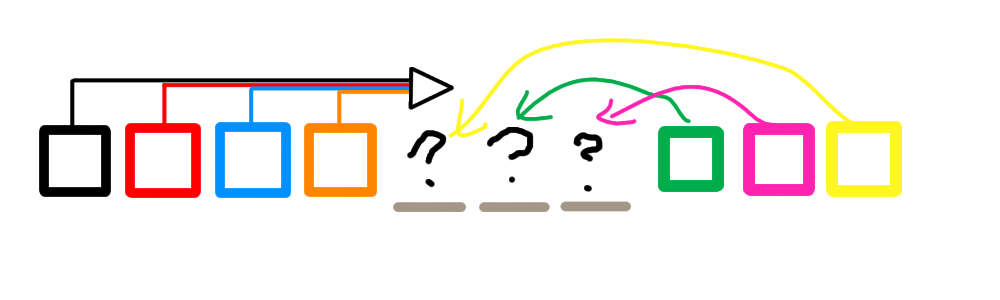
由上图来看,我们就根本不需要记录他们的出现位置了。
part 2
再考虑从第二种传输方法。我们把它拆成两部分:
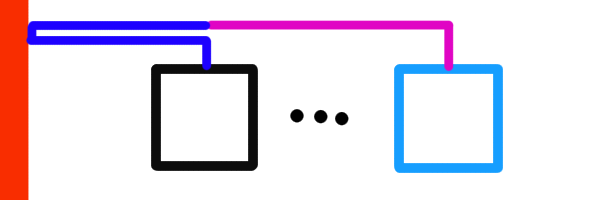
右半部分紫色的贡献可以直接与 \(\textrm{part 1}\) 同时计算。
左半部分蓝色的贡献直接在加入新信号塔的时候计算。
Code
代码不算太难,主要要预处理以下东西:
- \(cb_{st}\) 表示当前放了 \(st\) 集合的信号塔,如果放一个新的,造成的 \(\textrm{part 1}\) 代价与 \(\textrm{part 2}\) 蓝色部分线路代价之和。
- 枚举当前选了哪一个既可以转移,复杂度 \(O(2^mm)\)。
- \(cf_{i,st}\) 表示当前放了 \(st\) 集合的信号塔,如果下一个放 \(i\) 信号塔,造成的 \(\textrm{part 2}\) 蓝色线路有多少次单程路线。
- 为什么要这么记呢,因为我们没有办法记录总长度。但因为左半部分蓝色的贡献直接在加入新信号塔的时候计算,这个时候蓝色单程的长度是确定的,所以乘上 \(k\) 和路线长度就可以了。
- 容易发现 \(cf\) 数组直接开是开不下的。\(st\) 的集合相互之间没有影响,所以可以把集合拆成两个小集合,变成 \(cf1_{i,st}\) 和 \(cf2_{i,st}\),分开算贡献。
- 复杂度 \(O(2^{\frac{m}{2}}m^2)\)。
\(dp\) 复杂度是 \(O(2^mm)\),所以总复杂度 \(O(2^mm)\),可以稳稳当当通过此题。
空间复杂度 \(O(2^m+m^2)\),可以稳稳当当通过此题。
// Author : Imakf
#include <bits/stdc++.h>
#define int unsigned
int read(){
char k = getchar(); int x = 0;
while(k < '0' || k > '9') k = getchar();
while(k >= '0' && k <= '9')
x = x * 10 + k - '0' ,k = getchar();
return x;
}
void cm(int &a ,int b){a = a < b ? a : b;}
const int MX = 23;
int cnt[MX][MX];
int lg2[1 << MX];
int dp[1 << MX];
int cb[1 << MX];
// 考虑以这个状态新放一个,消耗的普通传递代价以及特殊传递的前半段代价
int cf1[23][1 << 12] ,cf2[23][1 << 12];
// 考虑以这个状态新放一个 i,i 要造成多少次特殊传递
const int base = (1 << 12) - 1;
signed main(){
int n = read() ,m = read() ,k = read();
for(int i = 0 ,last = -1 ,now ; i < n ; ++i ,last = now){
now = read() - 1;
if(~last) ++cnt[last][now];
}
for(int i = 0 ; i < m ; ++i) cnt[i][i] = 0 ,lg2[1 << i] = i;
for(int i = 1 ; i < 1u << m ; ++i){
int add = lg2[i & -i];
cb[i] = cb[i ^ (i & -i)];
for(int j = 0 ; j < m ; ++j){
if((i >> j) & 1) cb[i] -= cnt[j][add] + k * cnt[add][j];
else cb[i] += cnt[add][j] + k * cnt[j][add];
}
}
for(int i = 0 ; i < 1 << 12 ; ++i){
for(int j = 0 ; j < m ; ++j){
for(int s = 0 ; s < 12 ; ++s){
if((i >> s) & 1) continue;
cf1[j][i] += cnt[s][j];
}
for(int s = 12 ; s < m ; ++s){
if((i >> (s - 12)) & 1) continue;
cf2[j][i] += cnt[s][j];
}
}
}
for(int i = 1 ; i < 1u << m ; ++i){
int cnt1 = 0 ,cpi = i;
while(cpi) cpi -= cpi & -cpi ,++cnt1;
dp[i] = UINT_MAX;
for(int j = 0 ; j < m ; ++j){
if(((i >> j) & 1) ^ 1) continue;
cm(dp[i] ,dp[i ^ (1 << j)]
+ cb[i ^ (1 << j)]
+ (cf1[j][i & base] + cf2[j][i >> 12]) * cnt1 * 2 * k);
}
printf("%d\n" ,dp[(1 << m) - 1]);
return 0;
}