前序遍历
递归写法
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res, leftRes, rightRes;
if(root == nullptr)
return res;
res.push_back(root->val);
leftRes = preorderTraversal(root->left);
rightRes = preorderTraversal(root->right);
if(leftRes.size() > 0)
{
for(auto val : leftRes)
res.push_back(val);
}
if(rightRes.size() > 0)
{
for(auto val : rightRes)
res.push_back(val);
}
return res;
}
};

递归写法的时间复杂度,空间复杂度较为一般。
非递归写法
使用非递归写法时需要用到栈,这里采用了LC题解中一种不错的解法.
思路:带有nullptr标记的节点直接访问节点值,没有标记则对节点本身添加标记并遍历子节点,该过程用栈实现
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
if(root == nullptr)
return res;
stack<TreeNode*> nodes;
nodes.push(root);
while(nodes.size() > 0){
TreeNode* nowNode = nodes.top();
nodes.pop();
if(nowNode != nullptr){
// 右
if(nowNode->right != nullptr)
nodes.push(nowNode->right);
// 左
if(nowNode->left != nullptr)
nodes.push(nowNode->left);
// 根
nodes.push(nowNode);
nodes.push(nullptr);
}
else{
res.push_back(nodes.top()->val);
nodes.pop();
}
}
return res;
}
};

这个题解的优点在于只需要交换 //右,//左,//根三部分的顺序即可实现先序/中序/后序遍历方式,非常方便.
下图是一个遍历过程图示,可以更清晰地看到遍历过程。
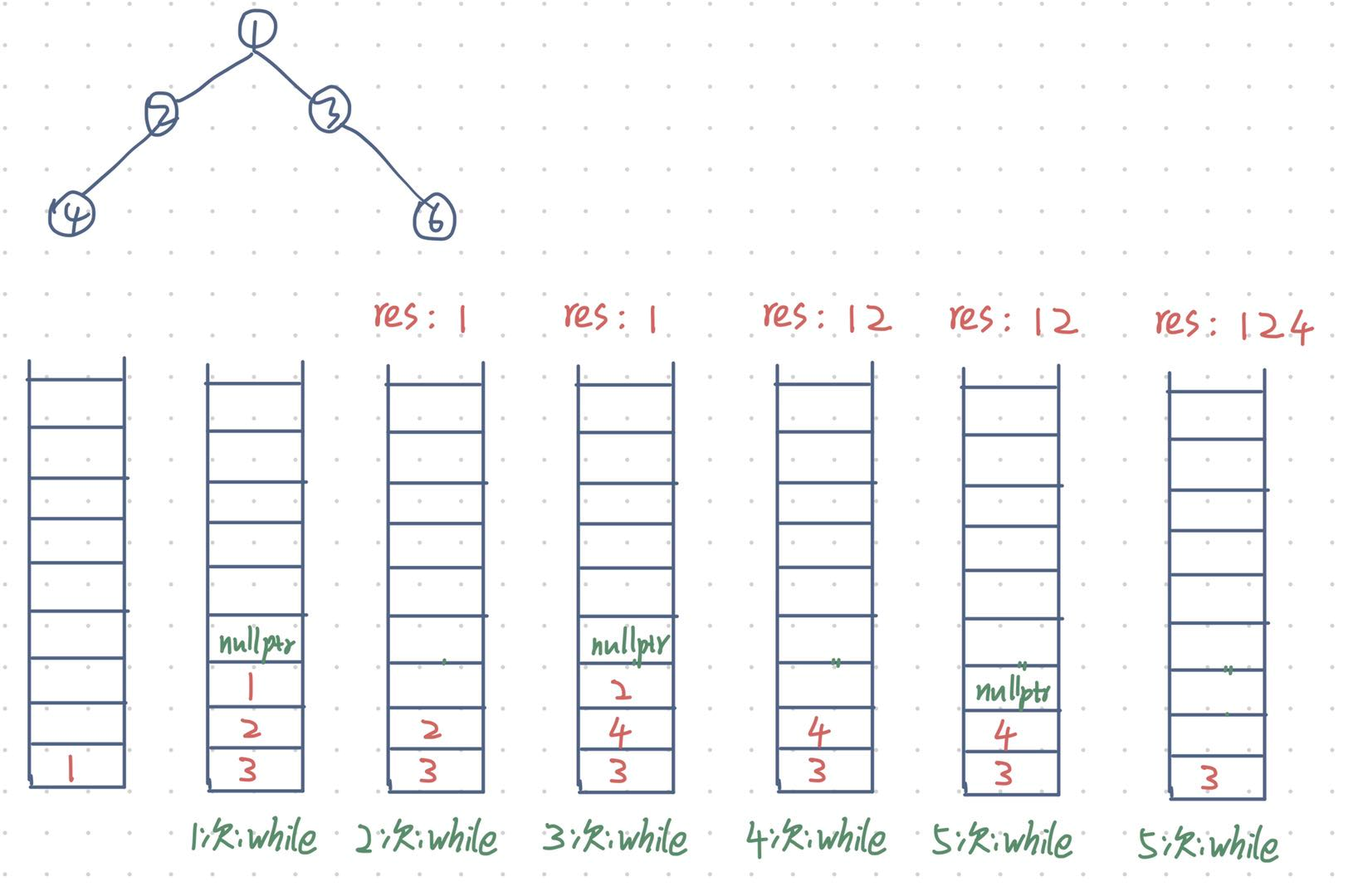
中序遍历
递归写法
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res, leftRes, rightRes;
if(root == nullptr)
return res;
leftRes = inorderTraversal(root->left);
rightRes = inorderTraversal(root->right);
if(!leftRes.empty()){
for(auto val : leftRes)
res.push_back(val);
}
res.push_back(root->val);
if(!rightRes.empty()){
for(auto val : rightRes)
res.push_back(val);
}
return res;
}
};

非递归写法
参考前序遍历的非递归写法即可
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
if(root == nullptr)
return res;
stack<TreeNode*> nodes;
nodes.push(root);
while(!nodes.empty()){
TreeNode* nowNode = nodes.top();
nodes.pop();
if(nowNode != nullptr){
// 右
if(nowNode->right != nullptr)
nodes.push(nowNode->right);
// 根
nodes.push(nowNode);
nodes.push(nullptr);
// 左
if(nowNode->left != nullptr)
nodes.push(nowNode->left);
}
else{
res.push_back(nodes.top()->val);
nodes.pop();
}
}
return res;
}
};

后序遍历
递归
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res, left, right;
if(root == NULL)
return res;
left = postorderTraversal(root->left);
right = postorderTraversal(root->right);
for(auto iter = left.begin(); iter != left.end(); iter ++)
res.push_back(*iter);
for(auto iter = right.begin(); iter != right.end(); iter ++)
res.push_back(*iter);
res.push_back(root->val);
return res;
}
};
非递归
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
if(root == nullptr)
return res;
stack<TreeNode*> nodes;
nodes.push(root);
while(!nodes.empty()){
TreeNode* nowNode = nodes.top();
nodes.pop();
if(nowNode != nullptr){
// 根
nodes.push(nowNode);
nodes.push(nullptr);
// 右
if(nowNode->right != nullptr)
nodes.push(nowNode->right);
// 左
if(nowNode->left != nullptr)
nodes.push(nowNode->left);
}
else{
res.push_back(nodes.top()->val);
nodes.pop();
}
}
return res;
}
};