bit operations
-
/2, *2
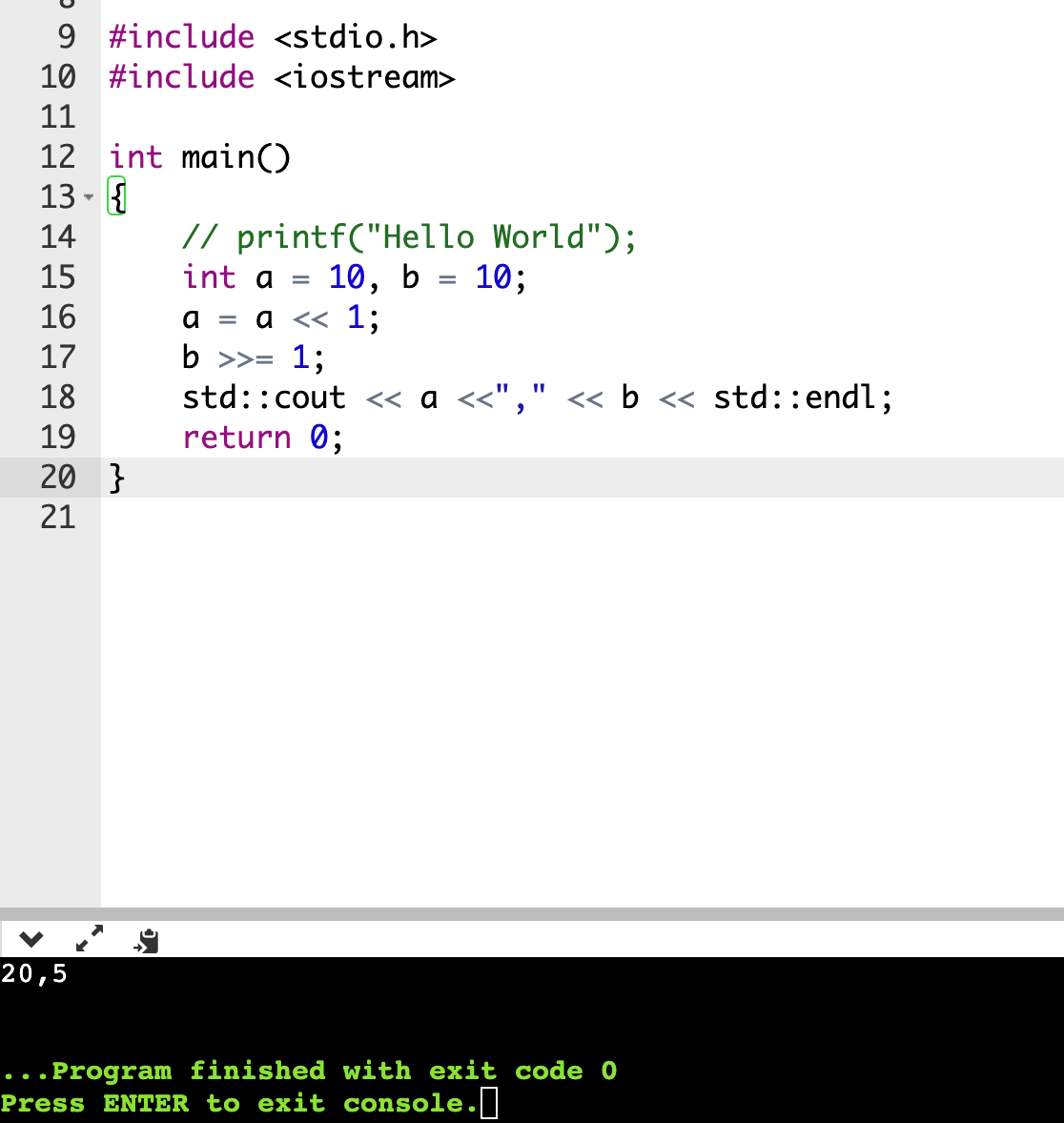
-
odd or even
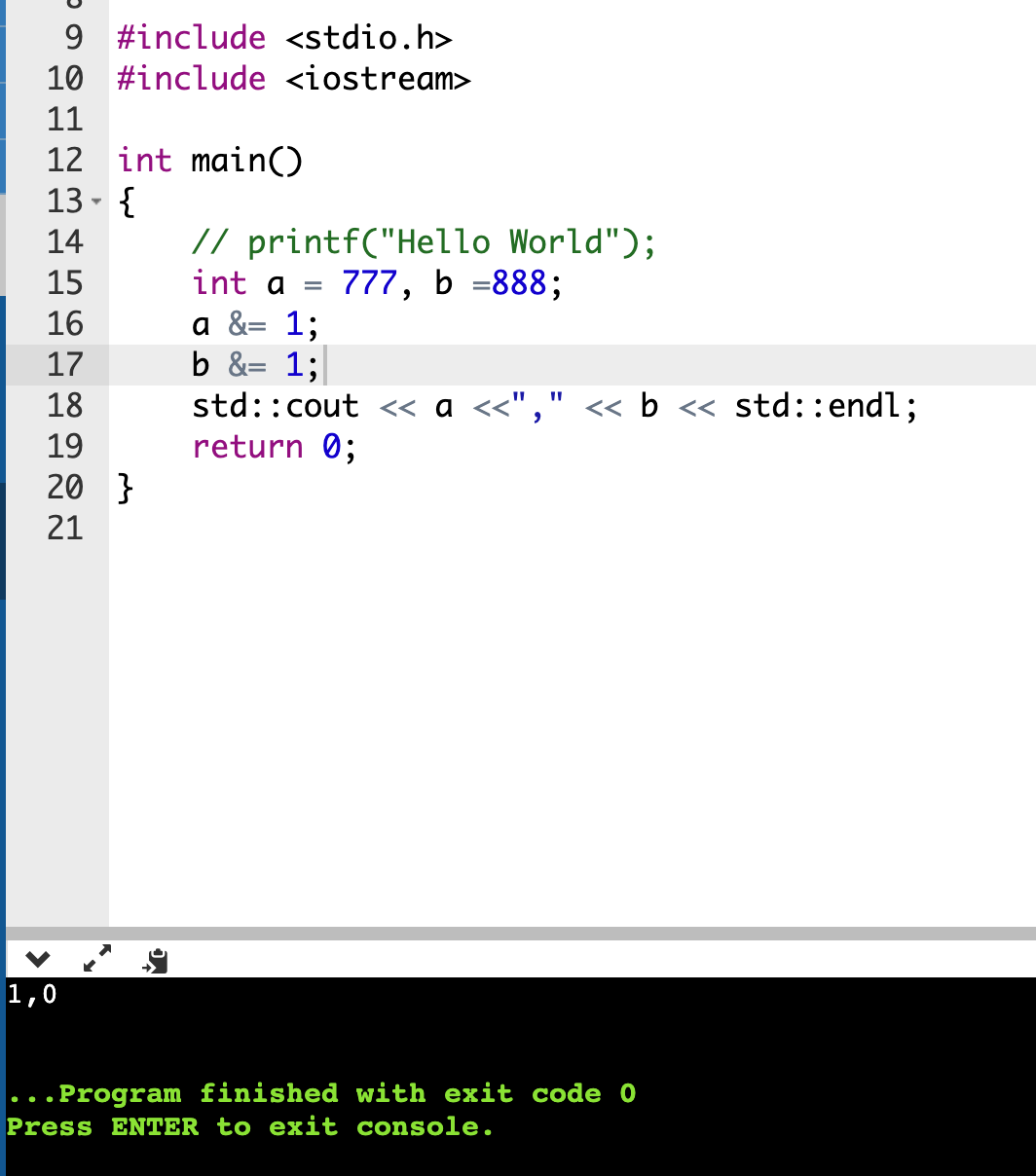
-
实现mod
当计算\(a \mod b\) 且 b是\(2^n\)时,可以直接使用\(a \& (b-1)\)来计算\(a \mod b\)。
原理为:$a \mod b \(是\)a/b$的余数。
因为\(b=2^n\),\(a/2^n\)又可以转换为
a=a>>n;所以$ a \mod b $ =
a - (a//b)*b= \(a - (a//2^n)*2^n\)所以\(a \mod b\) = a -
(a>>n)<<n又因为right shift是截断的,所以
(a>>n)<<n的结果是将a的低n位置0,记为\(a'\)所以\(a - a' = a + (-a') = a + ( \sim a'+1)\)
-
关于\(a - a'\) = 低n位的推导
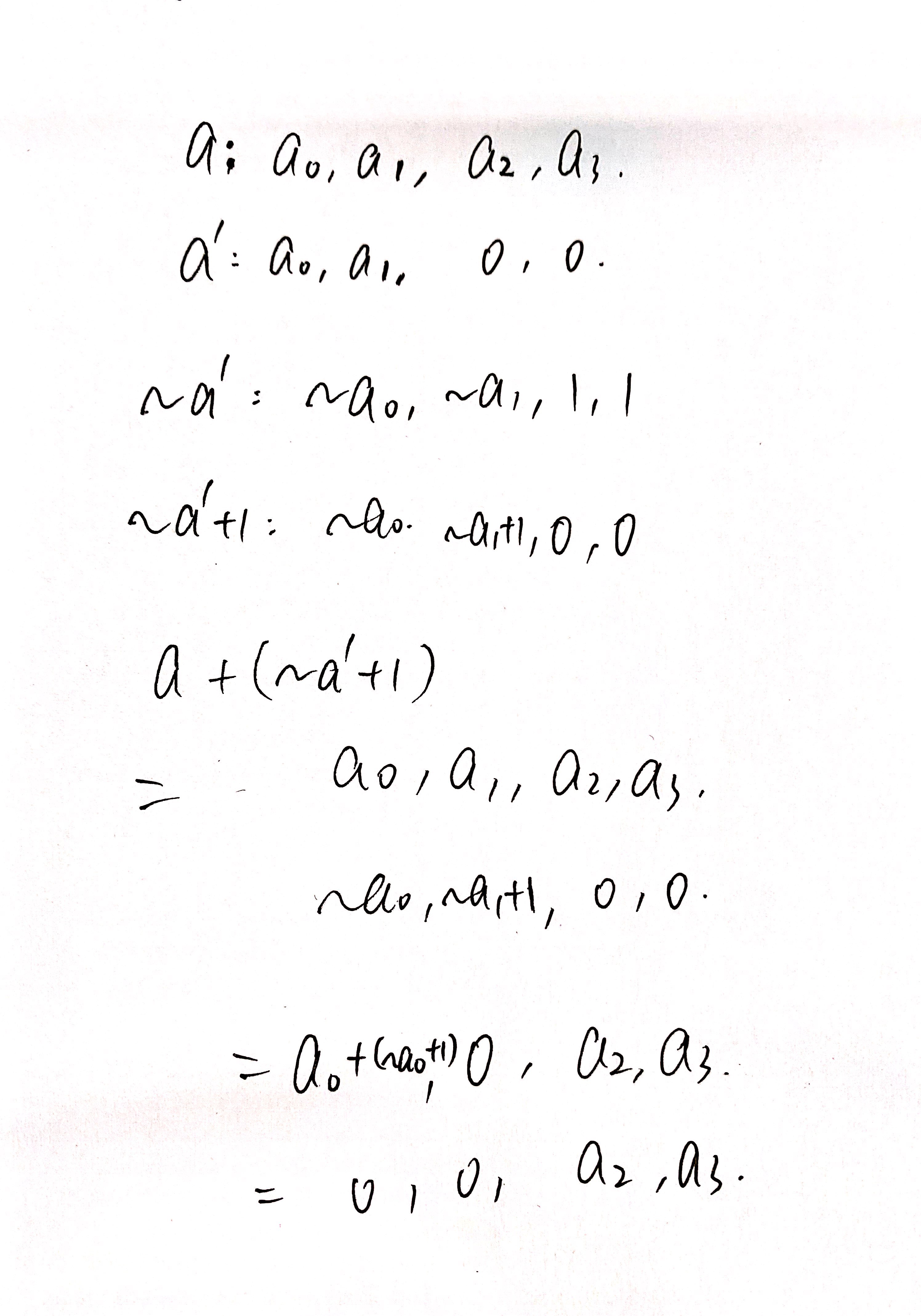
-
综上,可以得到结论:这个低n位就是mod运算的结果(余数)
所以,\(b-1=2^n-1\),二进制表示为n-1位全1
所以,\(a\&(b-1)\)就是取a的低n位,就是余数,即mod运算结果
-
求商
经过上面的推导,发现计算\(a \mod b\)当\(b=2^n\)时,a的低n位是余数,高m-n位是商。高m-n位是商的原因是:商应为\(a//b = a//2^n\) = a右移n位后的值,当a是正数时,符号位扩展一直是0,所以商是a的高m-n位。所以在这种情况下,求商的方法就是取a的高m-n位,之前取a的低n位操作是
a&(b-1),那么现在就是a&~(b-1)。这个操作可以在ispc的tutorial中看到:https://ispc.github.io/perfguide.html