013-二叉树

二叉树的介绍

1. 二叉树的定义

二叉树是每个节点最多有两个子树的树结构。它有五种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左、右子树皆为空。

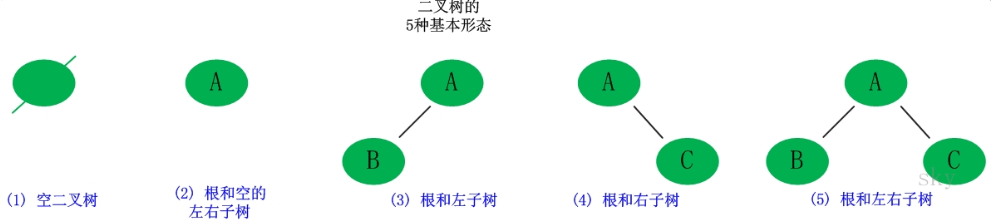
2. 二叉树的性质。

二叉树有以下几个性质：
性质1）：层次与层次上的节点数的不等关系式。设二叉树第i层的节点数为f(i)，则有：

            f(i) <= 2^{(i - 1)}。（其中i >= 1）。

性质2）：二叉树的高度h与二叉树节点总数f(h)的不等关系式。设二叉树的高度h，二叉树的节点总数为f(h)，则有：

            f(h) <= 2^h - 1。（其中h >= 1）。

性质3）：二叉树中度为2的个数为x与叶节点数f(x)的方程关系式。设二叉树中度为2的个数为x，页节点数为f(x)则有：

           f(x) = x + 1。（其中x >= 1）。

2.1 性质1：二叉树第i层上的结点数目最多为 2^{i-1} (i≥1)

证明：下面用"数学归纳法"进行证明。
        (01) 当i=1时，第i层的节点数目为2^{i-1}=2^{0}=1。因为第1层上只有一个根结点，所以命题成立。
        (02) 假设当i>1，第i层的节点数目为2^{i-1}。这个是根据(01)推断出来的！
               下面根据这个假设，推断出"第(i+1)层的节点数目为2^{i}"即可。
                由于二叉树的每个结点至多有两个孩子，故"第(i+1)层上的结点数目" 最多是 "第i层的结点数目的2倍"。即，第(i+1)层上的结点数目最大值=2×2^{i-1}=2^{i}。
                故假设成立，原命题得证！

 

2.2 性质2：深度为k的二叉树至多有2^{k}-1个结点(k≥1)

证明：在具有相同深度的二叉树中，当每一层都含有最大结点数时，其树中结点数最多。利用"性质1"可知，深度为k的二叉树的结点数至多为：
           2⁰+2¹+…+2^k-1=2^k-1
           故原命题得证！

 

2.3 性质3：包含n个结点的二叉树的高度至少为log₂ (n+1)

证明：根据"性质2"可知，高度为h的二叉树最多有2^{h}–1个结点。反之，对于包含n个节点的二叉树的高度至少为log₂(n+1)。

 

2.4 性质4：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1

证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)="0度结点数(n₀)" + "1度结点数(n₁)" + "2度结点数(n₂)"。由此，得到等式一。
         (等式一) n=n₀+n₁+n₂
　     另一方面，0度结点没有孩子，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是：n₁+2n₂。此外，只有根不是任何结点的孩子。故二叉树中的结点总数又可表示为等式二。
         (等式二) n=n₁+2n₂+1
        由(等式一)和(等式二)计算得到：n₀=n₂+1。原命题得证！

3. 满二叉树，完全二叉树和二叉查找树

3.1 满二叉树

定义：高度为h，并且由2^{h} –1个结点的二叉树，被称为满二叉树。

3.2 完全二叉树

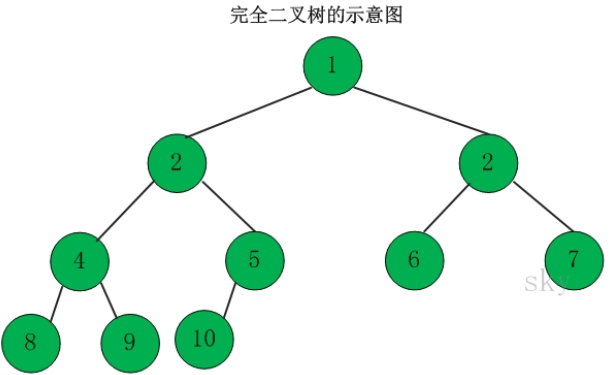
定义：一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

3.3 二叉查找树

定义：二叉查找树(Binary Search Tree)，又被称为二叉搜索树。设x为二叉查找树中的一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。

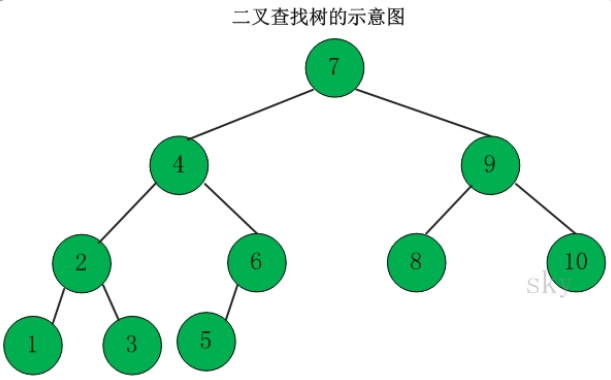
在二叉查找树中：
(01) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
(02) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点（no duplicate nodes）。

在实际应用中，二叉查找树的使用比较多。

4、二叉树遍历问题。

（1）先序遍历。（确定根节点）

   先访问这棵树的根，然后访问这棵树的左子树，再访问这棵树的右子树，最后递归访问左子树和右子树。

举例说明。如下图：

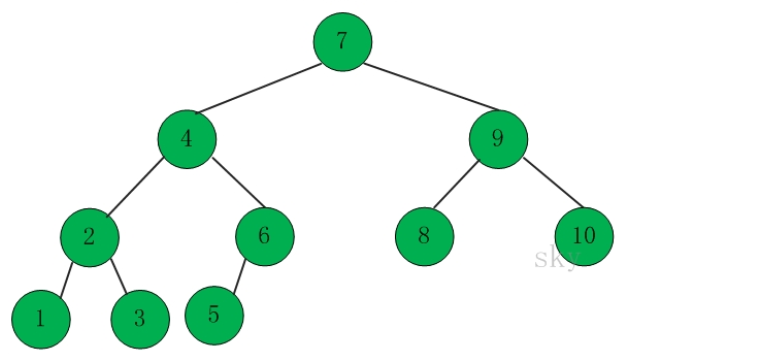
   根据先序遍历规则。这棵树的根是7，所以先序遍历是7，7的左子树的递归先序遍历，7的右子树的递归先序遍历。

因此先序遍历结果是：7，4，2，1，3，6，5，9，8，10

##############################################################

先序遍历：按照根节点->左子树->右子树的顺序访问二叉树

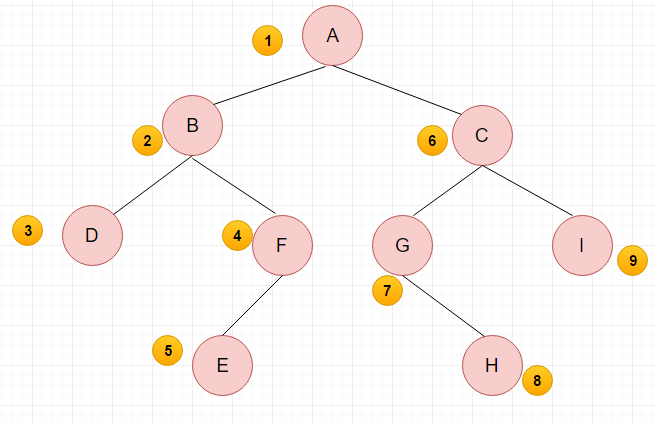
先序遍历：（1）访问根节点；（2）采用先序递归遍历左子树；（3）采用先序递归遍历右子树；

(注：每个节点的分支都遵循上述的访问顺序，体现“递归调用”)

先序遍历结果：A BDFE CGHI

思维过程：

（1）先访问根节点A，

（2）A分为左右两个子树，因为是递归调用，所以左子树也遵循“先根节点-再左-再右”的顺序，所以访问B节点，

（3）然后访问D节点，

（4）访问F节点的时候有分支，同样遵循“先根节点-再左--再右”的顺序,

(5)访问E节点，此时左边的大的子树已经访问完毕，

(6)然后遵循最后访问右子树的顺序，访问右边大的子树，右边大子树同样先访问根节点C,

(7)访问左子树G,

(8)因为G的左子树没有，所以接下俩访问G的右子树H,

(9)最后访问C的右子树I

（2）中序遍历。（知道根节点的情况下，可以确定根节点的左子树和右子树）

   先访问这棵树的左子树，然后访问这棵树的根，再访问这棵树的右子树，最后递归访问左子树和右子树。

 

举例说明。如下图：

 

 

   根据中序遍历规则。这棵树的根是7，所以中序遍历是7的左子树的递归中序遍历，7，7的右子树的递归中序遍历。

 

因此先序遍历结果是：1，2，3，4，5，6，7，8，9，10

 #############################################################

中序遍历：按照左子树->根节点->右子树的顺序访问

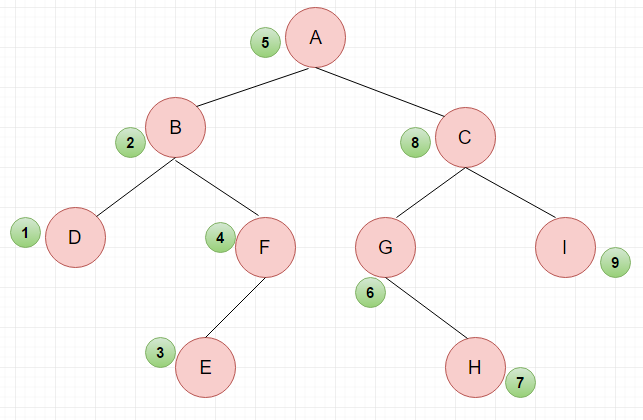
中序遍历：（1）采用中序遍历左子树；（2）访问根节点；（3）采用中序遍历右子树

 

中序遍历结果：DBEF    A    GHCI

（3）后序遍历。（确定根节点）

   先访问这棵树的左子树，然后访问这棵树的右子树，再访问这棵树的根，最后递归访问左子树和右子树。

 

举例说明。如下图：

 

 

   根据后序遍历规则。这棵树的根是7，所以后序遍历是：7的左子树的递归后序遍历，7的右子树的递归后序遍历，7。

 

因此后序遍历结果是：1，3，2，5，6，4，8，10，9，7

 ###################################################

后序遍历

 

 

后序遍历：（1）采用后序递归遍历左子树；（2）采用后序递归遍历右子树；（3）访问根节点；

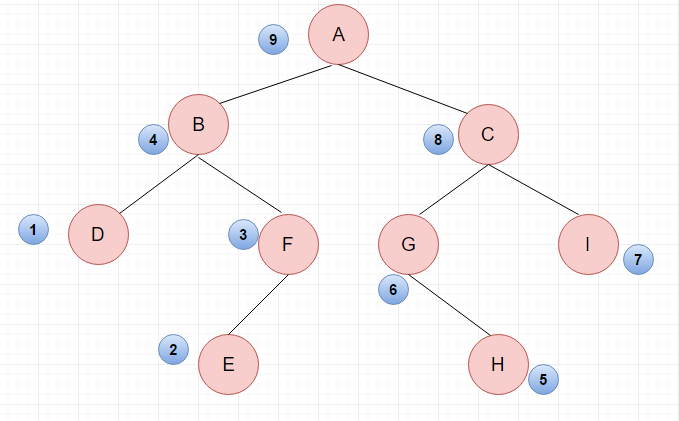
后序遍历的结果：DEFB  HGIC   A

（4）层次遍历。

   从根节点开始，一层一层地往下遍历。

（5）已知先序遍历和中序遍历求后序遍历，即确定二叉树。

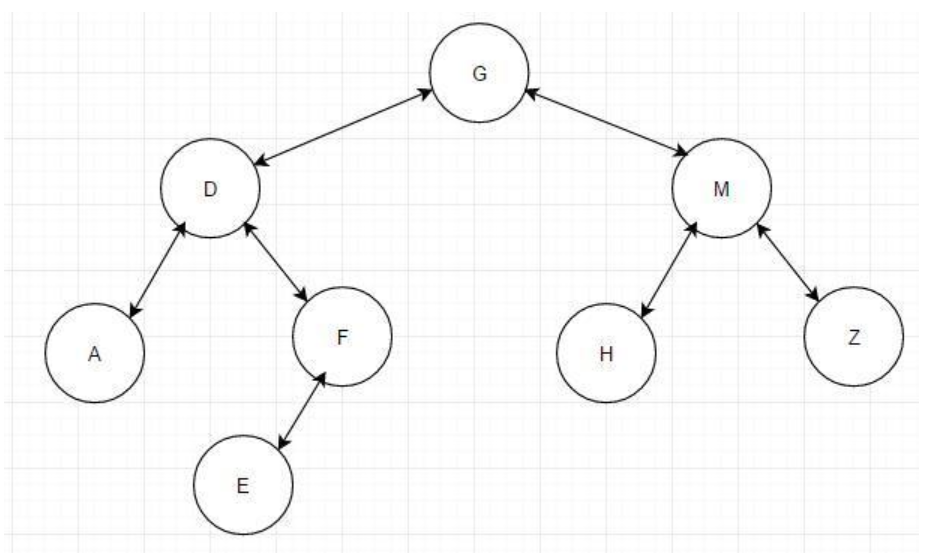
举例分析。先序遍历是:GDAFEMHZ。中序遍历是：ADEFGHMZ。求二叉树。

思路如下：（先确定根，再确定根的左子树，再确定根的右子树，然后递归左子树，然后递归右子树）
a、 根据先序遍历的特点——根左右，第一个元素一定是根节点，所以立刻确定G是根节点。
b、 既然确定了G是根节点，再根据中序遍历的特点——左根右，在根节点G之前的ADEF就是左子树，根节点G之后的HMZ就是右子树。
c、接着分析左子树（思路和第1，2步一样）。把左子树的所有元素（即ADEF这四个元素）在先序遍历和中序遍历中的顺序拿出来进行比较。
d、先序的顺序是DAFE（中左右），中序遍历是ADEF（左中右）。
e、通过先序特点得出D是左子树的节点，通过中序特点确定唯一一个在D左边的A是左子树中的左叶子，右边的是EF。
f、观察EF的相对位置，在先序（中左右）是FE，在中序（左中右）EF，所以得出EF的关系是左中。

g、接着分析右子树（思路和第1，2步一样），把右子树的元素（HMZ）在先序遍历和中序遍历中的顺序拿出来进行比较。
h、先序的顺序是MHZ（中左右），中序遍历是HMZ（左中右）。
i、根据先序遍历的特点确定M是右子树的节点，根据中序遍历的特点确定H是左叶，Z是右叶。

最后结果如下：那么后序遍历就是AEFDHZMG

 

 

 

 

   （6）已知后序遍历和中序遍历求先序遍历，即确定二叉树。

   （7）不能根据先序遍历和后序遍历确定中序遍历，即不能确定是唯一的二叉树。

举例说明：