0、递归定义。



1、递归的场景:

2、递归的基本思想就是把规模大的问题转化为规模小的相似的子问题来解决。特别地,在函数实现时,因为解决大问题的方法和解决小问题的方法往往是同一个方法,所以就产生了函数调用它自身的情况。
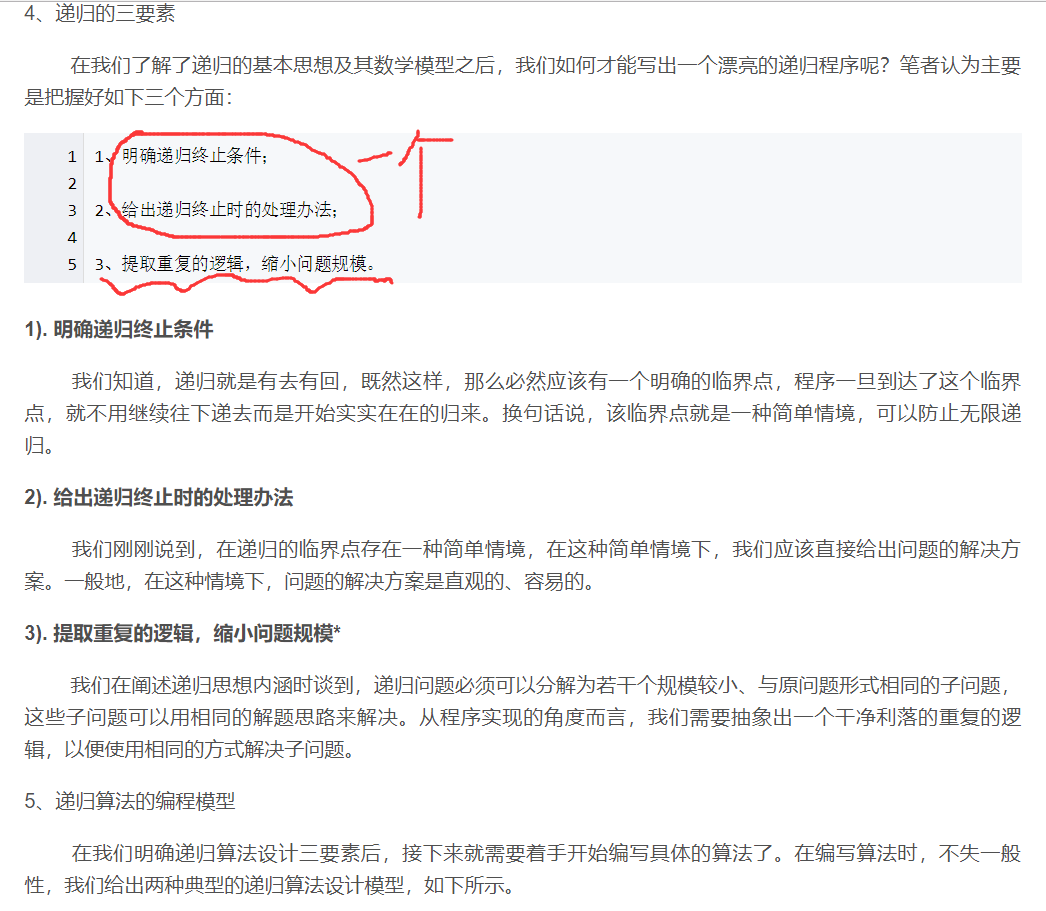

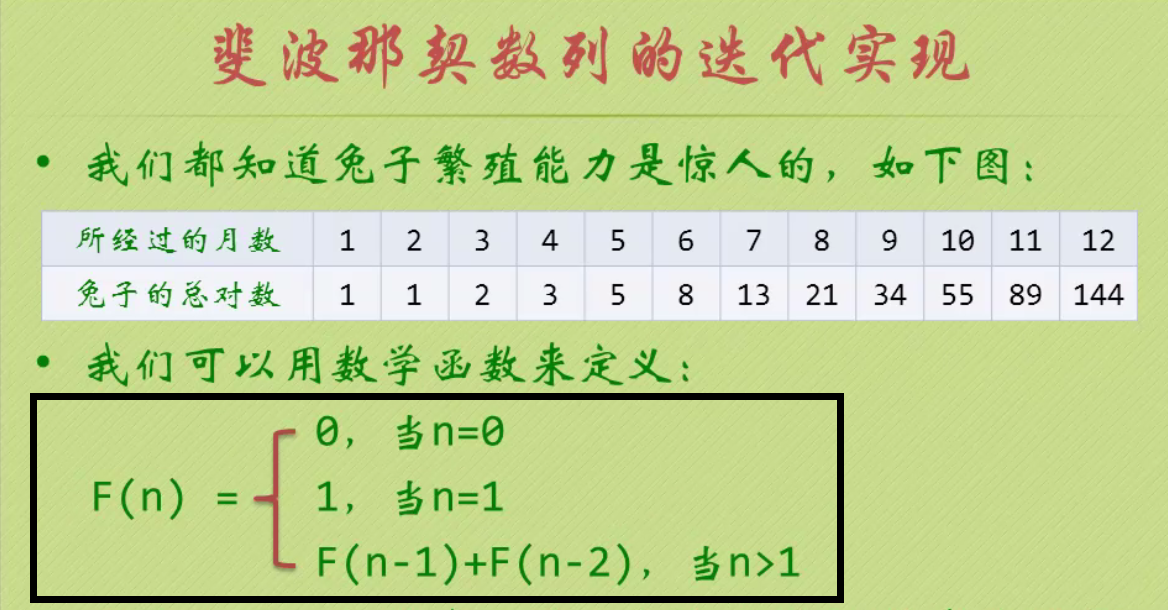
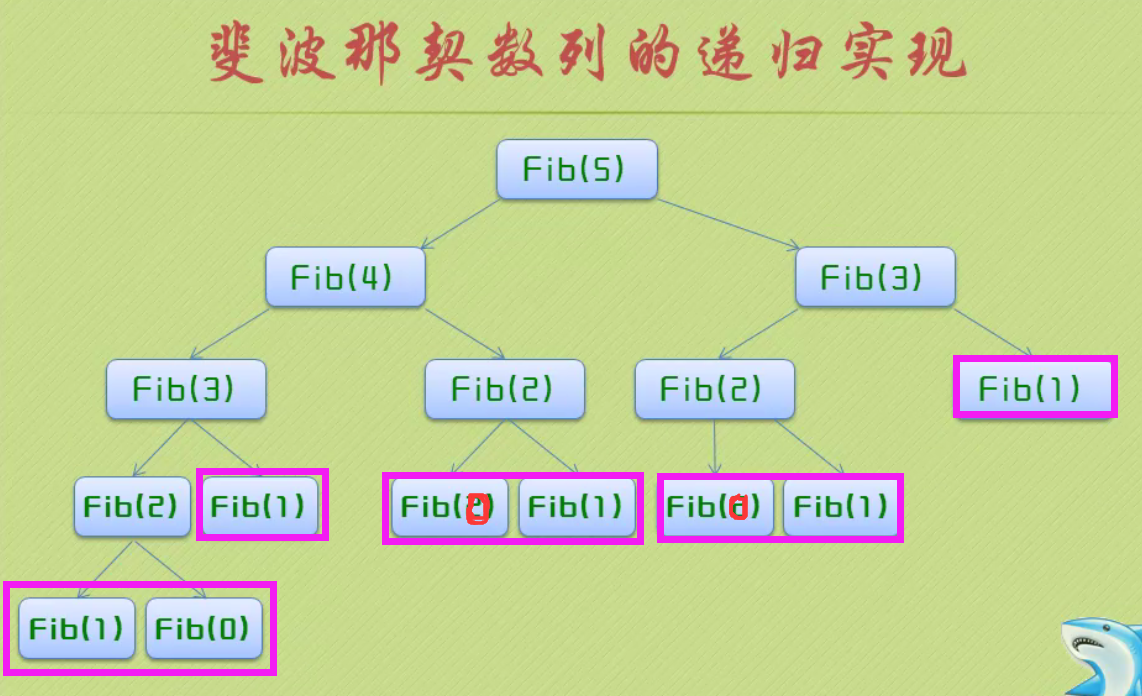
1)斐波纳契数列。



2)阶乘。

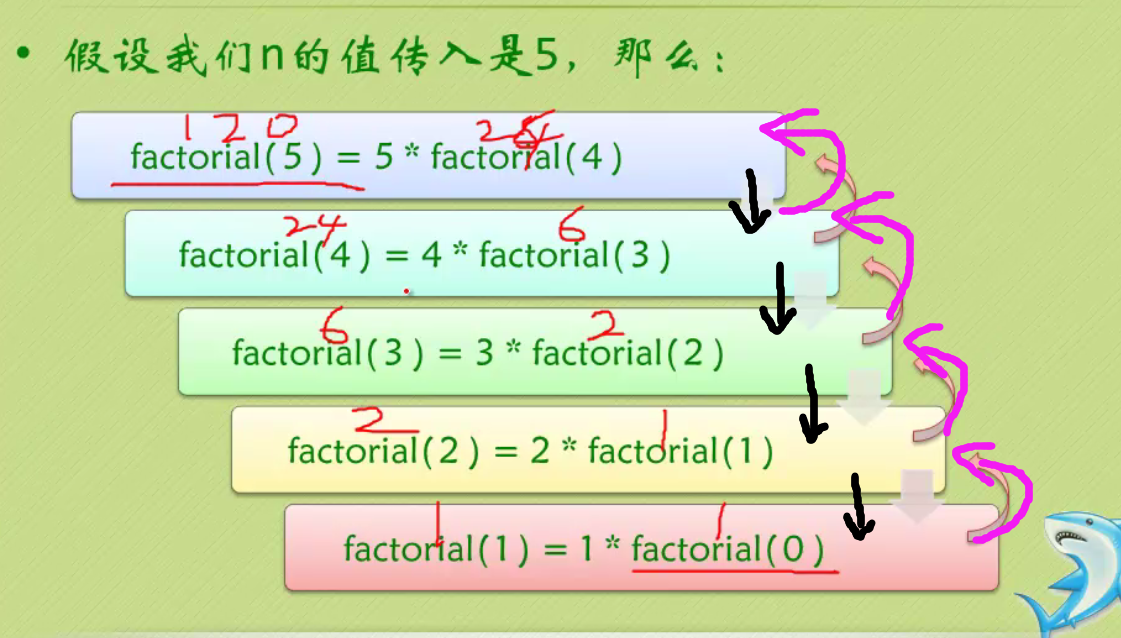
(1)原表达式“factorialFunction(n)”的含义是:求n的阶乘。
(2)问题转换为:求原表达式的等价表达式是:“factorialFunction(n - 1) * n”。(等价表达式要求:等价表达式的问题规模比原表达式的问题规模要小,且方法一样,只是参数的取值可能不同)
(3)求取等价表达式的最小问题规模:“n = 1 || n = 0”。即临界条件处理。

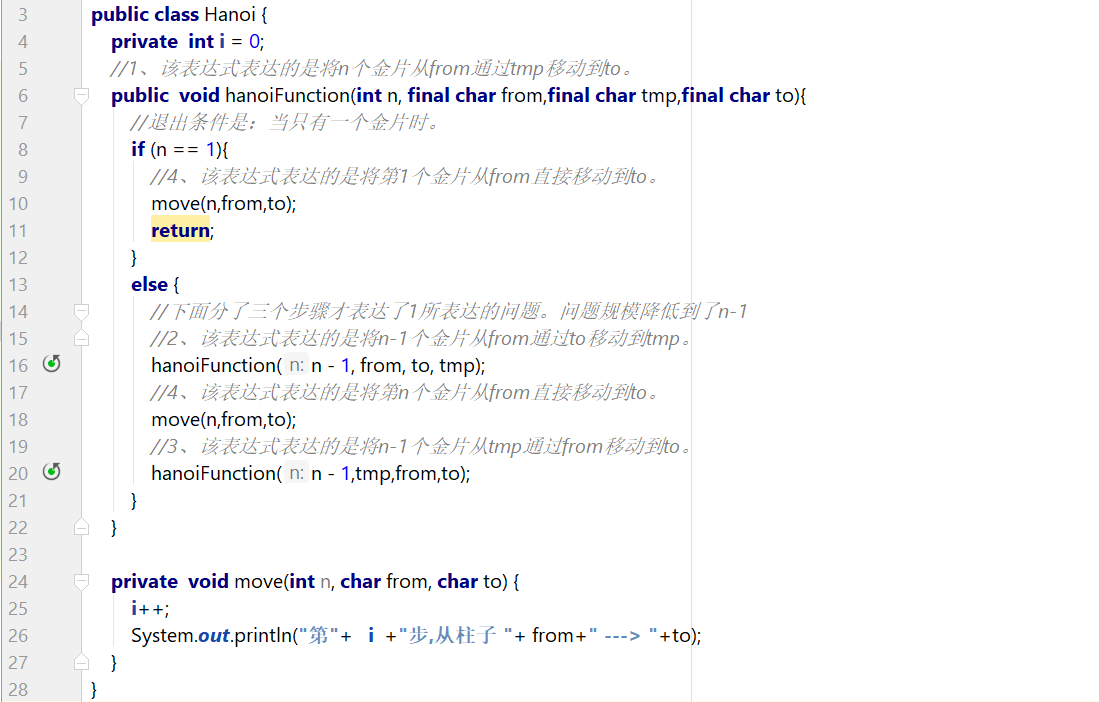
3)汉诺塔问题。


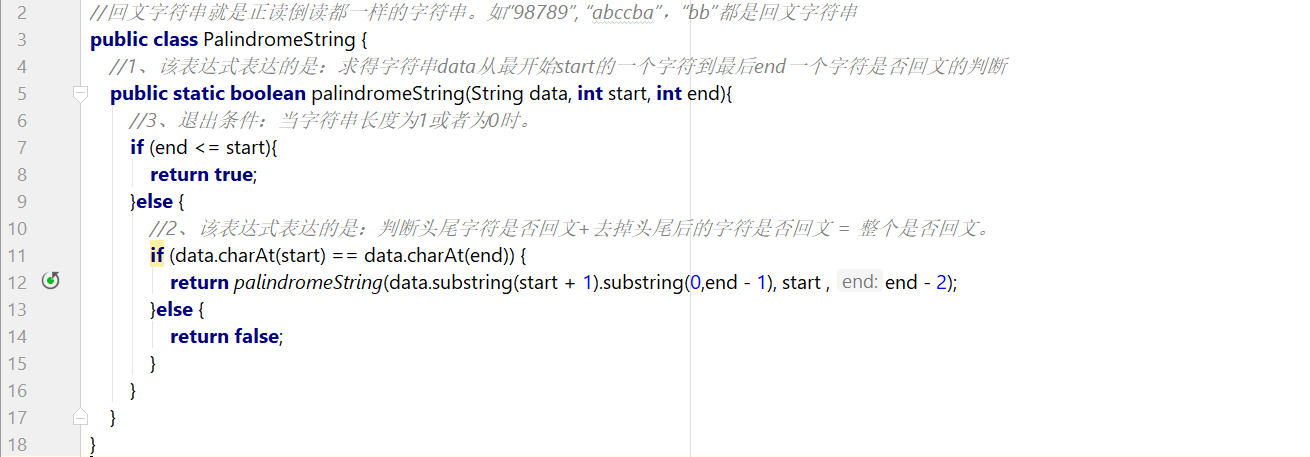
4)回文字符串问题。
5)全排列问题。

举例说明:求A、B、C、D的全排列。
问题转换为:“A、B、C、D的全排列”等价于
1、A在第一位时,B、C、D的全排列;
2、B在第一位时,A、C、D的全排列;
3、C在第一位时,A、B、D的全排列;
4、D在第一位时,A、B、C的全排列。
即“A、B、C、D的全排列”等价于上面这四种情况的之和。
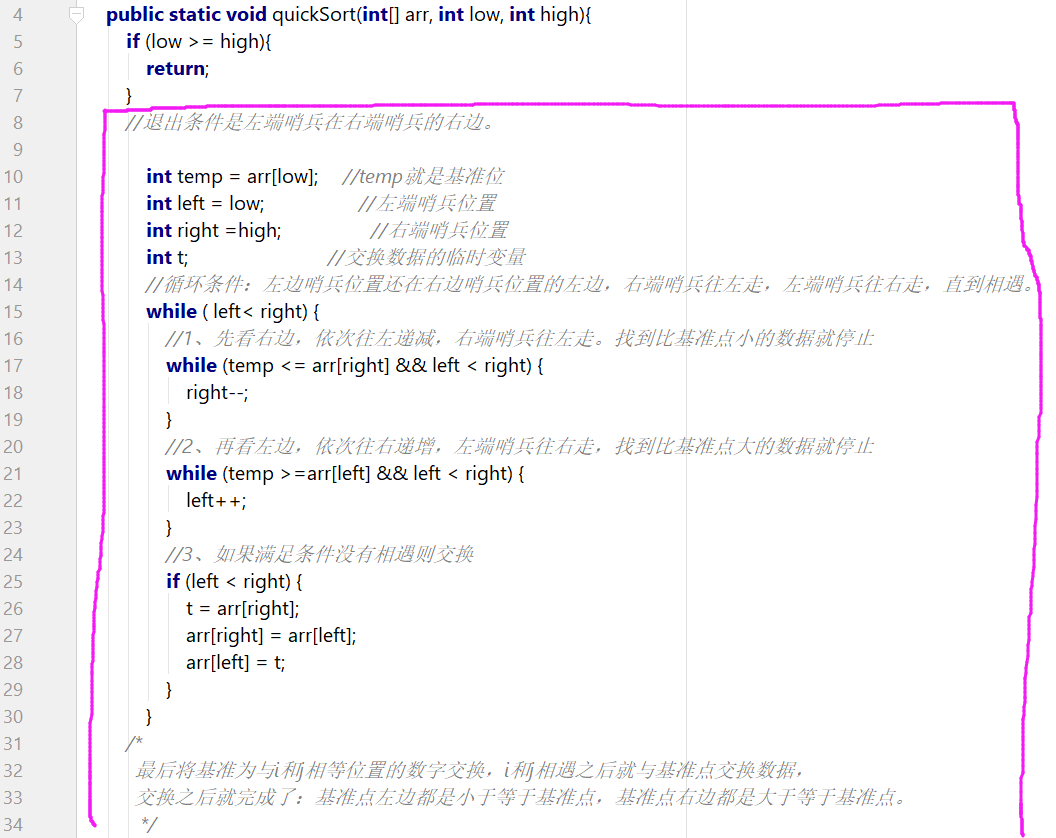
6)快速排序问题。
原表达式:void quickSort(int[] arr, int low, int high)。表达的是对数组arr中的第一位进行定位,让low所在的第一位满足:左边的都小于他,右边的都大于它。low表示数组第一位索引,hight表示数组最后一位索引
等价表达式:先将数组进行分一次分割成两半,使其满足第一个元素归位(该元素最左边小于该元素,该元素最右边大于该元素)+ 该元素左半数组排序 + 该元素右半数组排序。
最小问题规模处理:当只有一个元素,即low >= hight时,就返回结束,本次调用。

总结:递归思想:等价表达式。
原表达式 = 等价表达式 + 临界处理。
二叉树中:
(1)求二叉树第k层的节点数。
原表达式:int layerNodes(SimpleNode<T> root,int k)。Node节点中至少包含T类型的数据元素和左右子节点,该表达式表达的是:求以root为根节点的这颗树第k层的节点个数。
等价表达式:layerNodes(root.left, k - 1) + layerNodes(root.right, k - 1)。因为对root这棵树求第k层的节点数,这个问题可以转化为:分别求出该root树的左右子树的第k-1层的节点数,然后相加就是这棵树第k层的子节点数。
最小问题规模处理:当等价表达式递归到最后的叶子节点时就退出,即当k == 1时,即表示root这棵树的第一层,那就是本身,故子节点树为1,即返回1。
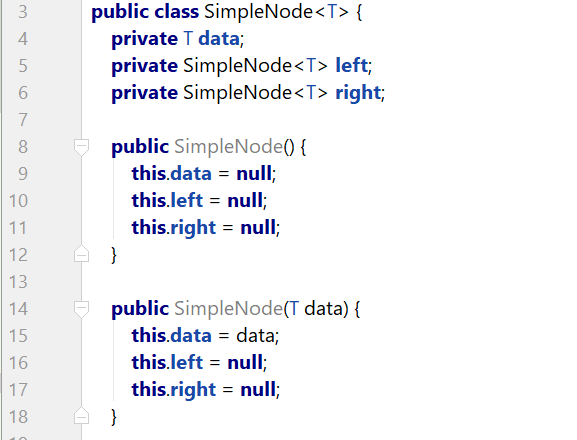
注意:下面是另外一个class文件:这只是截取文件中部分片段。

(2)求二叉树中叶子节点的个数
a、如果二叉树为空,返回0;
b、如果二叉树不为空且左右子树为空,返回1;
c、如果二叉树不为空,且左右子树不同时为空,等价于:返回左子树中叶子节点个数加上右子树中叶子节点个数。
原表达式:int leafs(SimpleNode<T> root)。表示求一棵树的叶子节点数目,这棵树是以root为根节点的树。
等价表达式:root这棵树的左右子树的叶子节点数目之和。
最小问题规模处理:当这棵树递归到没有左右子树时,即一颗只有根节点的数,当然只有一个叶子节点了。
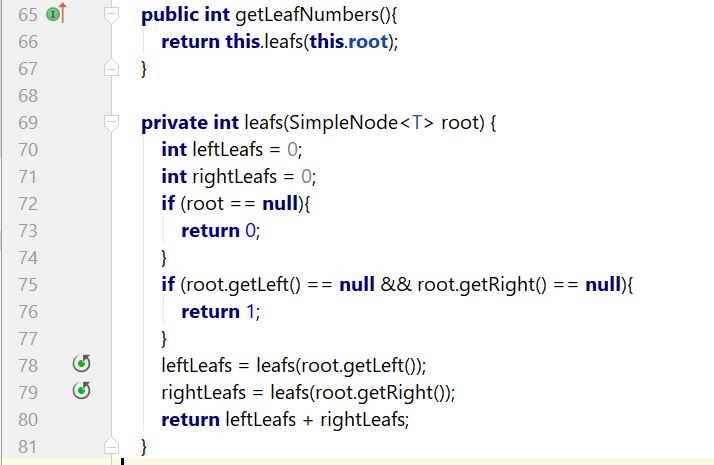
(3)求二叉树中的节点个数。
a、如果二叉树为空,节点个数为0;
b、如果二叉树不为空,二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 1。
原表达式:int nodesTMP(SimpleNode<T> root)。表达的是:求这棵树的节点数,这棵树是以root为根节点的树。
等价表达式:这棵树的左右子树的节点数之和。
最小问题规模处理:这棵树是空树,那么空树的节点数就是0;

(4)求二叉树的深度
a、如果二叉树为空,二叉树的深度为0。
b、如果二叉树不为空,二叉树的深度 = max(左子树深度, 右子树深度) + 1。
原表达式:int heightTMP(SimpleNode<T> root)。表达的是:求这棵树的节点数,这棵树是以root为根节点的树。
等价表达式:这棵树的左右子树的节点数之间的最大值。
最小问题规模处理:这棵树是空树,那么空树的高度就是0;

(5)求二叉树的前序遍历。
a、如果二叉树为空,返回。
b、如果二叉树不为空,先访问根节点,然后前序遍历左子树,再前序遍历右子树。
原表达式:void preOrderTraversalTMP(SimpleNode<T> root)。表达的是:求这棵树的前序遍历,这棵树是以root为根节点的树。
等价表达式:先访问这棵树的根节点,再对左子树进行前序遍历,然后对其右子树进行前序遍历。
最小问题规模处理:如果这棵树是空树,那么就返回;
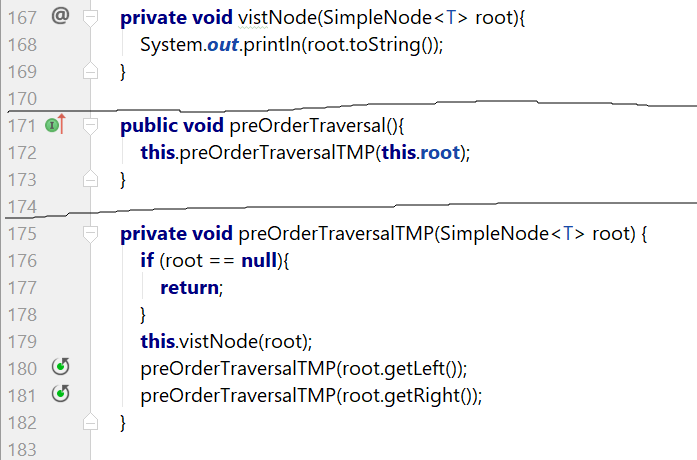
(6)求二叉树的中序遍历。
a、如果二叉树为空,返回。
b、如果二叉树不为空,先中序遍历左子树,然后访问根节点,再中序遍历右子树。
原表达式:void inOrderTraversalTMP(SimpleNode<T> root)。表达的是:求这棵树的前序遍历,这棵树是以root为根节点的树。
等价表达式:先对左子树进行前序遍历,再访问这棵树的根节点,然后对其右子树进行前序遍历。
最小问题规模处理:如果这棵树是空树,那么就返回;
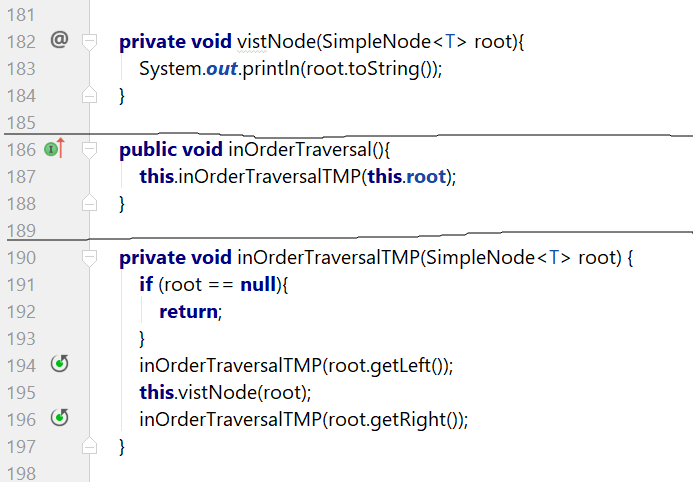
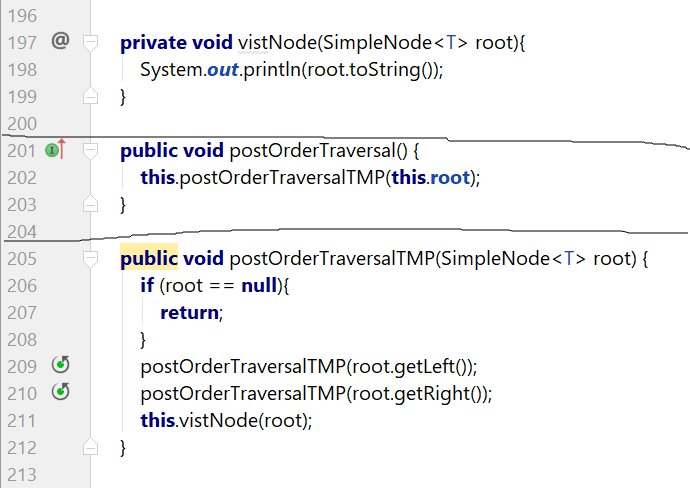
(6)求二叉树的后序遍历。
a、如果二叉树为空,返回。
b、如果二叉树不为空,先后序遍历左子树,然后后序遍历右子树,再访问根节点。
原表达式:void postOrderTraversalTMP(SimpleNode<T> root)。表达的是:求这棵树的前序遍历,这棵树是以root为根节点的树。
等价表达式:先后序遍历左子树,然后后序遍历右子树,再访问根节点。
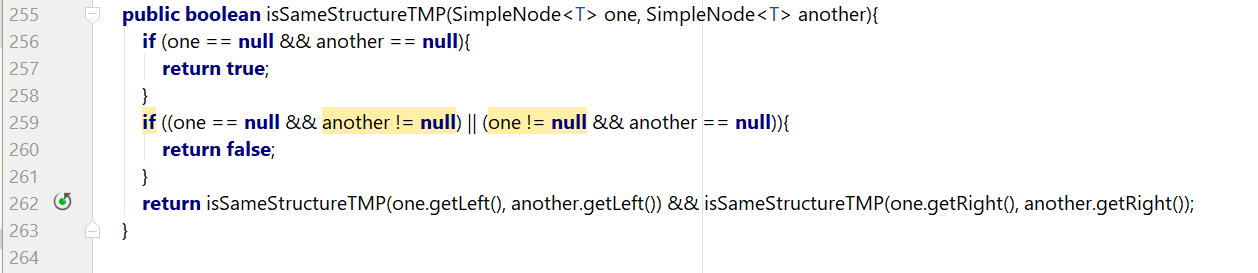
(7)判断两棵二叉树是否结构相同。
不考虑数据内容。结构相同意味着对应的左子树和对应的右子树都结构相同。
a、如果两棵二叉树都为空,返回真;
b、如果两棵二叉树一棵为空,另一棵不为空,返回假;
c、如果两棵二叉树都不为空,如果对应的左子树和右子树都同构返回真,其他返回假 。
原表达式:boolean isSameStructureTMP(SimpleNode<T> one, SimpleNode<T> another)。表达的是:比较两棵树的结构是否相同。
等价表达式:两棵树的左右子树分别对应结构是否相同。
最小问题规模处理:如果两颗棵树都是空树,那么就返回true,如果两棵树只有一棵树为空树,则返回false;
(8)八皇后问题。