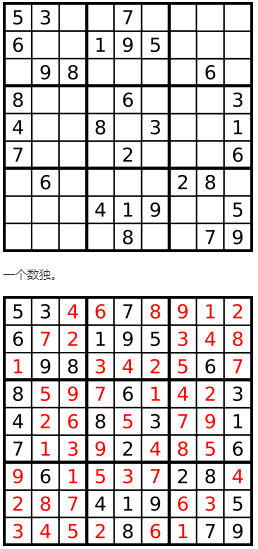
一.解数独
编写一个程序,通过已填充的空格来解决数独问题。
一个数独的解法需遵循如下规则:
- 数字 1-9 在每一行只能出现一次。
- 数字 1-9 在每一列只能出现一次。
- 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 '.' 表示。
class Solution { // box size int n = 3; // row size int N = n * n; int [][] rows = new int[N][N + 1];//记录每行数字d是否存在 int [][] columns = new int[N][N + 1];//记录每列数字d是否存在 int [][] boxes = new int[N][N + 1];//记录每个box是否存在d char[][] board; boolean sudokuSolved = false; public boolean couldPlace(int d, int row, int col) { /* Check if one could place a number d in (row, col) cell */ int idx = (row / n ) * n + col / n; return rows[row][d] + columns[col][d] + boxes[idx][d] == 0; } public void placeNumber(int d, int row, int col) { /* Place a number d in (row, col) cell */ int idx = (row / n ) * n + col / n; rows[row][d]++; columns[col][d]++; boxes[idx][d]++; board[row][col] = (char)(d + '0'); } public void removeNumber(int d, int row, int col) { /* Remove a number which didn't lead to a solution */ int idx = (row / n ) * n + col / n; rows[row][d]--; columns[col][d]--; boxes[idx][d]--; board[row][col] = '.'; } public void placeNextNumbers(int row, int col) { /* Call backtrack function in recursion to continue to place numbers till the moment we have a solution */ // if we're in the last cell // that means we have the solution if ((col == N - 1) && (row == N - 1)) { sudokuSolved = true; } // if not yet else { // if we're in the end of the row // go to the next row if (col == N - 1) backtrack(row + 1, 0); // go to the next column else backtrack(row, col + 1); } } public void backtrack(int row, int col) { /* Backtracking */ // if the cell is empty if (board[row][col] == '.') { // iterate over all numbers from 1 to 9 for (int d = 1; d < 10; d++) { if (couldPlace(d, row, col)) { placeNumber(d, row, col); placeNextNumbers(row, col); // if sudoku is solved, there is no need to backtrack // since the single unique solution is promised if (!sudokuSolved) removeNumber(d, row, col); } } } else placeNextNumbers(row, col); } public void solveSudoku(char[][] board) { this.board = board; // init rows, columns and boxes for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { char num = board[i][j]; if (num != '.') { int d = Character.getNumericValue(num); placeNumber(d, i, j); } } } backtrack(0, 0); } }