部分内容转自:https://www.cnblogs.com/xiaoningmeng/p/5861154.html
因为刚开始学,所以有些可能讲解的不是特别好。
manacher算法(民间称马拉车算法233)是用来找字符串中的最长回文子串的,先来说一下什么是回文串,像这样“abcba”这样一个字符串找到一个中间位置,然后分别向他的左边和右边相等的距离位置的字符是相同的,那么这个字符串就称为回文串,“abcba”这个字符串的len为5是奇数,我们可以找到一个中间字符,然后进行搜索也可以找出来(当然时间复杂度是比较高的),但是当我们遇到一个长度为偶数的字符串时该怎么找中间字符呢,像这样“abccba”,下面我们引入Manacher算法,这是一个可以将长度为奇数或偶数的字符串一起考虑的神奇算法
Manacher算法可以将长度为奇数和偶数的回文串一起考虑:在原字符串的相邻字符串之间插入一个分隔符,字符串的首尾也要分别添加,注意分隔符必须是原字符串中没有出现过的
| 原字符串s | a | b | a | b | c |
| 转换后字符串str | # | a | # | b | # | a | # | b | # | c | # |
一、Len数组的简单介绍
Manacher算法中用到一个非常重要的辅助数组Len[i]表示以str[i]为中心的最长回文子串的最右端到str[i]位置的长度,比如以str[i]为中心的最长回文串是str[l,r],那么Len[i]=r-i+1
| 转换后的字符串str | # | a | # | b | # | a | # | b | # | c | # |
| Len | 1 | 2 | 1 | 4 | 1 | 4 | 1 | 2 | 1 | 2 | 1 |
Len[i]数组有一个性质,Len[i]-1就等于该回文串在原串s中的长度
证明:在转换后的字符串str中,所有的回文串的长度都是奇数,那么对于以str[i]为中心的最长回文串的长度为2*Len[i]-1,其中又有Len[i]个分隔符,所以在原字符串中的长度就是Len[i]-1,那么剩下的工作就是求Len数组
二、Len数组的计算
从左往右开始计算,假设0<=j<=i,那么在计算Len[i]时,Len[j]已经计算过了,设mx为之前计算过的最长回文串的右端点,id为取得这个端点值得位置(那么Len[id]=mx-id+1)
第一种情况:i<=mx.
找到i相对于id的对称位置,设为j,再次分为两种情况:
1、Len[j]<mx-i
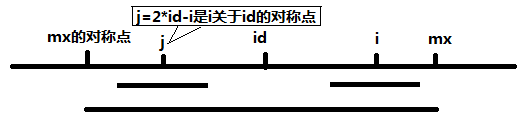
mx的对称点为2*id-mx,i和j所包含的范围是2*Len[j]-1
那么说明以j为中心的回文串一定在以id为中心的回文串内部,且i和j关于id对称,由回文串的定义可知,一个回文串反过来仍是回文串,所以以i为中心的回文串长度至少和以i为中心的回文串长度相等,即Len[i]>=Len[j].因为Len[j]<mx-i所以i+Len[j]<mx,由对称性可知Len[i]=Len[j].
2、Len[j]>=mx-i
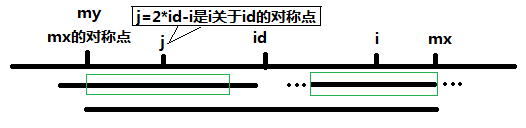
由对称性说明以i为中心的回文串可能延伸到mx之外,而大于mx的部分我们还没有进行匹配,所以要从mx+1位置开始一个一个匹配直到失配,从而更新mx和对应的id以及Len[i]
第二种情况,i>mx
如果i比mx还大,说明对于中点为i的回文串一点都没匹配,这个时候只能一个个匹配(滑稽),匹配完成后更新mx的位置和对应的id及Len[i].
下面推荐一道模板题:luogu P3805 【模板】manacher
#include<bits/stdc++.h> using namespace std; const int N = 11000001; char s[N*2],str[N*2]; int len[N*2],lenn; void getstr() { int k=0; str[k++]='$'; for(int i=0;i<lenn;i++) str[k++]='#',str[k++]=s[i]; str[k++]='#'; lenn=k; } void manacher() { getstr(); int mx=0,id; for(int i=1;i<lenn;i++) { if(mx>i)len[i]=min(len[2*id-i],mx-i); else len[i]=1; while(str[i+len[i]]==str[i-len[i]]) len[i]++; if(len[i]+i>mx) mx=len[i]+i,id=i; } } int main() { cin >> s; lenn=strlen(s); manacher(); int ans=1; for(int i=1;i<lenn;i++) ans=max(ans,len[i]); cout<<ans-1; }