版权声明:
本文由SimonLiang所有,发布于http://www.cnblogs.com/idignew/。如果转载,请注明出处,在未经作者同意下将本文用于商业用途,将追究其法律责任。
感知器
1.问题
人工神经网络(ANN)是机器学习的一重要分支,在没介绍神经网络之前,有必要先介绍感知器,感知器是人工神经网络的前身。
有这么一个问题,我们知道某人的体重及身高可否估计出人体脂肪的含量比例(就是肥瘦问题了)?
而实际的
在这之前,我们随机在街上找了几百人做测量,测量下面的数据:
1。年龄(岁)
2。体重(公斤)
3。身高(厘米)
4。颈围(厘米)
5。胸围(厘米)
6。腹部(厘米)
7。臀围(厘米)
8。大腿围(厘米)
9。膝围(厘米)
10。踝周长(厘米)
11。肱二头肌(扩展)腰围(cm)
12。前臂围(厘米)
13。腕围(厘米)
最后是测量这个人的脂肪比例(百分比)
看看是上面的13个因素和身体的脂肪比例有没关系?
为了方便理解,这里只选取测量的体重(X1)及身高(X2)中30组数据为说明对象,数据如下:
| 编号 | x1 体重(kg) | x2 身高(cm) | y 脂肪含量(%) |
| 1 | 70 | 172 | 12 |
| 2 | 79 | 184 | 6 |
| 3 | 70 | 168 | 25 |
| 4 | 84 | 184 | 10 |
| 5 | 84 | 181 | 29 |
| 6 | 95 | 190 | 21 |
| 7 | 82 | 177 | 19 |
| 8 | 80 | 184 | 12 |
| 9 | 87 | 188 | 4 |
| 10 | 90 | 187 | 12 |
| 11 | 84 | 189 | 7 |
| 12 | 98 | 193 | 8 |
| 13 | 82 | 177 | 21 |
| 14 | 93 | 181 | 21 |
| 15 | 85 | 177 | 22 |
| 16 | 74 | 168 | 21 |
| 17 | 89 | 180 | 29 |
| 18 | 95 | 180 | 23 |
| 19 | 83 | 172 | 16 |
| 20 | 96 | 187 | 17 |
| 21 | 81 | 173 | 19 |
| 22 | 91 | 177 | 15 |
| 23 | 64 | 173 | 16 |
| 24 | 67 | 178 | 18 |
| 25 | 69 | 172 | 14 |
| 26 | 72 | 182 | 4 |
| 27 | 60 | 171 | 8 |
| 28 | 67 | 171 | 23 |
| 29 | 60 | 164 | 4 |
| 30 | 73 | 175 | 9 |
-----
2.思路
思路是这样的,能否找到w1,w2,w0,使得y~=w1*x1+w2*x2+w0*x0(其中定义xo=1),这样只要求出w1,w2,wo就可以解决一开始的问题。
于是,我们把上面的模型简化为:

然后让h尽可能接近y的。
---
3.模型
于是每一组数据(一行为一组数据)输入到模型中有了(例子中共30组数据):

上面的其中一组数据可以简化写成:

定义一个函数J,通过函数J来衡量w1,w2,w0是否合适:
J=1/2*(([h(1)-y(1)])2+([h(2)-y(2)])2+...([h(30)-y(30)]) 2)
简写成:

-----
4.求导
下面的工作就是如何求w1,w2,w0了,
由于上面的式子中未知的只有w1,w2,w0(每一组的x1,x2,y都是知道的),
那么函数J实际上就是关于变量(w1,w2,w0)的函数。
为了方便理解,我们暂时把w0=0,这样
J=f(w1,w2)了
对应一个二元方程来说,可以通过一个立体图来直观的描述:

现在就是如何求出最低的位置。
这里用到的是一种称为梯度下降的方法,
首先,随意给定一个点A,然后求出其所在位置的最陡峭的方向(用偏导的方式),再给定一定长度,往下走一点,
停下来再求最陡峭的方向,然后往下走一点,循环直到到达最低的位置。
如下图,

上面的是一个比较好理解的情形,实际上这个J(w1,w2,w0)是一个难以用图表示的,但道理是一样的。
下面给出w1求偏导的具体过程,真的的很详细。。。(可怜的电脑编辑公式实在慢)。

同理求出w2,及w0的偏导(注意x0=1);
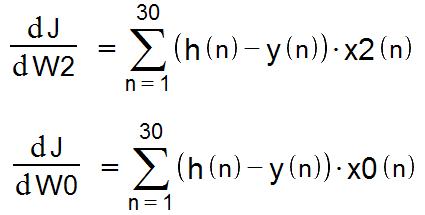
---
5.梯度下降求答案
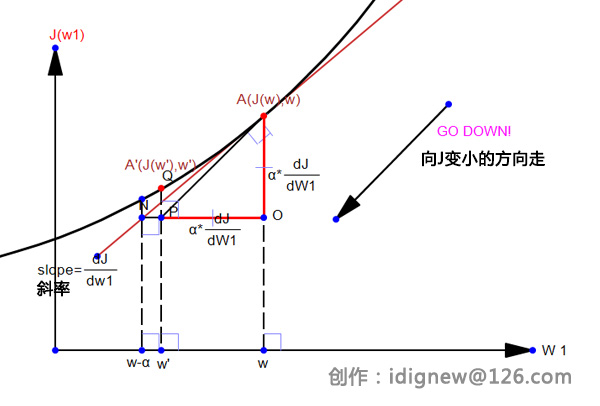
求出偏导后,可以设定一个固定的步长α,向低洼的地方出发了。
下面的公式中的“:=”为编程中的更新公式

代入上面的求导结果后

为了形象的说明为什么减去“α*偏导”,下图形象的说明,其中w’为更新后的w值
---
6.代码实现
%数据
bodyData =
1 70 172 12
1 79 184 6
1 70 168 25
1 84 184 10
1 84 181 29
1 95 190 21
1 82 177 19
1 80 184 12
1 87 188 4
1 90 187 12
1 84 189 7
1 98 193 8
1 82 177 21
1 93 181 21
1 85 177 22
1 74 168 21
1 89 180 29
1 95 180 23
1 83 172 16
1 96 187 17
1 81 173 19
1 91 177 15
1 64 173 16
1 67 178 18
1 69 172 14
1 72 182 4
1 60 171 8
1 67 171 23
1 60 164 4
1 73 175 9
%% matlab 代码
%加载数据 x=bodyData(:,1:3);%注意x(:,1)=1; y=bodyData(:,4); %初始化 step=0.000001;%设定步长,就是 stepn=1;%步骤数 w=[-0.5;0.5;-0.5];%初始化w值,注意w(1)对应的是上面的x0; while stepn<500; h=x*w; %计算出h e=(h-y); %计算出差值e e1=e.*x(:,1); e2=e.*x(:,2); e3=e.*x(:,3); w(1)=w(1)-step*sum(e1);%计算出w1,就是上面讲的w0; w(2)=w(2)-step*sum(e2);%计算出w1,就是上面讲的w1; w(3)=w(3)-step*sum(e3);%计算出w1,就是上面讲的w2; J(stepn)=1/2*sum(power(e,2)); %计算出代价函数J; if stepn>1 J_gradient=J(stepn-1)-J(stepn); %计算梯度值 end %绘制图形 plot(stepn,J(stepn),'o'); hold on; title(['步数=',num2str(stepn),' 梯度=',num2str(J_gradient)]); pause(0.1); %暂停0.5秒 stepn=stepn+1; end
运行结果:
最后的w值:
w =
-0.4979
0.6018
-0.1820
----
7 后话
1.关于数据扩充
对于上面的例子,可以很容易把上面的3个x变为m个x,数据从30个变为m个。

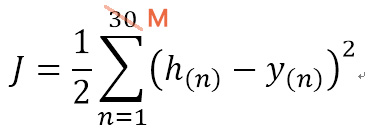
2.关于BGD与SGD,还有Mini-BGD。
还记得上面的

留意一下,这个是需要对整个数据集都要求和计算的。
而对整体求出梯度的下降方式是叫批量梯度下降(Batch Gradient Descent,简称BGD);
如果数据的维度少(所谓维度就是x1,x2,x3,...,xn,如果上面的例子就是体重,身高,腰围等)的数据没问题。
但对于大数据,如图形那样过万的维度数据,效率就很低了。
所以就有了随机梯度下降,Stochastic Gradient Descent(简称SGD),
及常用的小批量梯度下降 Mini Batch Gradient Descent。
这里不展开,有兴趣可以Search一下区别。
3.关于编程
对应上面的数据,或者类似这样的数据,要做线性回归,
可以自己不写代码,而matlab有一个简单的方式可以实现:
% 把上面的数据用regress 函数就可以解决
w = regress(y,x)
ans:
w =
116.0441
0.5502
-0.8103
参考:
NG大牛的
好了,就写到这里。
(end)