用SV写一个蒙哥马利模乘的参考模型

前言

往期推送过一个蒙哥马利算法的介绍，如果要实现蒙哥马利模乘的硬件模块，那么一个参考模型是必不可少的，这一期将利用SV实现一个简单的参考模型，这个参考模型可以直接用于功能仿真

根据以往推送中的运算流程进行建模

类的定义

  class BN;
    rand bit [127:0] num [32:0];
    string name;

    constraint c {num[32]==0;num[0][0]==1;};

    function new(string name="A");
      this.name = name;
    endfunction
      
  endclass : BN

定义一个大数的类，计算的位宽是4096，而使用的基是128bit也就是基为(2^{128})，数组大小定义为33，用于处理数运算时的溢出。

大数显示

    // BN display
    function void BN_display(bit flag=0);
        string s;
        s={s,name,":"};
        if(flag==1)
        s={s,$sformatf("%h",num[32])};
        for (int i=1; i<32+1; i++) begin
        s={s,$sformatf("%h",num[32-i])};
        end
        s={s,"
"};
        $display(s);
    endfunction : BN_display

默认不打印num[32]

大数移位

// BN_shift
function void BN_shift();
    for (int i=0; i<32; i++) begin
    num[i] = num[i+1];
    end
    num[32] = 0;
endfunction : BN_shift

蒙哥马利算法中有/b的操作，我们选取(2^{128})为基，那么这个操作就能使用移位实现，运算的大数为无符号数，最高为补0

大数乘法

    // BN_mul
    function void BN_mul(bit [127:0] a,BN ans);
        bit [255:0] temp;
        bit [127:0] carry;
      for (int i = 0; i < 32; i++)
      begin
          temp = num[i] * a + carry;
          ans.num[i] = temp[127:0];
          carry = temp>>128;
      end
      ans.num[32] = carry;
    endfunction : BN_mul

实现的是4096*128位的乘法，用于计算(y_i cdot x)和(u cdot N)

大数加法

  // BN_add
  function automatic void BN_add(input BN a,b,ref BN c);
    bit [128:0] psum;
    bit carry;
    carry =0;
        for (int i = 0; i < 32+1; i++)
        begin
            psum = a.num[i] + b.num[i]+ carry;
            c.num[i] = psum;
            carry = psum[128];
        end
  endfunction : BN_add

计算两个大数的加法

大数减法

利用取补码，然后相加实现

取补码

取反加一

    // BN_com
    function void BN_com(ref BN c);
        BN temp,b;
        temp = new("temp");
        b = new("b");
        for (int i=0; i<32+1; i++) begin
                temp.num[i]=~this.num[i];
                b.num[i]=0;
        end
        b.num[0]=1;
        BN_add(temp,b,c);
    endfunction : BN_com

实现减法

  // BN_sub
  function automatic void BN_sub(input BN a,b,ref BN c);
        BN com;
        com =new("com");
        b.BN_com(com);
        BN_add(a,com,c);
  endfunction : BN_sub

计算(omega)

计算原理如下图，下图有一处错误，循环变量中的(omega)和我们所求的(omega)并不是一个变量，这里指的是我们基的bit数

//              BN_w
    function void BN_w(output bit [127:0] w);
        bit[127:0] t;
        bit[255:0] tt;
        t=1;
        tt=0;
        for (int i=0; i<127; i++) begin
                tt=t*t;
                t=tt[127:0];
                tt=t*num[0];
                t=tt[127:0];
                $display("%h",t);
        end
        tt=0-t;
        w=tt[127:0];
    endfunction

大数比较

最后输出时要检查r是否小于N

//              BN_cmp return 1 when this >= a
    function bit BN_cmp(input BN a);
        for (int i=0; i<32+1; i++) begin
                if(num[32-i]<a.num[32-i])
                        return 0;
                if(num[32-i]>a.num[32-i])
                        return 1;
        end
        return 1;
    endfunction

蒙哥马利模乘

有了上面的函数，我们就能实现蒙哥马利模乘啦

  // BN_sub
  function automatic void mont_mul(input BN x,y,N,ref BN r);
        BN temp1,temp2,temp3;
        bit [127:0] u,w;
        bit [255:0] ut;
        temp1=new("temp1");
        temp2=new("temp2");
        temp3=new("temp3");
        N.BN_w(w);
        $display("%h",w);
        x.BN_display();
        y.BN_display();
        N.BN_display();
        r.BN_display();
        for (int i=0; i<32; i++) begin
                ut=y.num[i]*x.num[0];
                u=ut[127:0];
                ut=r.num[0]+u;
                u=ut[127:0];
                ut=u*w;
                u=ut[127:0];
                x.BN_mul(y.num[i], temp1);
                N.BN_mul(u, temp2);
                BN_add(r, temp1, temp3);
                BN_add(temp3, temp2, r);
                r.BN_shift();
        end
        if(r.BN_cmp(N)) begin
                BN_sub(r,N,temp1);
                r.num=temp1.num;
        end
        $display("x*y*p^-1 mod N:");
        r.BN_display();
  endfunction : mont_mul

tb测试

顶层文件内容为

module tb;
        import BN_pkg::*;

        initial begin
                BN x,y,N,r;
                x=new("x");
                y=new("y");
                N=new("N");
                r=new("r");
                void'(x.randomize());
                void'(y.randomize());
                void'(N.randomize());
                mont_mul(x,y,N,r);
        end

endmodule

我们运行一次

那么如何验证是否正确呢，我们使用python检查一下，python自带了大数运算的库，可以自动的计算大数模乘。

下面的python代码用也模拟了一遍蒙哥马利模乘的流程，与直接模乘进行对比。蒙哥马利模乘的计算结果实际上是(x cdot y cdot ho^{-1} mod N)，所以要将结果再乘以一个( ho)才能进行对比。把上述打印出来的结果复制到python中运行，进行检查。

# tranfer long num to array
def tranBN(bn,bn_a):
  bn_t=bn
  for x in range(0,32):
    bn_a[x] = bn_t % 0x100000000000000000000000000000000
    bn_t = bn_t >> 128

# -n^(-1) mod 2^128
def get_w(n):
  nw=n % 0x100000000000000000000000000000000
  w=1;
  for x in range(0,127):
    w=w*w % 0x100000000000000000000000000000000
    w=w*nw % 0x100000000000000000000000000000000
    # print("w:%x" %w)
  w=0x100000000000000000000000000000000-w
  return w

# p mod n
def get_p():
  t=1
  for x in range(0,4096):
    t=(t<<1)
    t=t%c
  return t


if __name__ == '__main__':
  a = 0xdaaf6a1e33805c0f68e58a95cc39b4c64594dbc4f2b0ba88aae650f51e467e1c4f10ba102d77eb77c1547e0c40e6d7aeb05539c308ea01dafb6da336492100ab2cdd38a580091aaec64d74192431c00cce4f4c752498e88aaa5ccc010b2317db8e01c0660e1dc9ba01154024448965f8209721d39158422ef2e1817ac4240be53bfc0f05b7336e172e271c9e9fcd38057746bbe8f5bb1907ab681ae012395e78e531f5291340108b4f8b182614a29fa0c7a44032229fe3fb3af01a5577cf335f318c1ecc70b613e7532ab85dc087c618020e949640cb14a3dbf634fa0b48f0098c9e9ee4861a5e6193f2a9241e28d1f4d3c9a8f11c460943dbd7b7b06f18fe75454e20593388dcaa8b98aabe293987d22e2725251d6ebf2729cde05db076ed775b7f369d1f9e1109812960b8b76e333bcca8aaa98931c2937cadb68a4ffc6c54eff9a6bcb77da76dc02fcb83167105319dd5a25f19d6ef0b214927120635e665afe46f681259247978d4a6853bb3cac03bc554d07003496f6b8b624bfec45f4cfb24acded0aeb074e8f70df1813ebb26bd5fe26be2a627684d793a8a052e3a9476a1d9697dd9e27beb4db7ad01eb8b0a3b5c7717d716ebd30727cc7786a17f09b04d6b94a56d9f70ac514e026f42834486e6a0852cef4808c7222cc02e908f2ab225f93e316612d1fd67359987ab7a23be6348b73f6764e60de2edf72c500ebf
  b = 0x14b8f4973aacf4927678c823e8c5988fe76caf5b4241b1a32954ccb35729ff3573f617bc077c8d165ec5270c0b863fc231ae96dd5d933e9a98abdaf3d6e852e98149945ab1a9a90e38e07c3017c1273b18598d87b59a289de9d7c5bc5c6f64cccdbcbec42c289c8b1b799f8454cba6b89e5976a84c19217d64ddde5af42e37ab465928d068deaa3a0270b8d062dbe0b737667c3afd065871532081e72bc1f79e1d7ebd1fb933ec3555a8e986f949f72ca11bc2fbe4c704b20838c68b707d9f3db1d8ae45b44b6bd36a58bfbf7d565347a6c6e20130c84f1bad77f6251e81dfb6ffa9a508d64db7d2fe48b5e4ebe68e7c8d62cdf5ab1c2ca8c2d2e835a1423acbef65956c980dfb62b3a405b9efbc93283d5071c2129b831481c537cc5be8f1d2723f1168f797bde736c1f73054d7d0dc97538fba25bb3e38703934d8fc46ad22eb23ea409184c3dba8241efc92ce5a6728f4385da637bc23ef7acb506d0543804ae7d660926a82406f9d3206376d5454466ecde2246a125c99aebdf16743d55cfb1c4ab0fdb8387320d541a94e3c5aa6038466eaa18682a163d571db3214de448b3d4d7a632bc60f0a524a041cd6e72a75dbc9f6bb63743df3c3c0d4649a28bd0bbeee569182303a66b830a2273b8df05c712adadf2bcb75244a66826265da778e0c3b45a20d6c962fd203e708ff62dd29b9edd96f2afd2bfe92014968e439ef
  c = 0xa35f4906ed176bc241535c78955d02f4d0ac5376d736ae280077887200c758b7781b4432fa8baca2a81ad6fb0817051a00fccf8e15c63048681bcf8342b56433abd550affa489b289cd4f0482adce321c8cf4374ce15267692dfc8b0da108f4bb0e922d4a28402ef785c2516f6296486f8505ac3df05c0f953acce65e2dc5f1e59965ded73fa18ffb482ad1a2e5433d4df8211de12a3e7a71a1a084fed671fb11eeaf76f640c4fd549ea307b6622f798f027786e79232206de1507281d84c719209d408bc85f9ed2e1b82ecf72ff805a45221dc712c45a8dbc375e9b64227ec6b659a75fc5b5e051e776bcd9f4f6d82ebaff89a48c8494d6ed072372b846156af229994baab390ec57c00130255acc2cdf975783df4678153f0ca51b854425b1568b5b8b53239f50dd39fc53c3d41827a0687c435f6de5e98843def3fb7b0f7e701cdfb51517d6628392bd9291c16282556f5581766dd6a0a426a35312237399f93ad69502592c0f6d1864ba0b75600ee04cb406bcb833bc98527a0ac1249c6a918456b06f24611770c1708426b4d9041f7fe83be68fbc7018e461951d234ebf00227b4301911e24055c745203c888276f4db0c05f66514ae4e6b4bf4c8914e36c4a94bf57bf807dd40c7572d1a99c27d9f58af0877bb217c081d750d5edbe3c45eafc3ea6786560fa819873452cc8bffc7ab998ab70496b77fdadffb7e7262d
  t = 1

  a_a=[0 for i in range(32)]
  b_a=[0 for i in range(32)]
  c_a=[0 for i in range(32)]

  tranBN(a,a_a)
  tranBN(b,b_a)
  tranBN(c,c_a)

  w=get_w(c)

  r = 0
# mont mul , get a*b*p^-1 mod c
  for x in range(0,32):
    r0 = r%0x100000000000000000000000000000000
    u = (r0+b_a[x]*a_a[0])*w
    u = u % 0x100000000000000000000000000000000
    r = r+b_a[x]*a+u*c
    # check r[127:0] == 0
    if r%0x100000000000000000000000000000000 == 0:
      pass
    else:
      print("r[127:0]!=0!!!!")
      print(r%0x100000000000000000000000000000000)
    r = r >> 128
    # print("%x"%r)
  if r>c:
    r=r-c
  print("a*b*p^-1 mod c:")
  print("%x"%r)

  t=get_p()

# compare to python

  r_s=(a*b) % c
  r_m=(r*t) % c

  print("python result: 
%x" %r_s)
  print("mntmul result: 
%x" %r_m)
  if r_s==r_m:
    print("result match!")
  else:
    print("result dismatch!")

python中模拟蒙哥马利的结果与sv中一致

而python中模拟蒙哥马利和直接模乘结果也一致

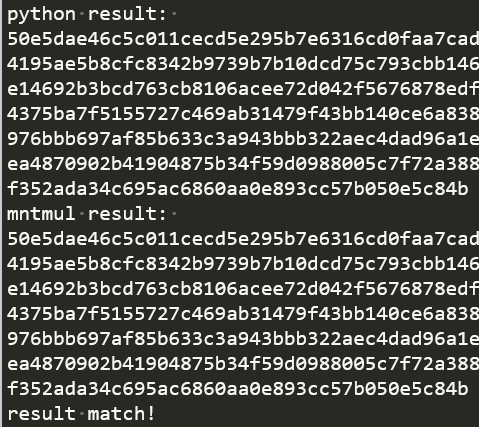
注：结果太长，只截了一部分