欢迎关注个人公众号摸鱼范式

加法器相关
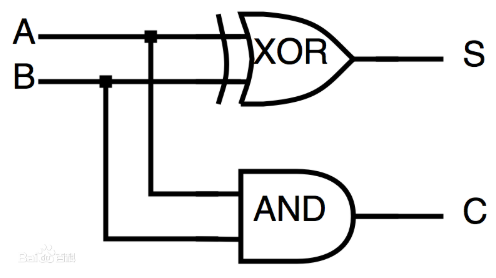
半加器和全加器的区别在于,是否有进位输入端,可以直观地理解为,半加器是两个一比特相加,而全加器是三个一比特相加,输出结果和进位信号。
半加器
半加器的真值表如下图
| 输入 | 输出 | ||
|---|---|---|---|
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
其逻辑表达式为
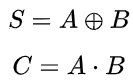
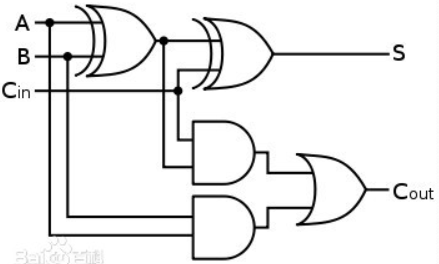
根据逻辑表达式,可以使用如下门电路实现
全加器
全加器真值表如下
| 输入 | 输出 | |||
|---|---|---|---|---|
| A | B | Ci | C | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
其逻辑表达式为:
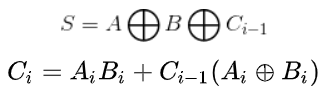
使用门电路搭建
使用加法器计算7bit中1的数量,最少用几个?
有7个1bit的数,为他们编号,从b0到b6,一共七个。
使用1bit全加器可以将3个bit相加,得到2bit的结果,那么b0,b1,b2使用一个加法器,b3,b4,b5使用一个加法器。
现在7个1bit变成了2个2bit和一个1bit(b6)。
然后使用一个2bit全加器将两个2bit数进行相加,1bit的b6作为进位输入。相加后结果为3位,最大可以表示到7个1bit。
而2bit全加器可以有2个1bit全加器组成,所以一共使用4个1bit全加器可以完成1的数量的统计。
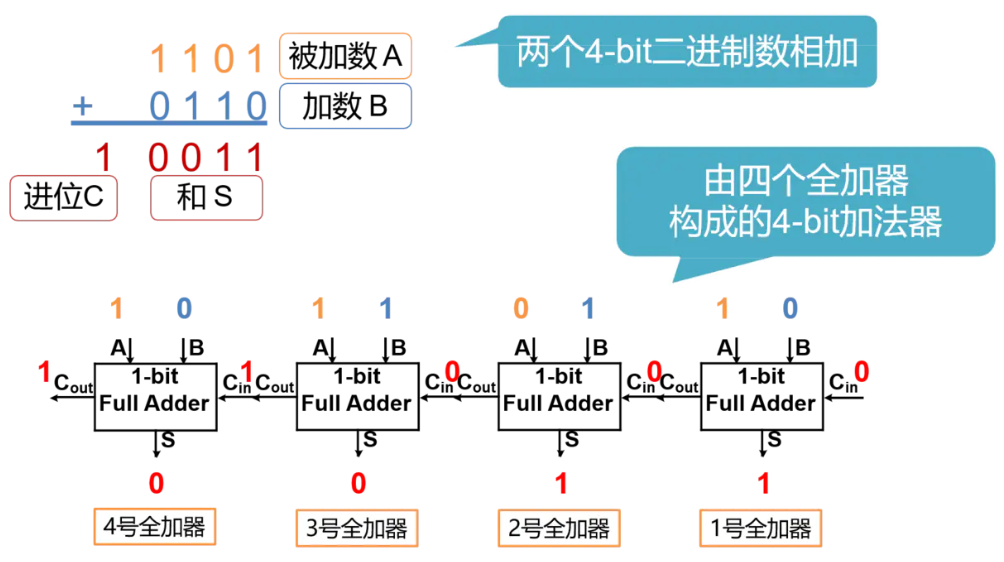
行波进位加法器
以4bit的行波进位加法器为例,需要使用4个1bit加法器实现,如下图所示。在进行加法运算时,首先准备好的是1号全加器的3个input。而2、3、4号全加器的Cin全部来自前一个全加器的Cout,只有等到1号全加器运算完毕,2、3、4号全加器才能依次进行进位运算,最终得到结果。 这样进位输出,像波浪一样,依次从低位到高位传递, 最终产生结果的加法器,也因此得名为行波进位加法器(Ripple-Carry Adder,RCA)。
如果将全加器内部打开,我们可以看到,关键路上有9个门,门延迟非常高
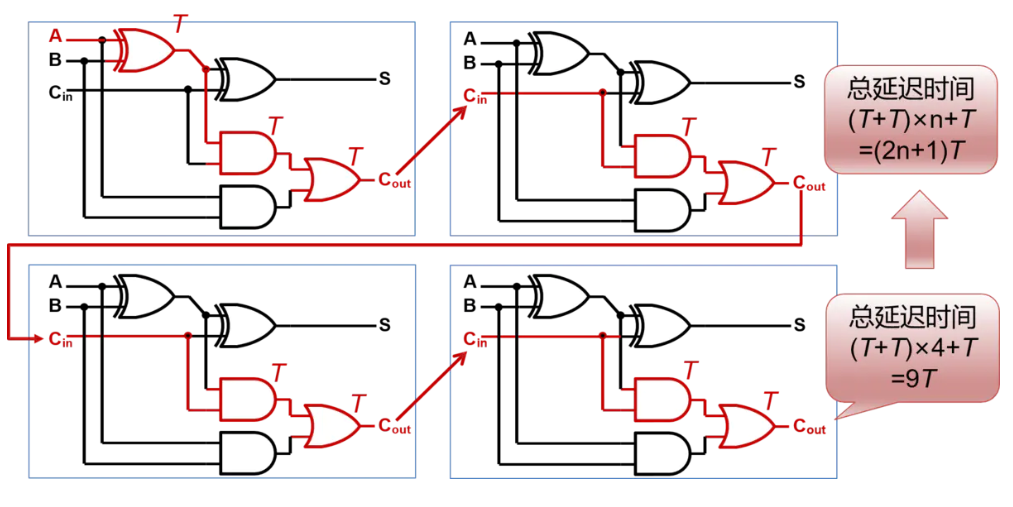
超前进位加法器
为了改进行波仅为加法器的延迟问题,可以将全加器的进位信号转化为有G和P以及本级进位输入组成的逻辑。如下图

将四个加法器串联,迭代可以得到
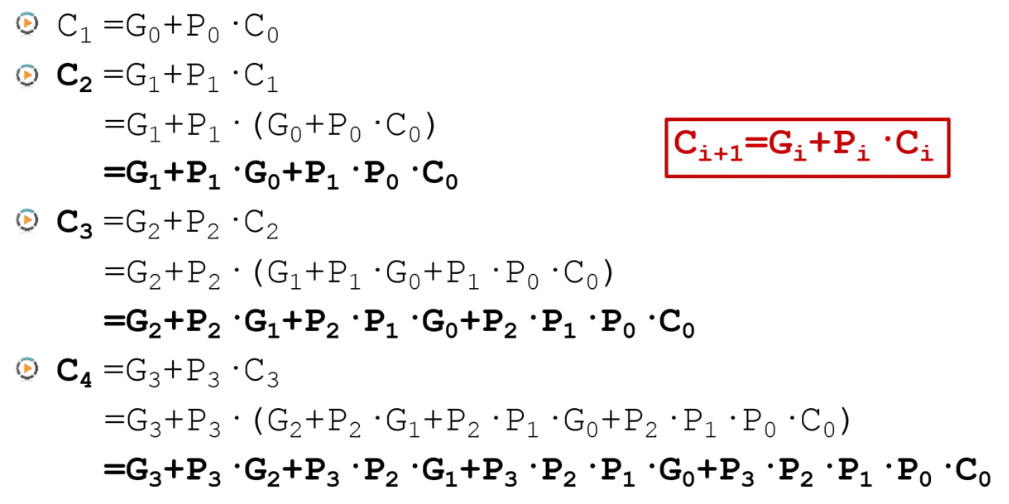
可以看到,每一级的进位都不依赖于上一级的进位,因此不需要等待上一个加法器完成计算,超前得到进位结果。同时,显然如果要实现大位宽加法器,逻辑将会变得更加复杂。
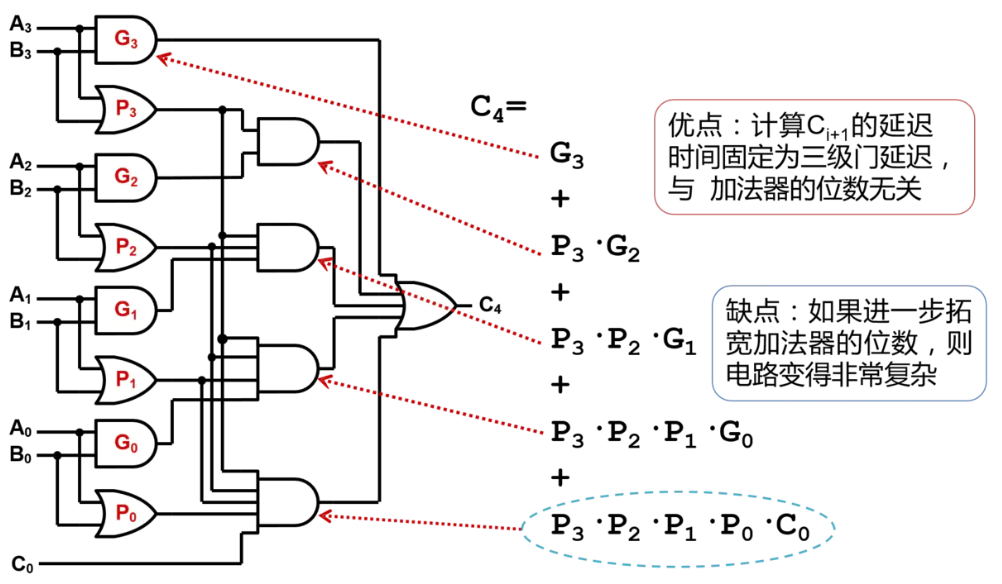
通过超前进位的方法,实现四位全加器的原理图如下
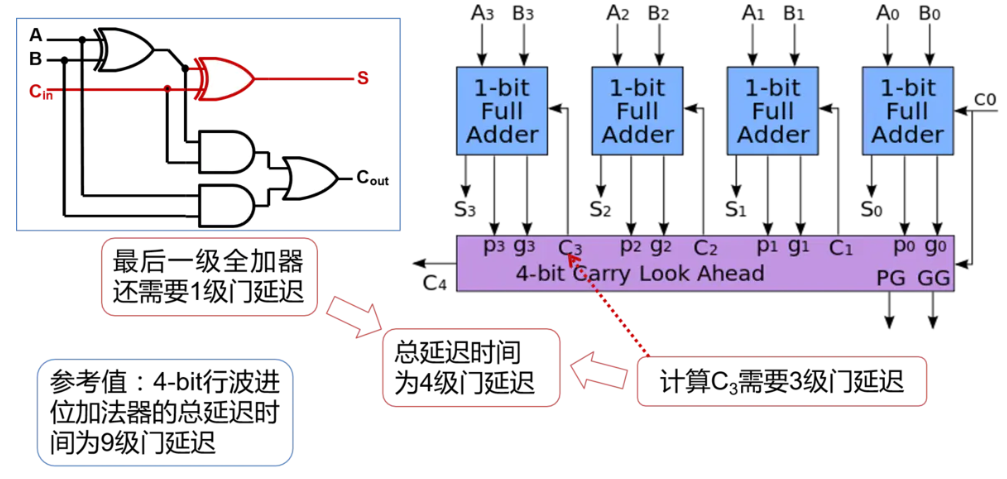
单bit全加器的输出改为输出P、G和S,而每一级的进位可以有下方的逻辑得到。因此最终延迟位4个门。
对比行波进位加法器(RCA)和超前进位加法器(CLA)
| - | RCA | CLA |
|---|---|---|
| 结构特点 | 低位全加器的Cout连接到高一位全加器Cin | 每个全加器的进位输入并不来自于前一级的全加器,而是来自超前进位的逻辑 |
| 优点 | 电路布局简单,设计方便 | 计算Ci+1的延迟时间固定为三级门延迟,与加法器的位数无关 |
| 缺点 | 高位的运算必须等待低位的运算完成,延迟时间长 | 如果进一步拓宽加法器的位数,则电路变得非常复杂 |
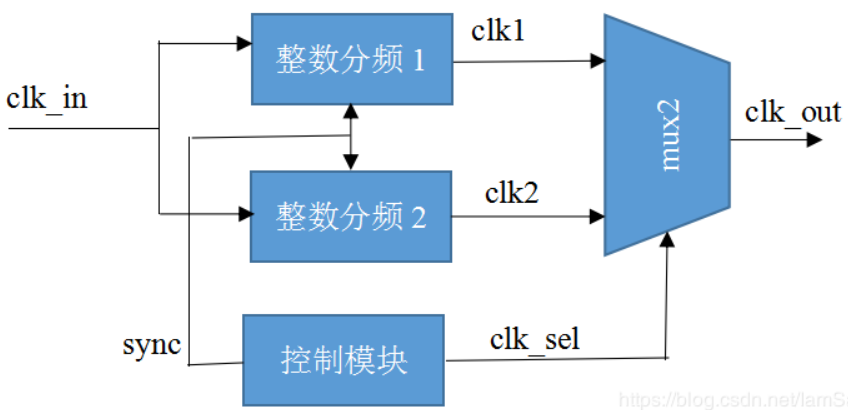
分频电路相关
偶数分频
偶数分频器的实现简单,用计数器在上升沿或者下降沿计数,当计数器的值等于分频系数的一半或等于分频系数时,信号翻转。偶数分频器分频原理如下图所示:
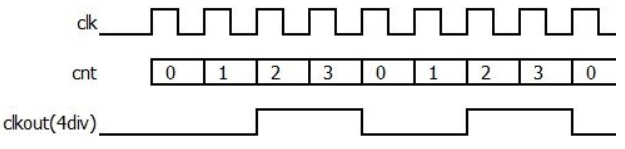
上图的的分频系数是4,就是4分频。电路原理是用一个上升沿计数的计数器,每次计数到2时输出信号clkout翻转一次,每次计数到4时clkout再翻转一次,一直周期重复下去。其他的偶数分频器原理也是一样。
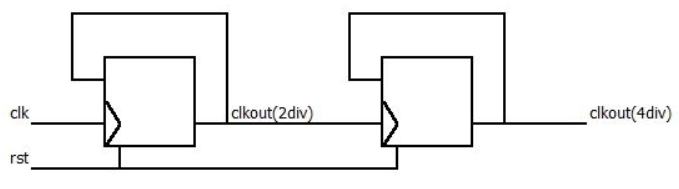
如果偶数分频系数是2的幂,就可以用2分频器级联得到;例如4分频就是两个2分频级联,下图就是用两个2分频器级联得到4分频器。
奇数分频
如果不要求占空比为50%的话,也比较容易实现,如进行三分频,通过待分频时钟上升沿触发计数器进行模三计数,当计数器计数到邻近值进行两次翻转,比如可以在计数器计数到1时,输出时钟进行翻转,计数到2时再次进行翻转。即在计数值在邻近的1和2进行了两次翻转。这样实现的三分频占空比为1/3或者2/3。
对于实现占空比为50%的N倍奇数分频,可以分解为两个通道:
- 上升沿触发进行模N计数,计数选定到某一个值进行输出时钟翻转,然后经过(N-1)/2再次进行翻转得到一个占空比为非50%奇数N分频时钟;
- 下降沿触发进行模N计数,到和上升沿触发输出时钟翻转选定值相同值时,进行输出时钟时钟翻转,同样经过(N-1)/2时,输出时钟再次翻转生成占空比非50%的奇数N分频时钟。
将这两个占空比非50%的N分频时钟或运算,得到占空比为50%的奇数n分频时钟。
具体例子:5分频等占空比,可以通过待分频时钟下降沿和上升沿触发0~4计数,
- 对于待分频时钟的上升沿,当计数器cnt1计数到1时,clk_p翻转;当计数器计数到3(1 + (5 - 1) / 2 = 3)时,clk_p再次反转;
- 对于待分频时钟的下降沿,当计数器cnt2计数到1时,clk_n翻转;当计数器计数到3(1 + (5 - 1) / 2 = 3)时,clk_n再次反转;
- 然后下降沿产生的5分频时钟和上升沿产生的5分频时钟进行或运算,即可得到占空比为50%的N分频时钟。
这种方法可以实现任意的奇数分频。
下面给出5分频的具体代码:
`timescale 1ns/1ps
module CLK_DIV5(
input clk_i,
input rst_n,
output clk_o
);
reg [2:0] cnt1,cnt2;
reg clk_p,clk_n;
//*********************
//MAIN CORE
//*********************
always @(posedge clk_i,negedge rst_n)
if(!rst_n) begin
cnt1 <= 3'b0;
clk_p <= 1'b0;
end
else begin
if(cnt1 == 3'b100) begin
cnt1 <= 3'b0;
clk_p <= clk_p;
end
else begin
cnt1 <= cnt1 + 1'b1;
if(cnt1 == 3'b1 || cnt1 == 3'b11)
clk_p <= ~clk_p;
end
end
always @(negedge clk_i,negedge rst_n)
if(!rst_n) begin
cnt2 <= 3'b0;
clk_n <= 1'b0;
end
else begin
if(cnt2 == 3'b100) begin
cnt2 <= 3'b0;
clk_n <= clk_n;
end
else begin
cnt2 <= cnt2 + 1'b1;
if(cnt2 == 3'b1 || cnt2 == 3'b11)
clk_n <= ~clk_n;
end
end
assign clk_o = clk_p | clk_n;
endmodule
分数分频
对于要求相位以及占空比严格的分数分频(小数分频),建议采用模拟电路实现。而使用数字电路实现只能保证尽量均匀,在长时间内进行分频。
对于一个分数,把他它分为整数部分和小数部分的形式。例如N=M.D>1分频,分为整数M和小数D,我们使用M分频和M+1分频来构成M.D分频。
设M分频的次数为N1,M+1分频的次数为N2。
将M分频进行N1次和M+1分频进行N2次,那么在M*N1+(M+1)*N2个周期内,整体可以看作(M*N1+(M+1)*N2)/(N1+N2)=N分频。
可以通过均匀分布M分频和M+1分频,使得相位较为均匀。
结构图可以参考下图