最近需要做一个空间工字形截面点排序的算法，记下这段过程。
之前做过空间共面四个点的凸包排序，简单的利用旋转即可解决，然而工字形并非凸包，旋转已经无法解决。这里分析其特征，采用多种方法结合来处理。
代码实现时出现求平行点出错，原因是三维坐标中必须写满三个等式才能判断平行，否则遇到沿坐标轴方向极限情形时，判断就会失败。其它更多问题花在了算法优法（如第一点最开始用求中心点，再求最远点的方式找顶点等）、调试笔误上哈哈 (-_-‘)。
步骤职下：
一、如果工字形左侧和右侧的上下端是对齐的。
1、对工字形12个顶点进行代数排序，如此，首尾必是空间上相距最远的两点，这两点是工字形最外围四点中的两个对角pl1、pr4。
2、利用垂直关系找出另外两点pl4、pr1。
3、对四点进行代数排序，取前两点，则该两点要么是左右侧线<pl1,pl4>，要么是上下端线<pl1,pr1>。尝试找共线的点，如果找到两个点pl2、pl3，则为侧线，否则为端线，对找中间两点即得到侧线。
4、利用平行关系，找出与该侧线方向平行的如下点集：左侧和右侧的四个点组合（pl1、pl2、pl3、pl4）、（pr1、pr2、pr3、pr4），中间两组两点组合（plc1、plc2）、（prc1、prc2）。注意算法的精确性，避免极限情形失效。
5、如果对找到的4组点集进行代数排序，所得即为有序的4组点。其中第一点与四个顶点的第一点相同的，认为是特定侧的起点，对中间两组的第一点取出，进行排序，该序列即为中间两组的特定顺序。
6、最后得到4224的点集，且有序。对应关系如下，此时按顺序取出对应点即可：
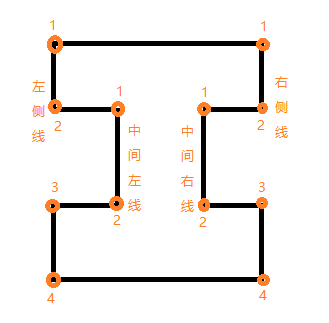
二、如果工字形两侧不确定是否平行，不确定左右或者上下是否对称。
1、对12个点进行代数排序，首尾两点是工字形中最远的两点，但可能是上或者下端部矩形的两个对角（p1、p2）。
2、利用垂直关系，找其它任意两点能以上述一点作为垂足的一组点（p1，p11，p12）。
3、以其中任一方向（p1，p11）对12个点进行平行方向上共线分组排序，得到四组点集2442（从上至下）、或者4224（从左至右）、或者六组点集222222（从左至右）、或者五组点集22224（从左至右）等。以上情形与工字形特征有关，唯一确定是： 转角处的直角关系、以及腰部较细的特征。
五组的情形：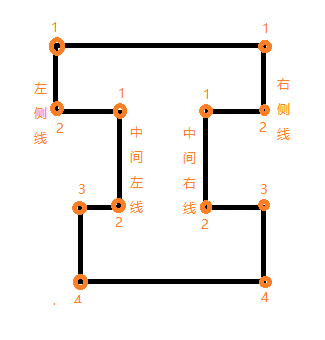
六组的情形：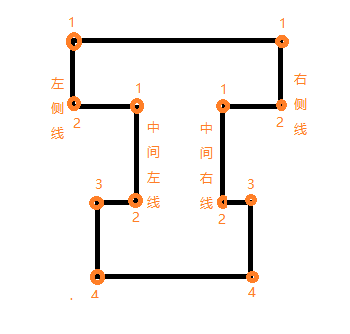
4、对每组点进行代数排序。
5、对于只有四组点的情况，只需取出2个点组的第一点，和4个点组的第二点进行排序，然后查看排序后的点组为2442排序，还是4224式的排序，即可确定这些点组是按从上至下取点（2442），还是从左到右取点（4224）。即得这四组点的空间排序。按方位取出相应点，即得顺或逆时针排列的12个点集。
6、如果得到五组或者六组，则可确定工字形侧线上下端没有对齐。单独处理相当麻烦，此时可以回到第二、3步，取这组垂线的另一个方向，必定求得四个点组，且排序必为2442的情形。然后求得12点的时针方向排序。
对以上算法，感觉还是不错的。
欢迎提出你的想法！