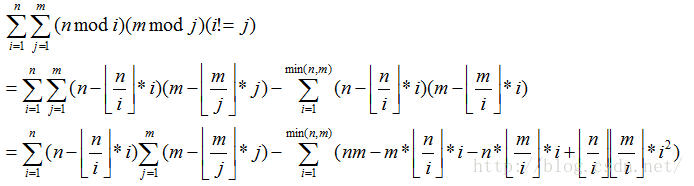第一部分
题目描述
科学家们在Samuel星球上的探险得到了丰富的能源储备,这使得空间站中大型计算机“Samuel II”的长时间运算成为了可能。由于在去年一年的辛苦工作取得了不错的成绩,小联被允许用“Samuel II”进行数学研究。
小联最近在研究和约数有关的问题,他统计每个正数N的约数的个数,并以f(N)来表示。例如12的约数有1、2、3、4、6、12。因此f(12)=6。下表给出了一些f(N)的取值:

f(n)表示n的约数个数,现在给出n,要求求出f(1)到f(n)的总和。
输入输出格式
输入格式:输入一行,一个整数n
输出格式:输出一个整数,表示总和
输入输出样例
说明
【数据范围】
20%N<=5000
100%N<=1000000
200%N<=100000000000000
1000%N<=1000000000000000000000000000000000000000000000000000000000000000(63 0's)
本题原来基本上是一个暴力
不过结论比较重要
就是∑(i=1,n)d(i)=∑(i=1,n)(n/i)
此处下取整
这样的话发现对于比如说6
求右半部分为
6 3 2 1 1 1
有三个一
这重复计算了
这样可以实现二百分算法就是数论分块、
直接贴代码就行
#include<cstdio> #include<iostream> int n,ans=0; int main(){ scanf("%d",&n); for(int i=1,j;i<=n;i=j+1){ j=n/(n/i); ans+=(n/i)*(j-i+1); } printf("%d",ans); return 0; }
代码是对的!!!!!
1000分的算法需要反演等 达到n的三分之一次方logn
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
模积和
所求就是第一行
n《=1e9;
图片是用的别人的叫qingdaobaibai,谢谢!!!
预备知识:
1.前面的那个题的内容
2.欧拉定理
3.(费马小)
4.乘法逆元
5.阿尔贝恒等式的一些知识
∑aibi=∑(k:1,n)∑(i:1,k)ai(bk-bk+1)+sabn
这里列举一下纲目 将在另一个合适的博客里写
∑ai∑bi=∑∑aibj
等
这是代码
#include<iostream> #include<cstdio> #define ll long long #define p 19940417 #define ine2 9970209 #define ine6 3323403 using namespace std; ll n,m; ll calc(ll k,ll n) { ll tmp=0; for (ll i=1,pos=0;i<=k;i=pos+1) { pos=min(n/(n/i),k); (tmp+=(n/i)%p*(((pos+1)*(pos)%p*ine2%p-(i-1)*i%p*ine2%p+p)%p)%p)%=p; } return (tmp+p)%p; } ll calc0(ll n,ll m) { ll tmp=0; for (ll i=1,pos=0;i<=n;i=pos+1) { pos=min(n/(n/i),m/(m/i)); (tmp+=(n/i)*(m/i)%p*((pos*(pos+1)%p*(pos*2+1)%p*ine6%p-(i-1)*i%p*(i*2-1)%p*ine6%p+p)%p)%p)%=p; } return (tmp+p)%p; } int main() { scanf("%lld%lld",&n,&m); if (n>m) swap(n,m); ll t1=calc(n,n),t2=calc(m,m),t3=calc(n,m),t4=calc0(n,m); ll ans=((((ll)n*n%p-t1+p)%p)*(((ll)m*m%p-t2+p)%p)%p-((ll)n*n%p*m%p-(ll)t1*m%p-(ll)t3*n%p+t4%p+p*10)%p+p)%p; cout << ans << endl; return 0; }
代码本非我打,感谢原出处的教学。
这样的话基本数论分块的两种模式就显然了