Description
Y901高速公路是一条重要的交通纽带,政府部门建设初期的投入以及使用期间的养护费用都不低,因此政府在这条高速公路上设立了许多收费站。
Y901高速公路是一条由N-1段路以及N个收费站组成的东西向的链,我们按照由西向东的顺序将收费站依次编号为1~N,从收费站i行驶到i+1(或从i+1行驶到i)需要收取Vi的费用。高速路刚建成时所有的路段都是免费的。
政府部门根据实际情况,会不定期地对连续路段的收费标准进行调整,根据政策涨价或降价。
无聊的小A同学总喜欢研究一些稀奇古怪的问题,他开车在这条高速路上行驶时想到了这样一个问题:对于给定的l,r(l<r),在第l个到第r个收费站里等概率随机取出两个不同的收费站a和b,那么从a行驶到b将期望花费多少费用呢?
Input
第一行2个正整数N,M,表示有N个收费站,M次调整或询问
接下来M行,每行将出现以下两种形式中的一种
C l r v 表示将第l个收费站到第r个收费站之间的所有道路的通行费全部增加v
Q l r 表示对于给定的l,r,要求回答小A的问题
所有C与Q操作中保证1<=l l<r,在第l个到第r个收费站里等概率随机取出两个不同的收费站a和b,那么从a行驶到b将期望花费多少费用呢?
Output
对于每次询问操作回答一行,输出一个既约分数
若答案为整数a,输出a/1
Sample Input
4 5
C 1 4 2
C 1 2 -1
Q 1 2
Q 2 4
Q 1 4
Sample Output
1/1
8/3
17/6
Hint
数据约束
所有C操作中的v的绝对值不超过10000
在任何时刻任意道路的费用均为不超过10000的非负整数
N,M<=1e5
Solution对于一次询问,第i条边的贡献为 wi*(i-L+1)*(R-i+1)
可以这么理解,在i的左边(包括自身)选择起点,在i的右边(包括自身)选择终点,相乘即为组合的个数
然后
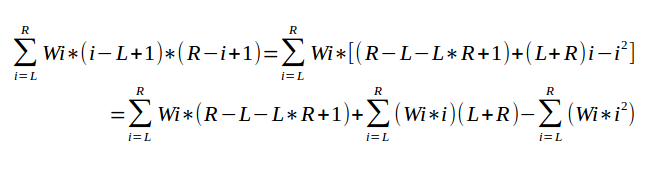
我们就可以看出,用线段树分别维护三个值:S0:∑wi , S1:∑(wi*i) , S2:∑(wi*i2)即可
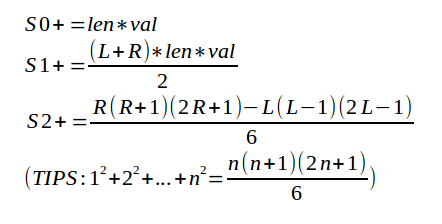 (S2漏乘了一个val)
(S2漏乘了一个val)
这个该死的线段树调了我两个小时。以后打线段树还是要小心一点慢点打 = =
Code

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #define RG register int 6 #define rep(i,a,b) for(RG i=a;i<=b;i++) 7 #define per(i,a,b) for(RG i=a;i>=b;i--) 8 #define inf (1<<30) 9 #define maxn 100005 10 #define ll long long 11 #define ls pos<<1 12 #define rs pos<<1|1 13 #define L t[pos].l 14 #define R t[pos].r 15 #define mid ((t[pos].l+t[pos].r)>>1) 16 #define cal0(x,y) x*y 17 #define cal1(x,y,z,w) (x+y)*z*w/2ll 18 #define cal2(x,y,z) (y*(y+1ll)*(2ll*y+1ll)-x*(x-1ll)*(2ll*x-1ll))*z/6ll //bug 19 using namespace std; 20 int n,m; 21 struct T{ 22 int l,r; 23 ll s0,s1,s2,tag; 24 }t[maxn<<2]; 25 struct Dat{ 26 ll a0,a1,a2; 27 inline Dat operator + (const Dat x)const{ 28 return (Dat){a0+x.a0,a1+x.a1,a2+x.a2}; 29 } 30 }; 31 inline int read() 32 { 33 int x=0,f=1;char c=getchar(); 34 while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} 35 while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} 36 return x*f; 37 } 38 39 void build(int pos,int l,int r) 40 { 41 t[pos].l=l,t[pos].r=r; 42 if(l==r) return; 43 build(ls,l,mid);build(rs,mid+1,r); 44 } 45 46 inline void pushdown(int pos) 47 { 48 t[ls].tag+=t[pos].tag,t[rs].tag+=t[pos].tag; 49 ll len1=t[ls].r-t[ls].l+1,len2=t[rs].r-t[rs].l+1;//bug 50 51 t[ls].s0+=cal0(len1,t[pos].tag), 52 t[ls].s1+=cal1(t[ls].l,t[ls].r,len1,t[pos].tag), 53 t[ls].s2+=cal2(t[ls].l,t[ls].r,t[pos].tag); 54 55 t[rs].s0+=cal0(len2,t[pos].tag), 56 t[rs].s1+=cal1(t[rs].l,t[rs].r,len2,t[pos].tag), 57 t[rs].s2+=cal2(t[rs].l,t[rs].r,t[pos].tag); 58 59 t[pos].tag=0; 60 } 61 62 void update(int pos,int l,int r,ll val) 63 { 64 if(l<=L&&R<=r) 65 { 66 ll len=R-L+1; 67 t[pos].s0+=cal0(len,val), 68 t[pos].s1+=cal1(L,R,len,val), 69 t[pos].s2+=cal2(L,R,val); 70 t[pos].tag+=val; 71 return; 72 } 73 if(t[pos].tag) pushdown(pos); 74 if(l<=mid) update(ls,l,r,val);//bug 75 if(r>mid) update(rs,l,r,val);//bug 76 t[pos].s0=t[ls].s0+t[rs].s0, 77 t[pos].s1=t[ls].s1+t[rs].s1, 78 t[pos].s2=t[ls].s2+t[rs].s2; 79 } 80 81 Dat query(int pos,int l,int r) 82 { 83 if(l<=t[pos].l&&t[pos].r<=r) 84 return (Dat){t[pos].s0,t[pos].s1,t[pos].s2}; 85 if(t[pos].tag) pushdown(pos); 86 Dat ans=(Dat){0,0,0}; 87 if(l<=mid) ans=query(ls,l,r); 88 if(r>mid) ans=ans+query(rs,l,r); 89 return ans; 90 } 91 92 ll gcd(ll a,ll b){return (!(a%b)?b:gcd(b,a%b));} 93 94 int main() 95 { 96 n=read(),m=read(); 97 build(1,1,n-1); 98 char opt[3]; 99 register ll l,r,v; 100 rep(i,1,m) 101 { 102 scanf("%s",opt); 103 if(opt[0]=='C') 104 { 105 l=read(),r=read()-1,v=read(); 106 update(1,l,r,v); 107 } 108 else 109 { 110 l=read(),r=read()-1; 111 Dat ans=query(1,l,r); 112 ll up=ans.a0*(r-l-l*r+1ll)+ans.a1*(l+r)-ans.a2; 113 ll down=(r-l+1ll)*(r-l+2ll)/2ll; 114 ll gd=gcd(up,down); 115 up/=gd,down/=gd; 116 printf("%lld/%lld ",up,down); 117 } 118 } 119 return 0; 120 }
