【问题描述】
小洪喜欢区间,他有一个宏大的区间游戏。
小洪有一个集合S(初始为空),然后,小洪会依次对这个区间做一些操作,操作分为5种,5种操作以及集合之间的运算规则如下:
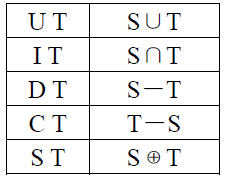
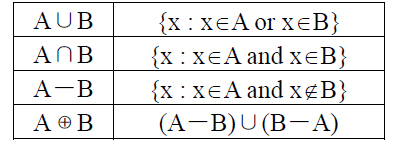
wangy是小洪的粉丝,他想知道经过这些操作后的最终集合S。但他实在是太弱了,于是他找到了你,请你帮他解决这个问题。
【输入格式】
输入共m行,每行描述一个操作。
每行的格式为O T,用一个空格隔开。O表示运算的种类,T为一个区间。区间用(a,b), (a,b], [a,b), [a,b]表示。
保证输入数据中没有多余的空格。
【输出格式】
输出一行若干个用空格分开的区间,描述最终的集合S。你需要保证你输出的所有区间交集为空,并集为最终的S,并且你需要将它们按左端点从小到大排序。
特别地,如果最终的集合S为空集,则输出一行”empty set”(不含引号)。
【输入输出样例】
|
interval1.in
|
interval1.out
|
|
U [1,5]
D [3,3]
S [2,4]
C (1,5)
I (2,3]
U [4,6)
|
(2,3) [4,6)
|
|
interval2.in
|
interval2.out
|
|
S [3,5]
S [3,5]
|
empty set
|
【数据规模】
|
测试点编号
|
m
|
a,b
|
备注
|
|
1-3
|
n≤100
|
a,b≤255
|
|
|
4-6
|
所有区间为闭区间
|
||
|
7-8
|
n≤10001
|
a,b≤65535
|
|
|
9-12
|
n≤40000
|
||
|
13-15
|
n≤10001
|
|
|
|
16-19
|
n≤40000
|
|
|
|
20-25
|
n≤200000
|
a,b≤262143
|
|
对于所有的数据,保证m>0,0≤a≤b。保证输入数据中的所有区间均不为空。
考虑维护一棵权值线段树,中括号和小括号不好处理。
我们将值域*2,那么小括号对应奇数,中括号对应偶数。
线段树要支持区间赋值和区间取反的操作,注意空格输出空格。
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define lim 524287 4 #define M 1500010 5 int q[M]; 6 inline void Do(int o) { 7 if(q[o] == 1 || q[o] == -1) { 8 q[2 * o] = q[2 * o + 1] = q[o]; 9 } 10 if(q[o] == 2) { 11 q[2 * o] = -q[2 * o]; 12 q[2 * o + 1] = -q[2 * o + 1]; 13 } 14 q[o] = -2; 15 } 16 inline void Add(int l, int r, int o, int x, int y, int z) { 17 if(x <= l && r <= y) { 18 q[o] = z; 19 return; 20 } 21 int mid = (l + r) / 2; 22 Do(o); 23 if(x <= mid) Add(l, mid, 2 * o, x, y, z); 24 if(y > mid) Add(mid + 1, r, 2 * o + 1, x, y, z); 25 } 26 inline void rev(int l, int r, int o, int x, int y) { 27 if(x <= l && r <= y) { 28 q[o] = -q[o]; 29 return; 30 } 31 int mid = (l + r) / 2; 32 Do(o); 33 if(x <= mid) rev(l, mid, 2 * o, x, y); 34 if(y > mid) rev(mid + 1, r, 2 * o + 1, x, y); 35 } 36 inline void pd(int l, int r, int o) { 37 if(l == r) return; 38 int mid = (l + r) / 2; 39 Do(o); 40 pd(l, mid, 2 * o); 41 pd(mid + 1, r, 2 * o + 1); 42 } 43 int main() { 44 char s[10]; 45 memset(q, -1, sizeof(q)); 46 while(scanf("%s", s) != EOF) { 47 char A, B; 48 int l, r; 49 A = getchar(); 50 while(A != '(' && A != '[') A = getchar(); 51 scanf("%d,%d", &l, &r); 52 B = getchar(); 53 while(B != ')' && B != ']') B = getchar(); 54 l = l * 2 + (A == '('); 55 r = r * 2 - (B == ')'); 56 if(s[0] == 'U') { 57 Add(0, lim, 1, l, r, 1); 58 } 59 else if(s[0] == 'I') { 60 if(l) Add(0, lim, 1, 0, l - 1, -1); 61 Add(0, lim, 1, r + 1, lim, -1); 62 } 63 else if(s[0] == 'D') { 64 Add(0, lim, 1, l, r, -1); 65 } 66 else if(s[0] == 'C') { 67 if(l) Add(0, lim, 1, 0, l - 1, -1); 68 Add(0, lim, 1, r + 1, lim, -1); 69 rev(0, lim, 1, l, r); 70 } 71 else { 72 rev(0, lim, 1, l, r); 73 } 74 } 75 pd(0, lim, 1); 76 q[lim] = -1; 77 bool flag = false; 78 for(int i = 0; i <= lim; ++ i) { 79 if(q[lim + i] == -1 && q[i + lim + 1] == 1) { 80 if(flag) printf(" "); 81 if(i & 1) printf("("); 82 else printf("["); 83 printf("%d,", i / 2); 84 flag = true; 85 } 86 if(q[lim + i] == 1 && q[i + lim + 1] == -1) { 87 printf("%d", i / 2); 88 if(i & 1) printf("]"); 89 else printf(")"); 90 } 91 } 92 if(!flag) puts("empty set"); 93 }