在数学最优化问题中,拉格朗日乘数法(以数学家约瑟夫·路易斯·拉格朗日命名)是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题,其变量不受任何约束。这种方法引入了一种新的标量未知数,即拉格朗日乘数:约束方程的梯度(gradient)的线性组合里每个矢量的系数。
简单举例:
- 求
 的极值
的极值 - 条件

引入新变量拉格朗日乘数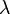 ,即可求解下列拉格朗日方程
,即可求解下列拉格朗日方程
此方法的证明牵涉到偏微分,全微分或链法,从而找到能让设出的隐函数的微分为零的未知数的值。
-----------------------------
介绍先看一个二维的例子:假设有函数:f(x,y),要求其极值(最大值/最小值),且
c 为常数。对不同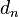 的值,不难想像出
的值,不难想像出
的等高线。而方程 的等高线正好是
的等高线正好是 。想像我们沿着
。想像我们沿着 的等高线走;因为大部分情况下
的等高线走;因为大部分情况下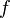 和
和 的等高线不会重合,但在有解的情况下,这两条线会相交。想像此时我们移动
的等高线不会重合,但在有解的情况下,这两条线会相交。想像此时我们移动 上的点,因为
上的点,因为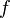 是连续的方程,我们因此能走到
是连续的方程,我们因此能走到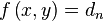 更高或更低的等高线上,也就是说
更高或更低的等高线上,也就是说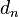 可以变大或变小。只有当
可以变大或变小。只有当 和
和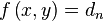 相切,也就是说,此时,我们正同时沿着
相切,也就是说,此时,我们正同时沿着 和
和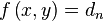 走。这种情况下,会出现极值或鞍点。
走。这种情况下,会出现极值或鞍点。
气象图中就很常出现这样的例子,当温度和气压两列等高线同时出现的时候,切点就意味着约束极值的存在。
用矢量的形式来表达的话,我们说相切的性质在此意味着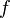 和
和 的斜率在某点上平行。此时引入一个未知标量λ,并求解:
的斜率在某点上平行。此时引入一个未知标量λ,并求解:
且λ ≠ 0.
一旦求出λ的值,将其套入下式,易求在无约束极值和极值所对应的点。
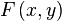 =
= 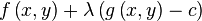
新方程 在达到极值时与
在达到极值时与 相等,因为
相等,因为 达到极值时
达到极值时 总等于零。
总等于零。
求此方程的最大值:
同时未知数满足
因为只有一个未知数的限制条件,我们只需要用一个乘数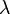 .
.
将所有 方程的偏微分设为零,得到一个方程组,最大值是以下方程组的解中的一个:
方程的偏微分设为零,得到一个方程组,最大值是以下方程组的解中的一个:
http://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E6%95%B0










