从有理数到实数和数的连续体

本文主要是想通过简单易懂且兼顾严谨性的方式来介绍如何从有理数过渡到实数。文章稍长，但看完后你至少会明白如下几个关键问题：

1. 无理数或实数的定义；

2. 实数集为什么是连续的、实数集里的数为什么可以和数轴上的点一一对应；

3. 无理数的独特性质；

4. 无理数为什么也满足有理数的运算法则和运算性质（如乘法结合律、分配律等）；

另外，本文引证了一些英文叙述，看不懂并无大碍，理解我的中文叙述才是重点。

第一部分 从有理数集到连续的实数集

首先我们来看如何把所有的有理数表示在一条直线上。当在一条水平直线上选定代表0和1的点之后（0在1的左边），把0和1间的距离叫作单位长度，在1的右边每隔一个单位长度就取一个点，一直无止境地进行下去，把这些新标示出来的点从左到右依次用来代表2，3，4......这些正整数，在0的左边每隔一个单位长度就取一个点，一直无止境地进行下去，把这些新标示出来的点从右到左依次用来代表-1，-2，-3，......这些负整数，这样我们就在这条直线上找到了代表每个整数（分母为1的有理数）的点，可以通过尺规作图来完成这种构造。每个有理数都可以用(frac{p}{q})这种形式唯一表示，这里(p)是正整数，并且(p)和(q)没有比1大的公因子，为了在这条直线上标出代表分母(mathbf{q})大于1的有理数的点，我们只需把每个单位长度的区间进行(q)等分（尺规作图可以做到这一点），那么每一个分点就都代表一个分母为(q)的有理数。显然每个有理数都可以用这种方法在这条直线上找到代表它的那个点，可称这些点为"有理点"，但是一个很重要的事实是——并非这条直线上的所有点都是有理点，比如直角边为单位长度的等腰直角三角形，如果用圆规以其斜边长为半径，代表0的点为圆心画圆的话，那么圆弧与这条直线的交点就不会与任何有理点重合^[1]。

证明：设其斜边长度为(l)，那么根据勾股定理有(l^{2} = 1^{2} + 1^{2} = 2)，如果那个交点是有理点，那么(l)就应该是一个有理数，则(l)可以用(frac{p}{q})这种形式唯一表示，即(l = frac{p}{q})，按规定(p)和(q)没有比1大的公因子，把(l)换成(frac{p}{q})后有(({frac{p}{q})}^{2} = 2)，接下来我们将导出与此相悖的结论出来。稍作变换得到(p^{2} = 2q^{2})，那么(p^{2})就是偶数了，显然(p)也必须是偶数，便有(p = 2p_{0})，(p_{0})是整数，把前面等式的(p)换作(2p_{0})后有(4p_{0}^{2} = 2q^{2})，即(2p_{0}^{2} = q^{2})，这说明(q^{2})是偶数，显然(q)也必须是偶数，这就证明了(p)和(q)有公因子2，这与前面的"(p)和(q)没有比1大的公因子"这个规定矛盾，而造成这种矛盾的起因就是我们一开始假设那个交点是有理点，所以数轴上的点并非都有有理数与之对应，可称没有有理数与之对应的点为"无理点"，很容易能在数轴上构造出无数多个无理点出来。

显然，如果我们需要用数来表示所有线段的长度的话，那么我们必须接受下面这条事实：水平直线上的每个无理点都应该要有唯一的非有理数与之对应，可称这个数为"无理数"，并且如果一个无理点在另外一点的右边（或左边），那么与这个无理点对应的无理数大于（或小于）与那个别的点对应的数。可把有理数和无理数统称为实数，把这条每个点都对应唯一一个实数的直线称为数轴，这样实数就和数轴上的点一一对应了。另外需要注意的是并非每个无理数都可以用尺规作图这种方式找出其在这条直线上所对应的点^[2]。

直线是连续的，其连续性表现出了这样的性质^[3]：如果把一条水平直线上的所有点分成左右两个部分，左边这部分的每一点都在右边这部分的每一点的左边，那么有且仅有一个点能造成这种分割，这个点本身可以归为左边这部分的最后一点或右边这部分的起点。这条性质是由德国数学家戴德金（Richard Dedekind）提出的，他认为这条性质是一个明显的事实，无需也无法被证明，它能够刻画直线的连续性，它是直线之所以连续的本质表现，应将其看作一条公理^[4]，可称其为直线连续性公理（line continuity axiom）。需要说明的一点是这条公理默认运用了"直线上两个不同点间存在无数多个不同点"这条性质，因为如果至少有两个不同点可以把直线分成同样的左边和右边两部分，那么这两个点间的那无数多个点既不属于左边的部分也不属于右边的部分，基于此，公理中才说"有且仅有一个点能造成这种分割"。

因为实数集里的实数可以铺满直线并且和直线上的点一一对应，直线具有连续性，那么这个实数集也应该具备相应的连续性。Dedekind从直线连续性公理得到启示，认为实数集的连续性应该表现出这样的性质：如果把实数集内的所有数分成两部分(A_{1})和(A_{2})，以至于(A_{1})内的每个数都小于(A_{2})内的每个数，那么有且仅有一个数能产生这个分割，这个数本身可以归为(A_{1})这部分的最大数或(A_{2})这部分的最小数^[5]。实数集是连续的，所以也称实数集是数的连续体，英文number continuum^[6]，亦译作"数的连续统"。上面这条性质可称为数的连续体公理（number continuum axiom），因为这条性质是受直线连续性公理启示而提出来的，所以也应将它看成是一个给定的事实，无需证明。

至此，你也许会高呼："好了！我们终于有数的连续体了！"但是，我们还是必须得摸清楚这个连续体内的情况、搞清楚它具备的其它性质才行，不然空有一个概念而不懂其性质，那么我们也就无法运用数的连续体，最终也只不过是让这个概念形同虚设，无所用场。

有需要的读者请先去了解实数集的这些概念以便继续阅读：上界、最小上界（亦作"上确界"，英文the least upper bound）、下界、最大下界（亦作"下确界"，英文the greater lower bound）。

要学习的首条性质很重要，它使得实数集区别于有理数集------非空有上界的实数集在实数集内有最小上界（上确界）^[7]，称为实数集的最小上界性质（Least upper bound property of R）。

证明：设A是(mathbb{R})的非空真子集且有上界，那么比A内每个数都大的实数组成的集合C，余下的实数组成的集合B内的每个数都小于C内的每个数，根据数的连续体公理可知有且仅有一个实数c能把实数集分成B和C两部分，c是B的最小上界。另外因为集合B内的每个数都不比A内每个数都大，所以A的上界就是B的上界，又因为A⊂B，所以B的上界就是A的上界，综上可知集合A和集合B有共同的最小上界c，所以有上界的集合A在实数集内有最小上界。

反过来看，如果非空有上界的实数集A在实数集内有最小上界c的话，那么不大于c的数组成的集合B包含集合A，大于c的数组成集合C，这样实数集就被分成了集合B和C，B里的数都小于C里的数，显然c就是唯一产生这个分割的数。可见，数的连续体公理和实数集最小上界性质可互相导出彼此，也就是它们是等价的，当然，如果我们以实数集最小上界性质作为公理的话，那么"数的连续体公理"可以由其推得，就应该把它改名作"数的连续体定理"了，因为我们要求公理是不需要证明的。忽略称谓上区别的问题，我们应该记住的是这两条性质是等价的，很多书上都以实数集最小上界性质作为刻画实数集连续的根本性质，其也被称为完整性（或完备性）公理（或定理）（completeness axiom 或completeness theorem），同样，至于叫它公理还是定理取决于是否将这条性质看作是给定的事实。

非空有上界的有理数集在有理数集内就未必有最小上界，此处举例说明。因为没有平方等于2的有理数，所以可把有理数分成所有负有理数和平方小于2的非负有理数组成的集合(A_{1} = { x in mathbb{Q}|x^{2} < 2mathrm{ }mathrm{ ext{or}}mathrm{ }x < 0})和所有平方大于2的正有理数组成的集合(A_{2} = { x in mathbb{Q}|x^{2} > 2mathrm{ }mathrm{ ext{and}}mathrm{ }x > 0})，如果我们在有理数集内讨论(A_{1})的最小上界的话，那么因为此前文章我们已经证明过中无最大数， 所以这个最小上界只可能在(A_{2})内，如果在(A_{2})内有(A_{1})的最小上界c的话，那么根据已经证明过的(A_{2})中无最小数可知(A_{2})内有比c更小的有理数b，b仍然大于(A_{1})内的所有数，所以(A_{1})在(A_{2})内无最小上界，总之(A_{1})在有理数集内都没有最小上界，由此可见有上界的有理数集在有理数集内不一定有最小上界，所以说实数集的最小上界性质使得实数集区别于有理数集，而造成这种状况的根本原因还是实数集是连续的而有理数集却不然。

根据实数集的最小上界性质我们可以证明实数集的阿基米德性质（Archimedean Property for Real Numbers）：如果x和y都是任意正实数，那么存在正整数n使得nx > y.

可用反证法来证明：假设nx > y对于任何正整数n都不成立，那么也就是说集合A={nx|n∈N}有上界y。根据实数集的最小上界性质可知A有最小上界z，因为x是正数，所以z-x就不是A的上界，那么也就存在正整数m使得mx>z-x，该式变形可得（m+1）x>z，也就是A中的元素（m+1）x大于A的最小上界，这是不可能的，所以原结论得证^[8]。

根据实数集的阿基米德性质可得到如下两条性质：

1）对于任意正实数x，总存在正整数n使得(frac{1}{n} < x)。

将不等式两边都乘以n得到1<nx，这个不等式是符合实数集的阿基米德性质的，故得证。这个证明过程中需要读者接受这个不等性质：如果x<y，对于任意正整数n有nx<ny。通过实数集的阿基米德性质和本条性质可知：实数集内即无最大正数也无最小正数。

2）如果(a)和(b)都是实数并且(a < b)，那么必存在有理数(r)使得(a < r < b) 。^[9]

证明：1和(b - a)都是正实数，那么必存在正整数(n)使得(nleft( b - a ight) > 1)。因为差值大于1的两实数间必然存在整数(m)，所以有(nb > m > na)，稍作变形得到(b > frac{m}{n} > a)，显然(frac{m}{n})是有理数，所以任何两个不相等的实数间存在有理数，重复应用这个的方法我们还可以得到任何两个不相等的实数间存在无数个有理数这个结论(请读者思考其中的证明细节)。这个证明过程用到了实数的乘法分配律，即：(nleft( b - a ight) = nb - na)，需要读者接受分配律是对的此证明才成立。

上面说到的实数集的性质都很关键，请读者留意！首次学习微积分（国内称为"高等数学"）或数学分析的学生掌握上面这些性质，然后再加上大学之前的数学课程里学习到的和实数相关的不等关系和算术运算法则，对于学习这两门课程就差不多了，下面的内容是为想要进一步了解实数理论的学生写的。

第二部分 定义实数的方式

现在我们来回顾一下实数集的得出过程。从有理数集扩展到实数集需要引入的是一类新的数——无理数，所以问题就归结到如何去得出无理数、如何去定义无理数。不同于本文中的无理数的定义方式——与一个无理点唯一对应的数，现在比较盛行的无理数或实数的定义方法分别是德国数学家康托（Georg Cantor）的和Dedekind的方法。因为无理数集被视为实数集的一部分，所以当有了实数的定义方法时，无理数的定义方法自然就可以用实数的定义方法来代替，因此下文主要说的是实数的定义方法。

Cantor对实数的定义^[10]是：对于任意给定的有理数，如果一个各项都是有理数的数列去除有限多项外的其它无限多项间的差值都小于这个有理数，那么这个数列就是一个实数。

现在大多数教材普遍认为Dedekind对实数的定义^[11]是：每一个有理数集的分割就是一个实数。有理数集分割的定义是：把有理数集分成两个非空集合(A_{1})和(A_{2})，以至对于(a_{1} in A_{1})和(a_{2} in A_{2})，有(a_{1} < a_{2})，Dedekind把这种分法称为分割（Cut），后人称其为有理数集的Dedekind分割（Dedekind Cut），记为(A_{1}|A_{2})。我认为这种实数定义与Dedekind的原意有所不同，后文会详细说明原因。

当你第一次看到这些实数定义时，你也许会像我一样痛苦地感叹道：这是什么东西？如此怪异，完全看不懂啊！我们为什么需要这种令人费解的定义？按照他们这些定义来描述实数，那么实数到底是个什么东西啊？完全没有了我们一开始对实数认识的样子了。之前我们可以直观地认为实数就是数轴上的第一个点，但现在，实数从我们自认为最熟悉的数变成了难以捉摸、令人费解的怪物！

实数的概念（包括有理数和无理数）在这两种定义出现之前就已经存在了，但是因为一直没有对实数有个明确的定义，以至于这种模糊的概念造成了很多矛盾，比如曾经一度认为实数集里包含所谓的"无穷小数"和"无穷大数"。上面这两种实数定义提出的目的是为了给实数一个严格的定义，为实数的存在建立严谨的基础，进而排出之前模糊不清的实数概念所带来的矛盾。总之，这两种实数定义是数学家在对实数有了基本的直观的认识之后对实数进行严谨的正式的整理之后的产物^[12]，这些定义为的是严谨，至于是否让初学者觉得简单易学并不是这些定义主要关心的问题，关于数学知识的严谨性与可理解性、可学性的探讨读者可以看看Morris Kline的 Calculus: An Intuitive and Physical Approach(Second Edition)的preface to the first edition部分，作者对微积分的教学和它的严谨性间的关系有着非常有见地的认识！另外一个让初学者觉得这两种实数定义难以理解的主要原因是这两种定义都用抛弃几何的方法去定义实数，进而给出的实数定义比较抽象和怪异。德国数学家Hermann Hankel对此评论说："这类抛弃了几何连续体（直线）启示而定义出来的实数尽管有了严谨的基础，但却是极端晦涩难懂、令人反感畏惧的人造物，每个人都有权利去怀疑这些定义的科学价值。"原话^[13]： Every attempt to treat the irrational numbers formally and without the concept of (geometric) magnitude must lead to the most abstruse and troublesome artificialities, which, even if they can be carried through with complete rigor, as we have every right to doubt, do not have a higher scientific value.

对于大多数想要弄清楚"实数集为什么是连续的"、"实数和数轴上的点为什么是一一对应的"的初学者来说，这种抛弃几何直观后给实数的定义已经把他们对实数的印象搞得面目全非了，如果还要按照这种路子走下去，那么后续的学习很大程度上只是应用这些定义或性质去机械地证明一些结论，对于理解背后的数学思想基本没什么实质性的帮助。德国数学家Paul du Bois-Reymond也表达了和我同样的观点——剥离了实数和几何连续体（直线）关系后建立的分析学将会使得这门学科沦为折腾符号的玩意儿。原话^[14]：A purely formalistic-literal framework of analysis which is what the separation of number from magnitude amounts to, would degrade this science to a mere game of symbols.

不管这些定义的创建者避免使用几何方法来定义实数的原因为何，一个很迫切很关键的需求是：我们需要每条线段的长度都要能用一个数去代表去衡量，换句话说就是要有一个数集以至于这里面的每个数和直线上每个点一一对应，这是一种迫切的要求，这必然使得我们把"要有一个数集以至于这里面的每个数和直线上的每个点一一对应"当作是一条必须成立的性质——把它看作是一条公理，这个数集就是实数集，实际上即便是上面这两种定义的提出者Cantor和Dedekind——他们用抛弃了几何的方法去定义实数，但是为了在"数（特指实数集）"和"形（特指直线）"之间建立联系也不得不引入这条公理^[15]，后世称之为Cantor-Dedekind公理^[16]------直线上的每个点和和实数集里的实数一一对应。正是基于数和形之间无法割舍的紧密关系，也因为抛弃几何后对实数下的定义非常抽象和怪异、不易理解，所以本文的无理数的定义方式并没有抛弃几何，而是把无理数定义为与一个无理点唯一对应的数。

第三部分 回顾Dedekind对实数的定义方式

现在我们来看看Dedekind对实数的定义方式，这有助于我们进一步了解实数的性质。Dedekind是从上文提到的直线连续性公理出发，以有理数集为基础来构造数的连续体的。他首先引入了一种有理数集的分割方式——把有理数集(mathbb{Q})分成两个非空集合(A_{1})和(A_{2})，也就有(A_{1} cup A_{2} = mathbb{Q})，另外对于(a_{1} in A_{1})和(a_{2} in A_{2})，有(a_{1} < a_{2})。后人将这种分割方式命名为有理数集的Dedekind分割（Dedekind Cut），记为(A_{1}|A_{2})。

有理数集的Dedekind分割(A_{1}|A_{2})不外乎就是这3种情况^[17]：

1）(A_{1})中有最大数，(A_{2})中无最小数，如(A_{1} = { x in mathbb{Q}|x leq a,a in mathbb{Q}})，(A_{2} = { x in mathbb{Q}|x > a,a in mathbb{Q}})；

2）(A_{1})中无最大数，(A_{2})中有最小数，如(A_{1} = { x in mathbb{Q}|x < b,b in mathbb{Q}})，(A_{2} = { x in mathbb{Q}|x geq b,b in mathbb{Q}})；

3）(A_{1})中无最大数，(A_{2})中无最小数；

"(A_{1})中有最大数(a_{1})，(A_{2})中有最小数(a_{2})"的情况是不可能的，否则(frac{a_{1} + a_{2}}{2})便是一个不在(A_{1} cup A_{2})内的有理数，这与(A_{1} cup A_{2} = mathbb{Q})相悖。

上面的第三种情况是值得我们仔细思考的。第三种分割可能存在吗？存在！上文提到的所有负有理数和平方小于2的非负有理数组成的集合(A_{1} = { x in mathbb{Q}|x^{2} < 2mathrm{ }mathrm{ ext{or}}mathrm{ }x < 0})和所有平方大于2的正有理数组成的集合(A_{2} = { x in mathbb{Q}|x^{2} > 2mathrm{ }mathrm{ ext{and}}mathrm{ }x > 0})构成的分割(A_{1}|A_{2})就符合第三种情况。实际上这种分割有无数多个，比如让D是任意一个正整数并且(sqrt{D})不是正整数^[18]，那么(A_{1} = { x in mathbb{Q}|x^{2} < Dmathrm{ }mathrm{ ext{or}}mathrm{ }x < 0})和(A_{2} = { x in mathbb{Q}|x^{2} > Dmathrm{ }mathrm{ ext{and}}mathrm{ }x > 0})构成的分割同样是(A_{1})中无最大数，(A_{2})中无最小数。第一种情况下的分割可以看作是由(A_{1})里的(a)产生的，第二种情况下的分割可以看作是由(A_{2})里的(b)产生的，至于第三种情况下的分割，对于任何一个(A_{1})或(A_{2})中的数在同一集合内都有比它大或小的有理数，所以任何一个(A_{1})或(A_{2})中的数都不可能产生这种情况下的分割，因此这个分割不是由有理数来产生，Dedekind说这个分割是由一个新的数——无理数来产生的，他的原话是这么说的^[19]：Whenever, then, we have to do with a cut (A_{1}|A_{2}) produced by no rational number, we create a new, an irrational number α, which we regard as completely defined by this cut (A_{1}|A_{2}); we shall say that the number α corresponds to this cut, or that it produces this cut. From now on, therefore, to every definite cut there corresponds a definite rational or irrational number, and we regard two numbers as different or unequal always and only when they correspond to essentially different cuts.

Dedekind从有理数集出发，通过定义分割的方式最终得到的只不过是有理数集和有理数集的分割而已，并没有所谓的"无理数"这种新概念，如果有的话，那么这个概念也只不过是"不是由有理数产生的分割"的别名罢了，或者说无理数就是这种分割，并不能说分割是由无理数产生的，如果硬是要这么说那就默认假定了"无理数"和"不是由有理数产生的分割"是不同的概念了，那么这个"无理数"又是哪里来的呢？这个问题在1888年就由德国数学家Heinrich Weber写信告诉过Dedekind，但Dedekind回答说：我定义的无理数并不是"没有有理数产生的分割"，而是造成这种分割的数，正如有理数可以产生有理数集的分割并且产生分割的有理数本身并不是一个分割那样，我们完全有智力可以创造出这种区别于分割的无理数出来"------取自Morris Kline的书^[20]，原文：In fact Heinrich Weber told Dedekind this, and in a letter of 1888 Dedekind replied that the irrational number α is not the cut itself but is something distinct, which corresponds to the cut and which brings about the cut. Likewise, while the rational numbers generate cuts, they are not the same as the cuts. He says we have the mental power to create such concepts.

"我们完全有智力可以创造出这种区别于分割的无理数出来"，Dedekind的这种辩护犹如空中楼阁，他要创造区别于"不是由有理数产生的分割"的"无理数"出来是完全没有基础的。另外一个我发现的问题是：如果按照Dedekind的话说"不是由有理数产生的分割是由一个无理数产生的"，Dedekind在他的著作里并没有说明为什么这个分割不可能是由多个无理数产生的。正是因为前面第一个问题，所以现在的数学教材里介绍用有理数集的Dedekind分割构建实数集时都拒绝"不是由有理数产生的分割是由无理数产生的"这种说法，而是把实数集看成是所有有理数分割的集合，在这里面无理数是"不是由有理数产生的分割"，而有理数的定义也早已不是"可以写成(frac{p}{q})形式的数"了，而是一个"由有理数产生的有理数集的分割"，可见这种定义虽然严谨了实数理论，但是却让实数变得好不自然、比较抽象，完全颠覆了我们一开始对实数的认识，希望深入了解这种定义方式的读者可去看D.C. Goldrei的 Classic Set Theory: For Guided Independent Study，从第二章看起。本文的无理数的构造方法和Dedekind的方法一样都是受到了直线连续公理的启示而生，所不同的是本文没有把无理数看作是产生"没有有理数产生的有理数集分割"的数，而是把无理数规定为与无理点一一对应的数，这样的好处是即保留了我们对实数的直观认识，也避免了Dedekind的方法受到的质询。

另外，从本文无理数的定义角度来看，如果一个有理数集的分割(A_{1}|A_{2})不是由有理数产生的，那么这个分割确实是由一个无理数产生的，理由如下：比(A_{1})内每个数都大的实数组成的集合C（显然C包含(A_{2})），余下的实数组成的集合B（显然B包含(A_{1})）内的每个数都小于C内的每个数，根据数的连续体公理可知有且仅有一个实数c能把实数集分成B和C两部分，c是B的最小上界（显然c是个无理数，否则与“分割(A_{1}|A_{2})不是由有理数产生的”相悖）。另外因为集合B内的每个数都不比(A_{1})内的每个数都大，所以(A_{1})的上界就是B的上界，又因为(A_{1})⊂B，所以B的上界就是(A_{1})的上界，综上可知集合(A_{1})和集合B有共同的最小上界c，可见虽然(A_{1})在有理数集内没有最小上界，但是在实数集内就有最小上界。上面我们只是说到有且仅有一个无理数c能把实数集分成B和C两部分，c这个无理数也能把有理数集分作(A_{1})和(A_{2})这两个集合，那么还有没有异于c的其它无理数可以产生同样的有理数集的分割呢？如果至少有一个异于c的无理数d能产生这个有理数集的分割的话，那么根据之前已经证明过的结论知道必有有理数落在c和d之间，这与c和d能产生相同的有理数集分割相悖，所以有且仅有一个无理数能产生不是由有理数产生的有理数集分割。用同样的方法也可以证明那些由有理数产生的分割也是仅由唯一的那个有理数产生的。总之，产生有理数集分割的实数是唯一的——不可能由两个不同的实数产生相同的有理数集分割，换句话说有理数集的分割与实数是一一对应的。

没有有理数来产生的分割的存在，从数的连续体公理角度来看，这揭示了有理数集是有空隙的。因为在实数集内有且仅有一个无理数c能产生这个分割，可以说(A_{1})和(A_{2})间的空隙仅能容纳c这个无理数或者说(A_{1})和(A_{2})间的空隙被c这个无理数给填起来了，显然c大于(A_{1})内的每个有理数同时又小于(A_{2})内的每个有理数，也可以说(A_{1})和(A_{2})这两个集合可以界定c这个无理数。归根结底，这个特性还是由数的连续体或实数集的连续性所致。

我们已经知道两个有理数(frac{p_{1}}{q_{1}})和(frac{p_{2}}{q_{2}})相加的结果被定义成(frac{{p_{1}q_{2} + p}_{2}q_{1}}{{q_{1}q}_{2}})，但是因为无理数不能写成(frac{p}{q})这种形式，那么在实数集里无理数和另外一个有理数或无理数的运算结果该怎么定义呢？我们已经知道每个无理数或实数都有唯一的有理数集分割与之对应，所以可以通过有理数集的分割去探讨无理数或实数的相关问题。设(a)是产生有理数集分割(A_{1}|A_{2})的实数，b是产生有理数集分割(B_{1}|B_{2})的实数，那么对于任意一个来自(A_{1})内的有理数(a_{1})和任意一个来自(B_{1})内的有理数(b_{1})，有({a geq a}_{1})和({b geq b}_{1})，那么(a + b geq a_{1} + b_{1}),即(a + b)是(C_{1} = left{ a_{1} + b_{1} middle| a_{1}epsilon A_{1},b_{1}epsilon B_{1} ight})的上界，把其余比(C_{1})内每个有理数都大的有理数组成的集合记为(C_{2})，这样就得到了有理数集的分割(C_{1}|C_{2})，在实数集内有且仅有一个实数c能够造成这个分割。另外，因为(a + b)是(C_{1})的上界，如果我们能证明(a + b)不大于(C_{2})内的任何有理数，那么也就证明了(a + b)是产生分割(C_{1}|C_{2})的数，就有(a + b = c)，也就是说我打算用这种构造分割(C_{1}|C_{2})的方式定义(a + b)的和。现在用反证法来证明"(a + b)不大于(C_{2})内的任何有理数"：假设(C_{2})内存在有理数(c_{0})以至于(a + b > c_{0})，那么根据上面证明过的"任何两个不相等的实数间存在无数个有理数"这点可知在0和(a + b - c_{0})之间存在有理数(q)，即(a + b - c_{0} > q > 0)，进一步可得到(left( a - frac{q}{2} ight) + (b - frac{q}{2}) > c_{0})，因为(a)是(A_{1})的最小上界，(b)是(B_{1})的最小上界，那么在(A_{1})和(B_{1})内必然分别存在有理数(a_{0})和(b_{0})满足({a > a}_{0} > left( a - frac{q}{2} ight))和({b > b}_{0} > (b - frac{q}{2}))，进而有(a + b{> a_{0} + b}_{0} > left( a - frac{q}{2} ight) + (b - frac{q}{2}) > c_{0})，从中竟然得出(C_{2})内的数(c_{0})小于(C_{1})内的数({a_{0} + b}_{0})，这与分割(C_{1}|C_{2})的定义相悖，所以(a + b)不大于(C_{2})内的任何有理数，因此(a + b)是产生分割(C_{1}|C_{2})的数，就有(a + b = c)。通过构造分割(C_{1}|C_{2})的方式，一方面我们定义了(a + b)的和，另外还可以通过c与(C_{1})和(C_{2})内的有理数大小关系来感知c的大小——c是不小于(C_{1})内的每个有理数同时也不大于(C_{2})内的每个有理数的唯一实数。应用类似的方法还可以定义实数(a)和(b)的乘法并且最终证明有理数的运算法则和运算性质（特指如下几条）同样适用于实数。

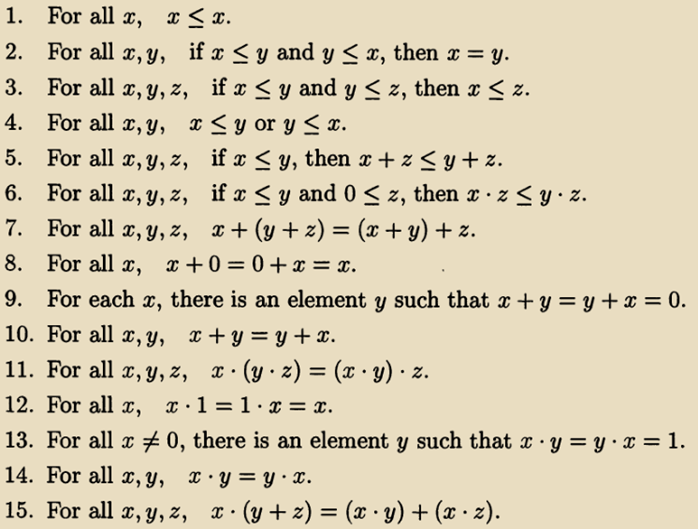
希望深入了解的读者可以去看David French Belding和Kevin J. Mitchell的Foundations of Analysis, 2nd Edition,可从19页看起，或D.C. Goldrei的 Classic Set Theory: For Guided Independent Study，从第二章看起，阅读时要注意本文与这些书所不同的是并没有把实数看作是有理数集的分割。

没有有理数来产生(A_{1} = { x in mathbb{Q}|x^{2} < 2mathrm{ }mathrm{ ext{or}}mathrm{ }x < 0})和(A_{2} = { x in mathbb{Q}|x^{2} > 2mathrm{ }mathrm{ ext{and}}mathrm{ }x > 0})组成的分割(A_{1}|A_{2})，但有唯一的实数c可以产生这个分割，那么(c^{2} = 2)吗？一个实数的平方只有小于或等于或大于2三种情况，如果能证明(mathbf{c}^{mathbf{2}}mathbf{< 2})和(mathbf{c}^{mathbf{2}}mathbf{>}mathbf{2})都会引出矛盾，那么(c^{2})必然等于2。这里c显然是个正数，为了简化问题，我们就在正数范围内讨论本问题。如何引出矛盾呢？假设(c^{2} < 2)时，如果能证明存在有理数(mathbf{q})使得(mathbf{c}^{mathbf{2}}mathbf{<}mathbf{q}^{mathbf{2}}mathbf{< 2})，这就会造成(A_{1})内的有理数q大于(A_{1})的最小上界c这种矛盾，那么如何证明存在这样的有理数(q)呢？如果有办法可以证明存在着比c还大的实数d满足(mathbf{c}^{mathbf{2}}mathbf{<}mathbf{d}^{mathbf{2}}mathbf{< 2})，那么通过"任何两个不相等的实数间存在无数个有理数"这条结论就可以知道存在有理数(q)满足(c < q < d)，再根据"如果(0 < q < d)，那么(q^{2} < d^{2})"这个不等性质可知(q^{2} < 2)，可见，问题最终可归结到满足条件的实数d是否存在。首先因为(c^{2} < 2)，只要选定足够大的正整数(n)就可以让(c + frac{1}{n})变得比(c)稍大一点点，那么我们很自然就会想：是不是存在正整数(n)使得实数(d = c + frac{1}{n})以至于({d^{2} = left( c + frac{1}{n} ight)}^{2} < 2)呢？因为(d^{2} = left( c + frac{1}{n} ight)^{2} = c^{2} + frac{2c}{n} + frac{1}{n^{2}} < c^{2} + frac{2c}{n} + frac{1}{n} = c^{2} + frac{1}{n}(2c + 1))，如果能证明存在正整数(n)使得(c^{2} + frac{1}{n}(2c + 1) < 2)，那么(d^{2} < 2)自然得证。对(c^{2} + frac{1}{n}(2c + 1) < 2)稍作变形可得(frac{1}{n} < frac{2 - c^{2}}{2c + 1}) ，现在问题变成了是否存在正整数(mathbf{n})使得(frac{mathbf{1}}{mathbf{n}}mathbf{<}frac{mathbf{2 -}mathbf{c}^{mathbf{2}}}{mathbf{2}mathbf{c + 1}}) ，因为(c)是正数且(c^{2} < 2)，所以(frac{2 - c^{2}}{2c + 1})是正数，根据"对于任意正实数(x)，总存在正整数(n)使得(frac{1}{n} < x)"得知存在这样的正整数(n)，也就存在正整数(n)使得实数(d = c + frac{1}{n})以至于({d^{2} = left( c + frac{1}{n} ight)}^{2} < 2)，而d的存在，根据前面的分析知道是对假设(c^{2} < 2)会产生矛盾的有力证据，用同样的方法也可以证明(c^{2} > 2)时也会产生矛盾，所以(A_{1} = { x in mathbb{Q}|x^{2} < 2mathrm{ }mathrm{ ext{or}}mathrm{ }x < 0})和(A_{2} = { x in mathbb{Q}|x^{2} > 2mathrm{ }mathrm{ ext{and}}mathrm{ }x > 0})组成的分割(A_{1}|A_{2})是由正实数c产生的并且(c^{2} = 2)，可把c记为(sqrt{2})，从这里可以看到(sqrt{2})确实存在我们定义出的实数集里。

以有理数集为基础通过简单易懂的方式构建一个数的连续体（实数集），并让读者明白几条实数的关键性质，这就是本文的主要使命。【完】

---

1. Courant and Robbins, What Is Mathematics? Second Edition, P60 ↩︎

2. John Stillwell, Numbers and Geometry, P260 ↩︎

3. Richard Dedekind, Essays on the Theory of Numbers, P5 ↩︎

4. Richard Dedekind, Essays on the Theory of Numbers, P5 ↩︎

5. Richard Dedekind, Essays on the Theory of Numbers, P9 ↩︎

6. Richard Courant, Fritz John, Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, P2 ↩︎

7. Terence Tao, Analysis I, third edition, P117 ↩︎

8. David French Belding, Kevin J. Mitchell, Foundations of Analysis, 2nd Edition, P21 ↩︎

9. David French Belding, Kevin J. Mitchell, Foundations of Analysis, 2nd Edition, P21 ↩︎

10. Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P984 ↩︎

11. Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P986 ↩︎

12. D.C. Goldrei， Classic Set Theory: For Guided Independent Study，P8 ↩︎

13. Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P987 ↩︎

14. P. Ehrlich，Real Numbers, Generalizations of the Reals, and Theories of Continua， page x ↩︎

15. Hans Niels Jahnke ，A History of Analysis，P306 ↩︎

16. S. C. Malik， Principles of Real Analysis，P18 ↩︎

17. Courant and Robbins, What Is Mathematics? Second Edition, P71 ↩︎

18. Rudiments of Mathematics Part 1, Academic Publishers,P15 ↩︎

19. Richard Dedekind, Essays on the Theory of Numbers, P7 ↩︎

20. Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P986 ↩︎