极限,比如说数列极限,简单讲来说的是“当n越来越大时,数列({{ a}_{n}})越来越靠近实数L”,是一种动态过程,而其正式定义,也称为数列极限的(ε, N)定义,却这么描述:设 (left{ a_{n} ight}) 为数列,(a) 为定数,若对任给的正数 (varepsilon), 总存在正整数 (N),使得当(n > N)时有(left| a_{n} - a ight| < varepsilon),则称数列 (left{ a_{n} ight}) 收敛于(a),定数(a)称为数列 (left{ a_{n} ight})的极限1。初学者对极限的直观印象在这种定义里几乎完全得不到反映,好多学生看后不知所言为何物,然后却又不得不马上拿着这个定义去证明各种极限,即便是最后很机械地、按部就班地凑出了该定义要求的形式,学生们对这一切还是耿耿于怀,不知道自己在干什么,究其原因是因为这个定义不够直观、不容易从中看出极限的“影子”,更具体来讲,极限最初在我们的直观认识里是一个动态概念,如本文一开始所说的那样,它是一种动态过程,但在该定义里这种动态过程并没有得到体现,所以这个定义也被称为极限的静态(static)定义2,本文将提出一种更直观的数列极限的动态(dynamic)定义,然后阐明它和静态定义的关系,并提出几条教学建议。
下文将先用苏格拉底教学法(Socratic method)行文,旨在通过启发性的方式一步一步地构建出严谨的数列极限动态定义。
师:当n越来越大时,数列({{ a}_{n}})越来越靠近极限值L。这一现象用数学语言怎么描述?
生:对于数列中任意一项(a_{p})及其后面任意一项(a_{q})有({|a}_{p} - L| > {|a}_{q} - L|)。如果我们拿这个条件来以(a_{q})作为起点的话,那么其后必有任意一项(a_{r}满足{|a}_{q} - L| > {|a}_{r} - L|),这样如果先记(a_{p}),(a_{q}),(a_{r})三项的下标p,q,r分别为(n_{1}, n_{2},n_{3}),用同样的方法后续我们还可以找到(n_{4}, n_{5},n_{6},ldots)以至于有
[{|a}_{n_{1}} - Lleft| > {|a}_{n_{2}} - L ight| > {|a}_{n_{3}} - L| > ldots]
这实际上是上面的约束条件的另外一种等价表述,该不等式表达了“后面的项总比前面的项更靠近极限”这个意思。
师:如果要让你的描述对常数数列的极限情况仍然适用,该怎么修改?
生:那应该改成(geq),即:对于数列中任意一项(a_{p})及其后面任意一项(a_{q})有({|a}_{p} - L| geq {|a}_{q} - L|)。
师:现在让我们来看(y = frac{sin x}{x}),当x越来越大时,也即分母越来越大时,由于分子sinx始终在-1到1之间,所以函数值在x越来越大时越来越靠近0。
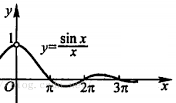
现在我们构造一数列({{ a}_{n}}),每个(a_{n})的值均是((n-1)π, nπ)上函数值域中的任意一个,那么该数列有极限吗?如果有,极限是多少?
生:有极限,值为0。因为函数值在x越来越大时整体越来越靠近0,从各区间((n-1)π, nπ)上函数值域中任意取出来的值组成的数列也符合这一趋势,所以数列({{ a}_{n}})的极限也是0。
师:很好!那对于该数列的极限你之前的数学语言还适用吗?
生:我发现这种情形下可能会有({|a}_{p}| < |a_{q}|)的情况,而这里L=0,所以就不会有({|a}_{p} - L| geq {|a}_{q} - L|)这个结果了,所以只有把“任意的(a_{q})”改成“存在(a_{q})”才行,即:对于数列中任意一项(a_{p}),其后总存在(a_{q})使得({|a}_{p} - L| geq {|a}_{q} - L|)。
师:对,在极限过程中并非后面的项都比前面的项更靠近极限,而是存在后面的项比前面的项更靠近极限,这个例子加深了我们对极限现象的准确掌握。
生:是的,确实有了进一步的认识。
师:如果将数列({frac{1}{n}})的前10000项都换为0,那么这个数列的极限还是不是0的?
生:呃……也是,毕竟极限研究更关心的是数列足够靠后的所有项的表现,前面有限多项的值是什么我们并不关心。
师:好,认识到这点之后你刚才的数学语言仍能描述这种情况吗?
生:不能了,如果(a_{p} = a_{10000} = 0),那么(a_{p})的后面就找不到(a_{q})使得({|a}_{p} - L| geq {|a}_{q} - L|)了。所以不能说(a_{p})也是可以任意取的了,(a_{p})的选取要看数列中是否存在有限个(正整数个)值为极限值的项,如果存在,那么可以要求(a_{p})取数列中值为极限值的最后那一项之后的任意一项,否则的话(a_{p})可任取。所以我的表述可以修改为:对于数列中某项之后的任意(a_{p})(这里的“某项”要看数列中是否存在正整数个值为L的项来定),其后总存在(a_{q})使得({|a}_{p} - L| geq {|a}_{q} - L|)。这里因为(a_{p})的选取条件导致整个描述稍显啰嗦,不够简洁,所以可改成另外一种更简洁的表述:存在(a_{n_{1}}),(a_{n_{2}}),(a_{n_{3}}),…满足({|a}_{n_{1}} - L| geq {|a}_{n_{2}} - L| geq {|a}_{n_{3}} - L| geq ldots),其中(n_{1}, n_{2},n_{3},ldots)均是原数列中满足本不等式的任意一项的下标,并且(n_{1} < n_{2} < n_{3} < ldots)。
师:对于数列({frac{1}{n}}),当n越来越大时,(frac{1}{n})越来越靠近0,但(frac{1}{n})是不是也越来越靠近(- 1)呢?
生:呃……也是啊!
师:你现在的极限语言排除得了这种情况吗?
生:不能。
师:所以你现在的描述只反映出总有后面的项比前面的项更接近于L,没反映出数列({{ a}_{n}})足够靠后的所有项可以无限接近L,或者说没有限制足够靠后的所有项接近的只能是L而不是其它数。
生:是哦!那么我认为还必须要求自某一项之后的所有项和L的差值都小于预先任意指定的足够小的正数,这一要求用数学符号语言可以表述为:总有某项之后的所有(a_{n})满足({|a}_{n} - L| < varepsilon),这里ε是足够小的正实数。
师:ε取1可以吗?
生:呃……也可以,不过1不够小,换为0.1似乎会更好点。
师:那为什么0.1可以而1就不妥呢?你判断的标准是什么?
生:我只是凭感觉觉得1似乎不能当作足够小的正实数,0.1倒是可以。
师:数学理论是不能靠着这种模糊不清的凭感觉的方式提出的,你必须给“足够小的正实数”一个明确的定义才行。
生:不妨定义任何在( (0, frac{1}{10^{M}} brack)内的数都是“足够小的正实数”,其中(M)是预先任意指定的正整数,简单起见,我们甚至可以直接取ε为(frac{1}{10^{M}}),即(varepsilon = frac{1}{10^{M}})。这样前面这个条件就应该改成:总有某项之后的所有(a_{n})满足({|a}_{n} - L| < frac{1}{10^{M}}),这里M是预先任意指定的正整数。
师:哈,孺子可教也!
生:承蒙老师指点!
至此,我们就得出了能完全描述数列极限现象的两个条件:
总有后面的项比前面的项更接近于实数L,对应的数学语言描述是:存在(a_{n_{1}}),(a_{n_{2}}),(a_{n_{3}}),…满足({|a}_{n_{1}} - L| geq {|a}_{n_{2}} - L| geq {|a}_{n_{3}} - L| geq ldots),其中(n_{1}, n_{2},n_{3},ldots)均是原数列里满足本不等式的任意一项的下标,且(n_{1} < n_{2} < n_{3} < ldots)。
足够靠后的所有项可以接近实数L到任意程度,对应的数学语言描述是:总有某项之后的所有(a_{n})满足({|a}_{n} - L| < frac{1}{10^{M}}),此处M是预先任意指定的正整数,这里的“某项”只能通过解这个不等式来确定。
任何满足上述两个条件的实数L就称为数列({{ a}_{n}})的极限,极限的动态过程在条件(1)里得到了反映,所以我们可以把上述两个条件看作是数列极限的动态定义。
现在让我们回头再看最初对数列极限的感性认识:“当n越来越大时,数列({{ a}_{n}})越来越靠近极限值L”,这种认识反映的只是上述的条件(1)而疏漏了条件(2),由此可见这种直观认识的缺陷,作为修正,我们可以这么说:如果当n越来越大时,数列({{ a}_{n}})越来越靠近实数L,并且足够靠后的所有项可以接近实数L到任意程度,则称L是({{ a}_{n}})的极限。
再看极限的(ε, N)定义,该定义反映不出极限的动态性,它只表明对于任给的正数(varepsilon)总有某项之后的所有(a_{n})满足({|a}_{n} - L| < varepsilon),其次,为了说明数列里足够靠后的所有项可以接近极限值到任意程度,该定义用了任意指定的正数ε来限定二者间的差距,然而这是一种很松散的、模棱两可的限定,因为ε即可以往小了取也可以往大了取,自然就不能够明确反映出“数列里足够靠后的所有项可以接近极限值到任意程度”这层意思,所以在本文给出的极限动态定义中直接用(frac{1}{10^{M}})取代ε,因为对于(frac{1}{10^{n}}),当n越来越大时,(frac{1}{10^{n}})便会越来越小,越来越靠近0,变得要多小有多小,所以笔者相信用(frac{1}{10^{M}})取代ε能反映出数列里的项可以接近极限值到任意程度这层意思,请读者就此再次回顾条件(2)。
实际上有了条件(2)便自然有条件(1),证明:取满足({frac{1}{10^{M}} > |a}_{n} - L|)的一项为(a_{n_{1}}),如果数列中有正整数个值为L的项,那么可以要求(a_{n_{1}})取数列中值为L的最后那一项之后的任意一项,然后取满足(|a_{n_{1}} - L| geq {|a}_{n} - L|)的一项为(a_{n_{2}}),取满足(|a_{n_{2}} - L| geq {|a}_{n} - L|)的一项为(a_{n_{3}}),…其中(n_{1}, n_{2},n_{3},ldots)均是原数列里满足本不等式的任意一项的下标,并且(n_{1} < n_{2} < n_{3} < ldots),显然(a_{n_{1}}),(a_{n_{2}}),(a_{n_{3}}),…能满足条件(1)。所以从逻辑角度来看,条件(1)不是必要的,但如果把条件(1)去掉,那么极限的“动态性”便得不到反映了。实际上把条件(2)里的(frac{1}{10^{M}})换回ε便是我们既熟悉又陌生的数列极限的(ε, N)定义3,也就是说去掉条件(1)之后极限的动态定义就变成了静态定义,但静态定义相比于动态定义并不能很贴切地、很直观地反映极限现象。所以虽然从逻辑角度来看条件(1)是多余的,但从认知角度来看它的存在却是大有裨益的——它反映着极限的动态性,它使得极限定义更加符合我们的直观认识,没有了它的极限静态定义会在理解上给学生带来很大的困难。所以笔者提议:(1)以本文的动态定义作为数列极限的标准定义,因为它使得极限定义更加符合我们的直观认识,进而就可以避免静态定义给学生造成的那些理解上的困难;(2)以现在教材里的(ε, N)定义作为极限值的判定方法,因为它相比极限动态定义更简洁,用来判定极限自然就比动态定义更方便;(3)如果前两条建议都得不到采纳, 那么至少应该介绍一下如何从极限动态定义走向静态定义,否则的话当前不少学生受极限静态定义之苦的局面仍然得不到解决;(4)函数极限的(ε, δ)定义也同样给学生们带来了不符合直觉的困惑,可以考虑用海涅(Eduard Heine)的极限定义来作为函数极限的正式定义4(具体是:对于任何一个收敛于(x_{0})的数列({{ x}_{n}}),且各个(x_{n} eq x_{0}),如果数列({{ f(x}_{n})})的极限是L,那么我们说L是(f(x))在(x_{0})处的极限),因为该定义更能反映出函数极限的动态性。 (ε, δ)定义可用来作为判定极限值的方法。