三倍经验
题意
给出一个长度为n的数列A,每次可以任选一段区间[l,r],使A[l]到A[r]全部-1,最终将整个序列减到0,求最小操作次数.
分析
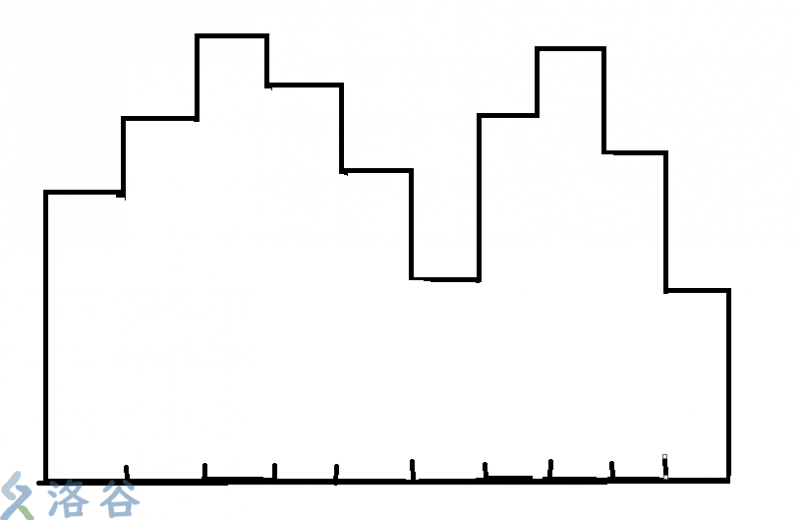
一开始的序列可以转化成这个样子.
每一次选取一段区间-1,可以怎么操作呢?
1.暴力枚举区间,然后暴力-1
emmm,时间复杂度:O(不能过),pass.
※期望得分:0;
2.线段树
emmmmmmm,勇气可嘉,但是还要动动脑子,不要一看到区间加减就开始上奇怪的数据结构.
3.O(n)递推
其实这是我在做NOIP2013/2018的T1时的做法.看图:
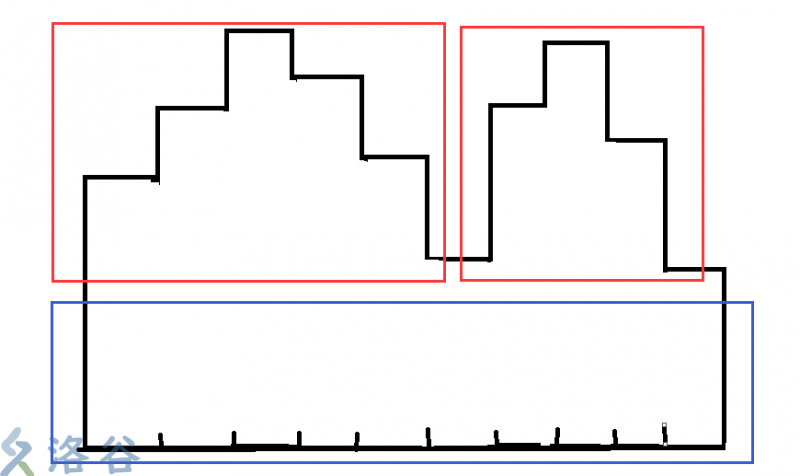
很容易可以看出,两个红色框部分是不能一起减掉的,只能两堆分开减,因为中间有一个低谷将两边的堆隔开,那么在最优情况下,这个低谷一定比两堆更早减为0,于是两堆注定隔开.但是下面蓝色框的部分就属于两堆的公共部分,只要在减其中一堆时顺便减掉它就好了.而且,加入我们把序列的第n+1位看成0的话,它就相当于一个一低到底的低谷,有了这些,我们就可以得出以下思路:
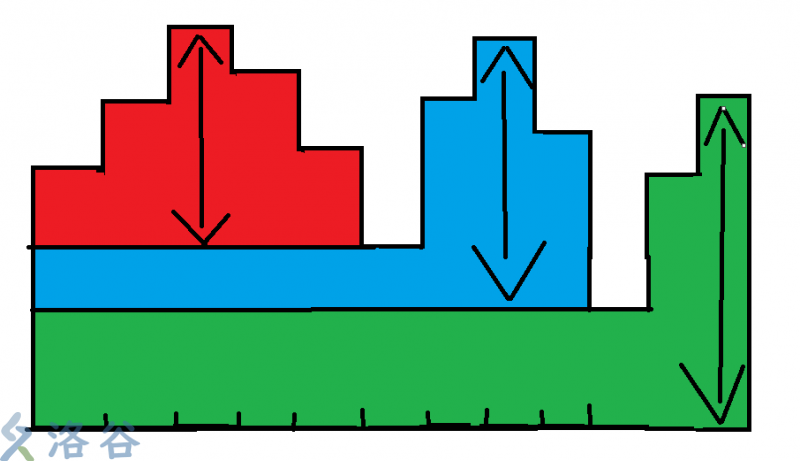
如图,每当我们遇到一个低谷,我们就将目前路过的这座山峰,也就是上一个峰顶-这一个谷底的高度减去,这样最后当遇到第n+1位的0时,一定能将剩下所有的高度减掉.这样就保证了只有被迫隔开的山峰是需要分别减去的,而公共部分的次数都没有浪费.不明白的话可以画图模拟一下.
核心代码:
long long h[N], ans//A序列,答案;
for (int i = 1; i <= n ; ++i) {
if (h[i] > h[i + 1]) {//当遇到峰顶时记录下现在的高度
long long temp = h[i];
while (h[i] > h[i + 1]) //一路找到谷底
i++;
ans += temp - h[i];记录答案
}
}
这样就可以解决了!
※期望得分:100
4.差分
差分是一个绝妙的思想,对A建立差分数组B,差分数组意味着B[i]=a[i]-a[i-1],也就是将A序列每一位和前一位的差记录下来.
如果要实现区间[l,r]-1,我们只需要B[l]-1,B[r+1]+1就可以了(想一想,为什么)
于是这个A序列就变成了B序列.要想让A序列归零,我们就要让B序列归零(想一想,是不是).显然,B中的每一个正数,后面都有负数与它对应,因此我们只需要将这个序列中所有的正数加起来,就是我们操作的总次数!
核心代码:
long long A[N], B[N], ans;
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> A[i];
B[i] = A[i] - A[i - 1];
if (B[i] > 0)
ans += B[i];
}
cout << ans << endl;
return 0;
}
※期望得分:100
最后还有一句话要提醒:
三年OI一场空,不开long long见祖宗
欢迎批评和指正!