0、对数器
在了解排序算法之前,引入对数器这一概念,它用于辅助验证自己写的排序算法正确与否。
使用步骤:
0,有一个你想要测的方法a
1,实现一个绝对正确但是复杂度不好的方法b
2,实现一个随机样本产生器
3,实现比对的方法
4,把方法a和方法b比对很多次来验证方法a是否正确
5,如果有一个样本使得比对出错,打印样本分析是哪个方法出错
6,当样本数量很多时比对测试依然正确,可以确定方法a已经正确

1 // 1,实现一个绝对正确但是复杂度不好的方法b 2 public static void comparator(int[] arr) { 3 Arrays.sort(arr); 4 } 5 6 // 2,实现一个随机样本产生器 7 public static int[] generateRandomArray(int maxSize, int maxValue) { 8 int[] arr = new int[(int) ((maxSize + 1) * Math.random())]; 9 for (int i = 0; i < arr.length; i++) { 10 arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random()); 11 } 12 return arr; 13 } 14 15 // for test 16 public static int[] copyArray(int[] arr) { 17 if (arr == null) { 18 return null; 19 } 20 int[] res = new int[arr.length]; 21 for (int i = 0; i < arr.length; i++) { 22 res[i] = arr[i]; 23 } 24 return res; 25 } 26 27 // 3,实现比对的方法 28 public static boolean isEqual(int[] arr1, int[] arr2) { 29 if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) { 30 return false; 31 } 32 if (arr1 == null && arr2 == null) { 33 return true; 34 } 35 if (arr1.length != arr2.length) { 36 return false; 37 } 38 for (int i = 0; i < arr1.length; i++) { 39 if (arr1[i] != arr2[i]) { 40 return false; 41 } 42 } 43 return true; 44 } 45 46 // for test 47 public static void printArray(int[] arr) { 48 if (arr == null) { 49 return; 50 } 51 for (int i = 0; i < arr.length; i++) { 52 System.out.print(arr[i] + " "); 53 } 54 System.out.println(); 55 } 56 57 // 4,把方法a和方法b比对很多次来验证方法a是否正确 58 public static void main(String[] args) { 59 int testTime = 500000; 60 int maxSize = 100; 61 int maxValue = 100; 62 boolean succeed = true; 63 for (int i = 0; i < testTime; i++) { 64 int[] arr1 = generateRandomArray(maxSize, maxValue); 65 int[] arr2 = copyArray(arr1); 66 // 0,有一个你想要测的方法a 67 bubbleSort(arr1); 68 comparator(arr2); 69 if (!isEqual(arr1, arr2)) { 70 succeed = false; 71 break; 72 } 73 } 74 System.out.println(succeed ? "True" : "False"); 75 // 5,如果有一个样本使得比对出错,打印样本分析是哪个方法出错 76 int[] arr = generateRandomArray(maxSize, maxValue); 77 printArray(arr); 78 bubbleSort(arr); 79 printArray(arr); 80 } 81 82 // 6,当样本数量很多时比对测试依然正确,可以确定方法a已经正确
1、冒泡排序(时间复杂度O(N^2),额外空间复杂度O(1))
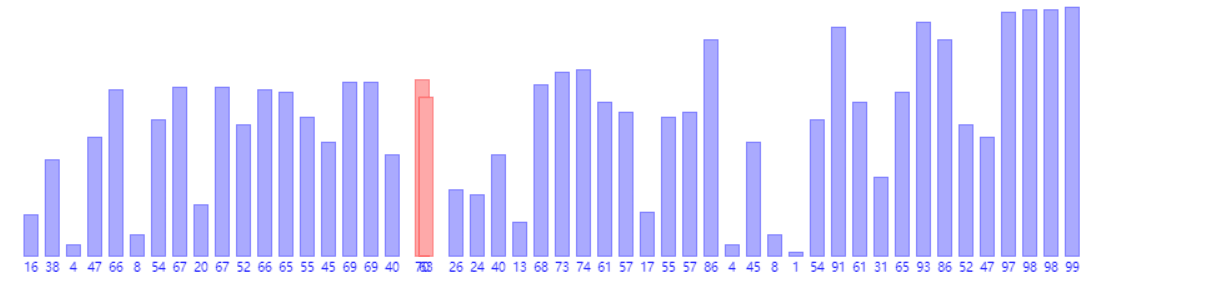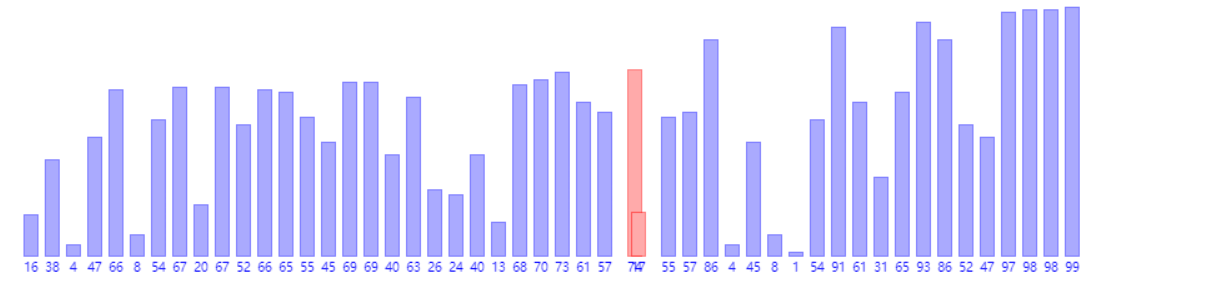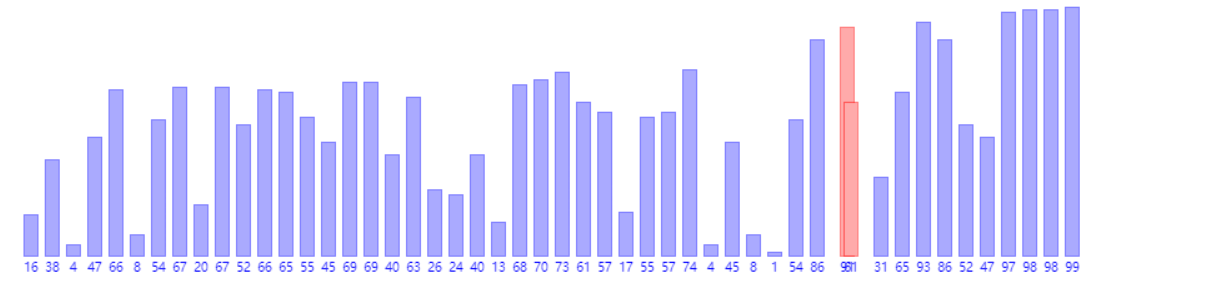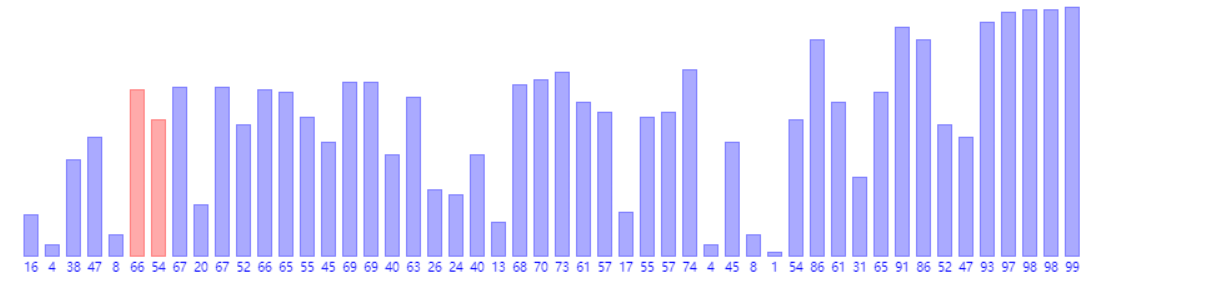
1 public static void bubbleSort(int[] arr) { 2 if (arr == null || arr.length < 2) { 3 return; 4 } 5 for (int i = arr.length - 1; i > 0; i--) { 6 for (int j = 0; j < i; j++) { 7 if (arr[j] > arr[j + 1]) { 8 swap(arr, j, j + 1); 9 } 10 } 11 } 12 } 13 14 public static void swap(int[] arr, int i, int j) { 15 arr[i] = arr[i] ^ arr[j]; 16 arr[j] = arr[i] ^ arr[j]; 17 arr[i] = arr[i] ^ arr[j]; 18 }
2.选择排序(时间复杂度O(N^2),额外空间复杂度O(1))
1 public static void selectionSort(int[] arr) { 2 if (arr == null || arr.length < 2) { 3 return; 4 } 5 for (int i = 0; i < arr.length - 1; i++) { 6 int minIndex = i; 7 for (int j = i + 1; j < arr.length; j++) { 8 minIndex = arr[j] < arr[minIndex] ? j : minIndex; 9 } 10 swap(arr, i, minIndex); 11 } 12 } 13 14 public static void swap(int[] arr, int i, int j) { 15 int tmp = arr[i]; 16 arr[i] = arr[j]; 17 arr[j] = tmp; 18 }
3.插入排序(时间复杂度O(N^2),额外空间复杂度O(1))

1 public static void insertionSort(int[] arr) { 2 if (arr == null || arr.length < 2) { 3 return; 4 } 5 for (int i = 1; i < arr.length; i++) { 6 for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) { 7 swap(arr, j, j + 1); 8 } 9 } 10 } 11 12 public static void swap(int[] arr, int i, int j) { 13 arr[i] = arr[i] ^ arr[j]; 14 arr[j] = arr[i] ^ arr[j]; 15 arr[i] = arr[i] ^ arr[j]; 16 }
4.归并排序(时间复杂度O(N*logN),额外空间复杂度O(N))
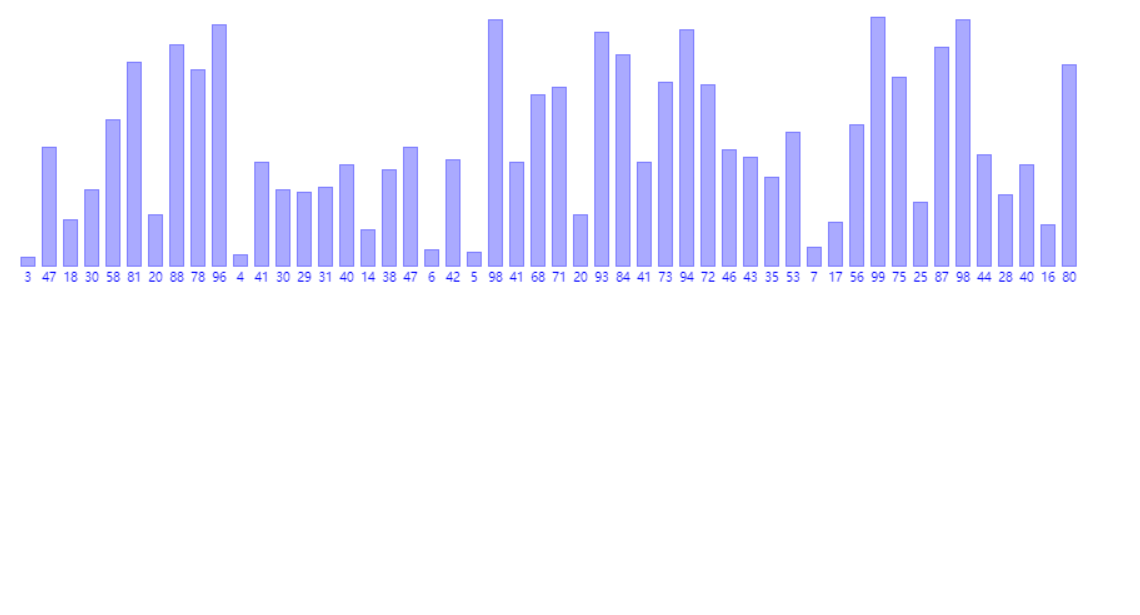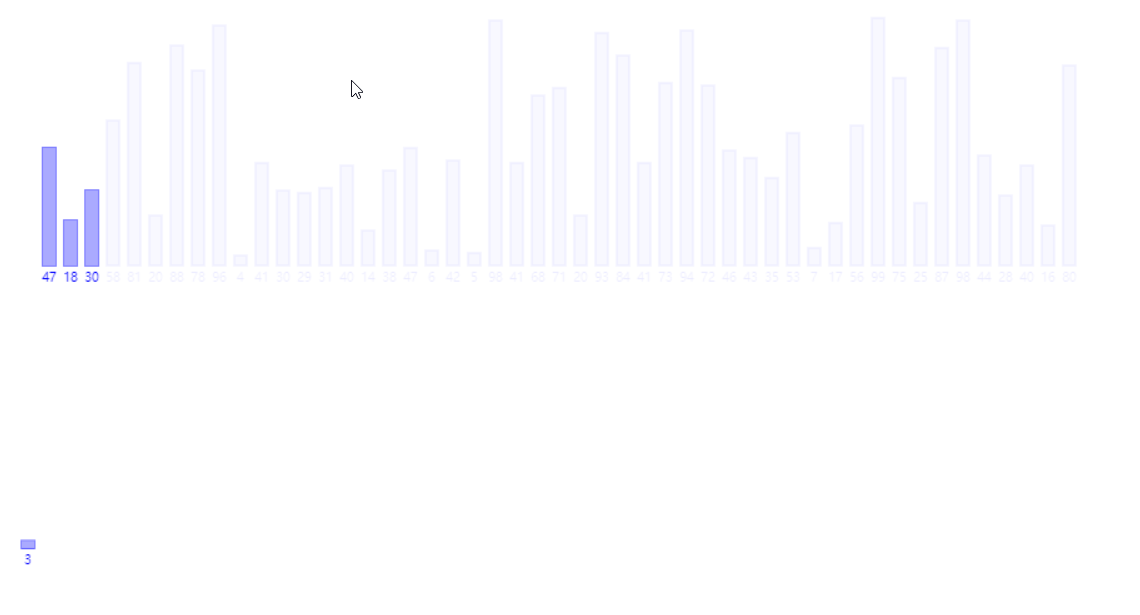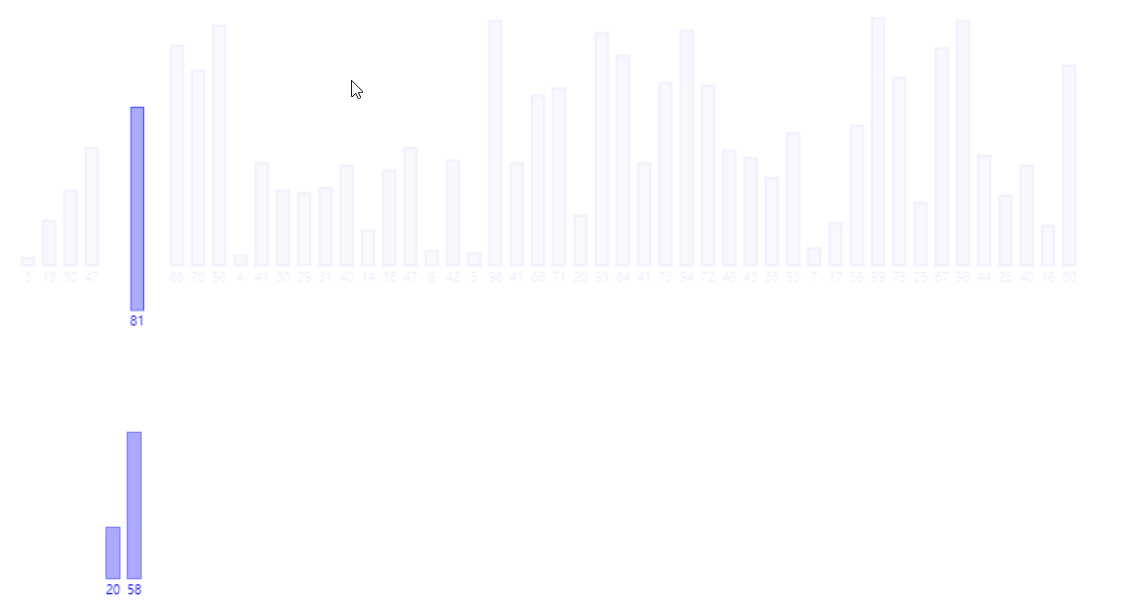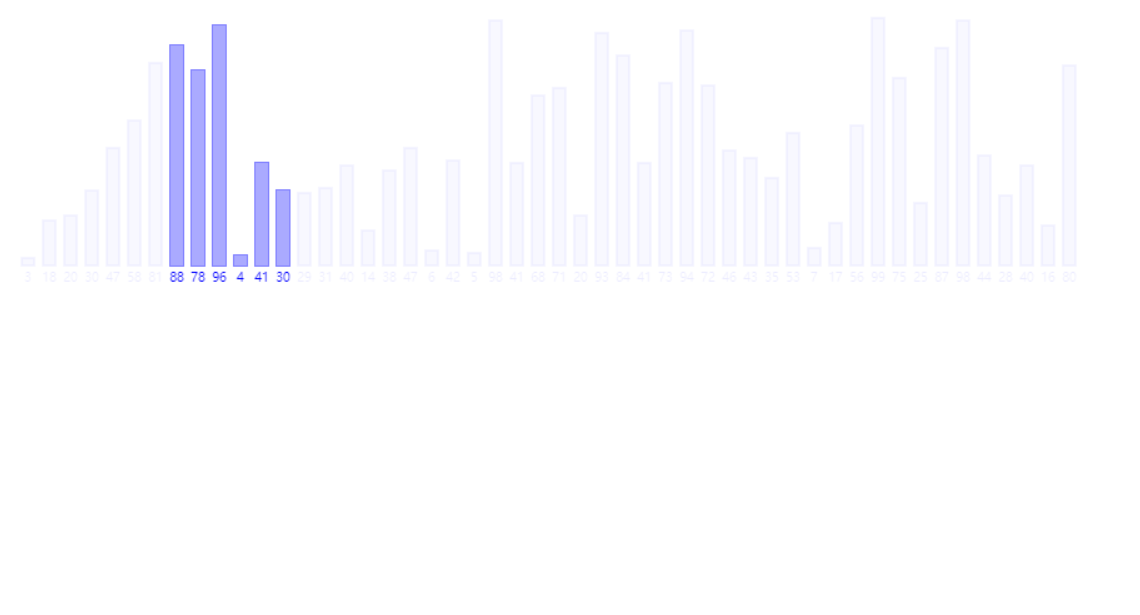
1 public static void mergeSort(int[] arr) { 2 if (arr == null || arr.length < 2) { 3 return; 4 } 5 mergeSort(arr, 0, arr.length - 1); 6 } 7 8 public static void mergeSort(int[] arr, int l, int r) { 9 if (l == r) { 10 return; 11 } 12 int mid = l + ((r - l) >> 1); 13 mergeSort(arr, l, mid); 14 mergeSort(arr, mid + 1, r); 15 merge(arr, l, mid, r); 16 } 17 18 public static void merge(int[] arr, int l, int m, int r) { 19 int[] help = new int[r - l + 1]; 20 int i = 0; 21 int p1 = l; 22 int p2 = m + 1; 23 while (p1 <= m && p2 <= r) { 24 help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++]; 25 } 26 while (p1 <= m) { 27 help[i++] = arr[p1++]; 28 } 29 while (p2 <= r) { 30 help[i++] = arr[p2++]; 31 } 32 for (i = 0; i < help.length; i++) { 33 arr[l + i] = help[i]; 34 } 35 }
归并排序牵扯到递归,递归的时间复杂度分析遵守master公式,即:
T(N) = a*T(N/b) + O(N^d)
1) log(b,a) > d -> 复杂度为O(N^log(b,a))
2) log(b,a) = d -> 复杂度为O(N^d * logN)
3) log(b,a) < d -> 复杂度为O(N^d)
