题目描述:
给定n个数X1-Xn,求下面式子的值(整数部分):
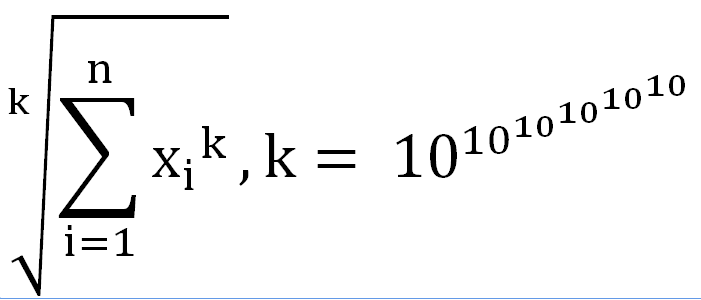
n<=107,xi<=109且互不相同。
分析:
其实一开始看见这道题我也吓傻了,k这么大,再说我又是数论鶸渣,打死也不会= =
后来看了各路神犇的题解,又仔细想了想,大概明白了。
首先,k这么大,已经不是高精乘和高精开方所能承受的了(当然,你也可以找个超级计算机算算试试)
所以我们可以把k视为∞(INF)。
极限思想,由于xi互不相同,所以每个元素在比它稍微大一点点的数面前都是微乎其微,不会影响到整数部分的。
(可以粗略验证,=101001e+100,9100=2.6561398887587476933878132203578e+95,差了5个数量级,在10100 面前9100可以忽略不计(毕竟只取整数嘛))
(或者直接算,100√10100 + 9100=10.00000265610496673245179467499,整数部分还是10)
也就是说,在k=INF的情况下,上述式子的整数部分即为
max{xi}
这么分析过后,题目就迎刃而解了。
贴出c++参考代码:(0.388 s,0.14 MB)
#include<cstdio>
int MAIN();
int n,temp=0,x=MAIN();
inline void read(int &x){//不用快读是上不了榜的
x=0;int c=getchar();
while(c<'0'||c>'9')c=getchar();
for(;c>='0'&&c<='9';c=getchar())x=(x<<1)+(x<<3)+(c^48);
return;
}
int main(){;}
inline int MAIN(){//减小常数,闲的没事者专用
freopen("math.in","r",stdin);
freopen("math.out","w",stdout);
read(n);
for(int i=0;i<n;i++){
read(x);
if(x>temp)temp=x;
}
return printf("%d",temp);
}