网络流不要算复杂度,远远达不到上界。但注意控制点数。
普通最大流可以处理无下界有上界的问题
最小割通常要找到性质转化为二分图。
双向边没必要建反向0流边
Dinic必要优化,rest=0 break,当前弧。
最大流
常见转化:
要求“至少”下界但没有上界,求“最小”。反一下。先满足所有要求,再最吝啬地拿走“最大流”。
例题
《士兵占领》:行列是独立的点集,在点放兵相当于在两个集间连边。反一下走流量就成了在该行该列同时减人,跑最大流即可。
拆点:很实用的思想,也很不好想。
如果$x1$在$Y$的操作对后面有影响,或$x$的顺序影响$Y$的贡献,且影响不能通过流量和费用表示出来,那么就可把$Y$拆成多个点,表示在某尺度上的差别。
例题
《紧急疏散evacuate》:一个人通过会在同一时间同一出口后卡住后面的人,而后面的人依旧可以被鸽到下一秒,所以把门拆成k个点,t向t+1连inf边。
《修车》:最小平均即求最小总时间,倒数第i个修有贡献i*t(让自己和后边的人都等了t),这个转化很妙。对于修的顺序有不同费用,所以对人和车的关系拆点(权值乘上倒数系数),跑最小费用最大流。
最小割
结论:最小割等于最大流
非板子,一般要找到二分图的性质。也就是说图不能太“长”。
常见模型:
多叉戟:选点有花费,点集有收益。(可以处理两种选择)
$|V|$和$|E|$都是m级别

inf边表示连通必不能割。
记总收益$sum=sumlimits_{i=1}^{m} w_i$。
割掉c代表为了保留(获得)w付出相应的代价,割掉w表示代价太高那不要收益。
综上用$ans=sum-maxflow$
例题:
《最大获利》:直接建三叉戟就行。
《happiness》:同时的关系要表现在同时割掉两个单边那么就要保留一个复合边,通过思考瞎试有下复合三叉戟结构
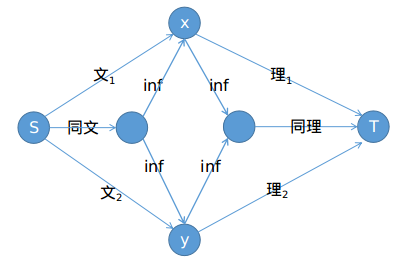
感觉没有什么规律,更多的是在试。。。
《employ人员雇佣》:咕
《切糕》:按纵轴建图,如果没有限制,答案就是最小割。现在考虑距离限制,inf边连两个纵轴,表示必须割一个,从而满足了下限,由于D一定,所以建出所有下限即可。有时间补图。
平面图转化对偶图
区域化点,对于原图中的边,从其分割的区域一边连向另一边,权值为原边的权值。
按照题意分出S和T区域,跑Dijkstra求出S到T的最短路径即是最小割。
特征:要求最小割,但范围大。网格或有规律,便于划分区域。
《狼抓兔子》
《海拔》:
性质:H的取值只可能是0或1,且所有0与左上联通,1与右下联通。
转化题意,求左上到右下的最小割。Dinic+当前弧 90 TLE
由于是有向边,要考虑割的方向,画图手模可出。或者无脑一点,统一顺时针或逆时针转90度,看隔开的是S->T还是T->S。
转化二分图
如果点对之间有关系,“配对”,强行把单点拆成X和Y部点,一方的改变会影响另一方,具有联动性。则可以考虑二分图。(不划成二分图一般极不可做)
接下来要找到转化二分图的标准:另同侧点集内部没有可改变的关系(一定满足或一定不满足),只存在X和Y之间的限制。
《数字配对》:分解质因数,则相差>=两个质数一定不能配对,按照素数个数分部,关系统一从X连向Y,S连X和Y连T限制数量。
《千钧一发》:大神结论。不能共存当且仅当满足
1.存在$c$满足$a_i^2+a_j^2=c^2$,$c$不一定是输入的
2.$gcd(a_i,a_j)==1$
有结论:奇数和奇数不满足1,偶数和偶数不满足2,所以按奇偶分部
证明:奇数平方%4=1,所以(奇数平方+奇数平方)%4=2,若$c$为奇数,$c^2$%4=1,不满足;若为偶数,$c^2$%4=0,不满足。综上奇数和奇数间没有直接限制。gcd的显然。
跑最小割,X和Y间连inf表示只能选一个。
费用流
SPFA找增广路,EK单路增广。
所以点数一般不超过500,边不超过20000。
ZKW费用流可以在权值范围很小的时候使用。
《晨跑》:模板题。拆点限制1流量。注意若x出和y入连inf,会在1->n有直接连边时inf次增广。
《修车》、《数字配对》都是费用流而重点不在这。
上下界网络流
1.可以解决一些dp不能做的覆盖问题。
2.无源汇看是否可以合并源汇而不影响答案(费用为0),或者全图流量平衡。
3.有源汇有上下界最小费用可行流,只要EK补流后的可行流就是最小费用可行流,不用再在原图上增广。
证明:已知T->S连inf流量0费用,若S->T能找到费用为负的增广路,则构成负环,与已有结论矛盾。证毕
进而推知无源汇有上下界最小费用可行流也是正确的。S和T相当于同一个点。
《支线剧情》:给定DAG,边有权值,最小花费用线段覆盖所有边。每个点向1连(inf,0)边。然后就是无源汇有上下界最小费用可行流。
《志愿者招募》:用有代价的不同且无限区间覆盖线性的点,每个点至少被覆盖给定次数$a_i$。这个模型在之前也有过,由于一些特殊性质往往可以贪心或dp。网络流可以给出$n<=1000 m<=10000(区间种数)$左右的通解。
点化边,那么边有流量限制$[a_i,inf]$,对于每种区间[l,r]从r的出连l的入$(inf,c_j)$。最后的合法情况就是原图流量平衡。这样我们为了达到流量平衡,不得不花费一定代价走区间的反边,spfa跑出最小增广路保证最优。为无源汇有上下界最小费用可行流。
《旅行时的困惑》:首先转化题意,把边反向,那么要求每条边至少被覆盖一次。比较明显的优化,超源汇只向出度或入度为零的点连边。由于正解不是网络流,要加当前弧卡过。
《清理雪道》:建图好说。不同在于要求最小流。从T->S跑Dinic找到满足的最大退流,减去即可。为有源汇有上下界最小流。
《矩阵》:好题。答案有单调性,考虑二分。按行列成二分图。对于ans,一定存在某行或某列$left |sumlimits A-sumlimits B ight |=mid$,独立出未知B,得出上下界为$[max(sum_i-x,nL),min(sum_i+x,nR)]$,列同理,S向行连,列向T连。行和列间连$[L,R]$,意义在于调整流量。check是否存在可行流。
最大权闭合子图
做法:S向正点权连边,负点权向T连边,记$sum=sumlimits 正点权$,那么最大权闭合子图的解为$sum-mincut$,子图为S所在的点集。
这里不再证明。主要记录下特征 思路。
特征(可以处理):
1.有先后限制关系。拿A才能拿B。(PVZ)
2.有包含关系。[l,r]包含[l+1,r] [l,r-1]。本质还是1。(寿司餐厅)
3.“归类”,对于集合S,若S的非空子集存在与闭合子图中,则集合S对应的点同必须存在闭合子图中。(寿司餐厅,代号)
例题:
《植物大战僵尸》:有先后限制,但不能直接建图。若出环,由题则一个也取不到,而一下拿走整个环在闭合子图中是合法的。所以先拓扑排序判掉环,然后根据先后限制建图求解即可。
《寿司餐厅》:由于$d_{i,j}$只会贡献一次,且多次取的寿司之间没有拼接,求一次最大权闭合子图是可行的。
隐藏的先后限制:
1.若拿$d_{i,j}$,则必须先取$d_{i+1,j} d_{i,j-1}$
2.若拿代号为i的寿司,则必须选代表i代号的点付出相应代价。“归类”
对于cx的代价,直接算在$d_{i,i}$中,拿几个就扣几个。