[补档]Password

Password

题目

Rivest是密码学专家。近日他正在研究一种数列E = {E[1],E[2],……,E[n]}，且E[1] = E[2] = p（p为一个质数），E[i] = E[i-2]×E[i-1] （若2<i<=n）。

例如{2,2,4,8,32,256,8192,……}就是p = 2的数列。在此基础上他又设计了一种加密算法，该算法可以通过一个密钥q (q < p)将一个正整数n加密成另外一个正整数d，计算公式为：d = E[n] mod q。现在Rivest想对一组数据进行加密，但他对程序设计不太感兴趣，请你帮助他设计一个数据加密程序。

INPUT

第一行读入m，p。其中m表示数据个数，p用来生成数列E。 以下有m行，每行有2个整数n，q。n为待加密数据，q为密钥。 数据范围: 0 < p n< 2^31 0 < q < p 0 < m <= 5000。

OUTPUT

将加密后的数据按顺序输出到文件 第i行输出第i个加密后的数据。

SAMPLE

INPUT1

2 7

4 5

4 6

OUTPUT1

3

1

INPUT2

4 7

2 4

7 1

6 5

9 3

OUTPUT2

3

0

1

1

解题报告

考试时候本以为推了个正解，又强行推出了实现，结果= =

还不如打个暴力

正解：

首先写个公式：

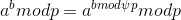
其中，phi(p)为p的欧拉函数。

不要问我怎么证，我不会

然后，我们可以得出，要求的显然就是p^fib(i)%q,其中fib(i)为斐波那契数列的第i项。

显然，正经递推斐波那契是会T的。所以我们考虑优化，显然可以用矩阵快速幂解决问题。

那么，剩下的就很简单了。直接快速幂就可以解决了。

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long L;
inline int read(){
    int sum(0);
    char ch(getchar());
    for(;ch<'0'||ch>'9';ch=getchar());
    for(;ch>='0'&&ch<='9';sum=sum*10+(ch^48),ch=getchar());
    return sum;
}
L m,p,n,q;
L fib;
L unit[2][2],start[2][2];
inline void multi(L a[][2],L b[][2],L mod){
    L tmp[2][2]={0};
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
            for(int k=0;k<2;k++)
                tmp[i][j]=(tmp[i][j]+a[i][k]*b[k][j])%mod;
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
            b[i][j]=tmp[i][j];
}
inline int get_phi(L x){
    L ret(x);
    for(int i=2;i*i<=x;i++)
        if(x%i==0){
            ret=ret-ret/i;
            while(x%i==0)
                x/=i;
        }
    if(x>1)
        ret=ret-ret/x;
    return ret;
}
inline L fi(L p,L mod){
/*  if(p==0)
        return 0;
    if(p==1||p==2)
        return 1;*/
    start[0][0]=start[1][0]=start[0][1]=1,start[1][1]=0;
    unit[0][0]=unit[1][1]=1,unit[1][0]=unit[0][1]=0;
    while(p){
        if(p&1)
            multi(start,unit,mod);
        multi(start,start,mod);
        p>>=1;
    }
    return unit[0][1];
}
L mod;
inline L qpow(L a,L p,L mod){
    L ret(1);
    while(p){
        if(p&1)
            ret*=a,ret%=mod;
        a*=a,a%=mod;
        p>>=1;
    }
    return ret;
}
int main(){
//  freopen("1.in","r",stdin);
//  freopen("1.out","w",stdout);
    m=read(),p=read();
    while(m--){
        n=read(),q=read();
        mod=get_phi(q);
        fib=fi(n,mod);
        fib%=mod;
        printf("%lld
",qpow(p,fib,q)%q);
    }
}