看题目就知道这是一个悲伤的故事。。。
但还有更悲伤的

考崩了,难以描述。
T1把数据范围看成2^12,我TM也是够了。。。
T2思路接近正解,但不知道想了个神魔东西跑了N遍dijstra
T3最狗了,暴力二十分没拿到,因为我打的贪心。。
T1:很水的DP+组合数学
DP转移显然:f[i][j]=sum[i-1][j-1]-sum[i-1][j-m];但是这样时空复杂度都是(N*d)但期望复杂度是(N^2)考虑如何优化发现f[i][j]实际上有许多零出现,但我们还把它当成有用的状态转移了,因此考虑抹去这些冗余。用组合数学,f[i][j]的定义改为送出礼物的i天 注意取模!
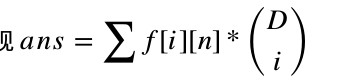
AC代码:

1 #include<bits/stdc++.h>
2 #define MAXN 2005
3 #define mem(a) memset(a,0,sizeof(a))
4 using namespace std;
5 const long long mod=998244353;
6 long long C[MAXN],inv[MAXN];
7 inline long long Rd()
8 {
9 long long x=0;char c=getchar();long long f=1;
10 while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
11 while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
12 return x*f;
13 }
14 long long n,d,m;
15 long long f[MAXN][MAXN],sum[MAXN][MAXN];
16 inline long long qpower(long long a,long long b)
17 {
18 long long ans=1;
19 while(b)
20 {
21 if(b&1)ans=ans*a%mod;
22 a=a*a%mod;
23 b>>=1;
24 }
25 return ans%mod;
26 }
27 inline void Get_C()
28 {
29 C[1]=d%mod;
30 for(long long i=2;i<=n;i++)
31 {
32 C[i]=C[i-1]*inv[i]%mod*((d-i+1)%mod)%mod;
33 }
34 }
35 int main()
36 {
37 //freopen("out.in","r",stdin);
38 //freopen("a.txt","w",stdout);
39 for(long long i=1;i<=2000;i++)inv[i]=qpower(i,mod-2);
40 while(1)
41 {
42 mem(sum);mem(f);
43 n=Rd();d=Rd();m=Rd();
44 long long ans=0;
45 Get_C();
46 if(n==0&&d==0&&m==0)return 0;
47 for(long long i=1;i<m;i++)f[1][i]=1,sum[1][i]=sum[1][i-1]+f[1][i];
48 for(long long i=m;i<=n;i++)sum[1][i]=sum[1][m-1];
49 for(long long i=2;i<=n;i++)
50 {
51 for(long long j=0;j<=n;j++)
52 {
53 if(j>=m)f[i][j]=(mod+sum[i-1][j-1]-sum[i-1][j-m])%mod;
54 else f[i][j]=sum[i-1][j-1];
55 sum[i][j]=(sum[i][j-1]+f[i][j])%mod;
56 }
57 }
58 for(int i=1;i<=n;i++)ans=(ans+C[i]*f[i][n]%mod)%mod;
59 cout<<ans%mod<<endl;
60 }
61 return 0;
62 }
T2:找最小环
想了一个**算法,时间复杂度O(n^2log(n))空间复杂度(n^2)

1 #include<cstdio>
2 #include<queue>
3 #include<bits/stdc++.h>
4 #define ts puts("---------------");
5 #define MAXN 20005
6 #define mem(a) memset(a,0,sizeof(a))
7 using namespace std;
8 int head[MAXN],nxt[MAXN],to[MAXN],cnt,s[MAXN],top,dfn[MAXN],low[MAXN],ans,tot,v[MAXN],val[MAXN];
9 bool yes_get,vst[1005],in_s[MAXN],Fail[MAXN*10];
10 int edge[2005][2005],d[1005],di[1005],pre[1005];
11 void clear()
12 {
13 mem(head);mem(s);mem(dfn);mem(in_s);mem(v);mem(Fail);mem(vst);mem(pre);
14 yes_get=ans=tot=cnt=top=0;
15 }
16 inline int Rd()
17 {
18 int x=0;char c=getchar();int f=1;
19 while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
20 while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
21 return x*f;
22 }
23 void add(int u,int v,int w)
24 {
25 to[++cnt]=v;
26 nxt[cnt]=head[u];
27 val[cnt]=w;
28 head[u]=cnt;
29 return ;
30 }
31 void Tarjan(int x,int fa)
32 {
33 dfn[x]=low[x]=++tot;
34 s[++top]=x;
35 in_s[x]=1;
36 for(int i=head[x];i;i=nxt[i])
37 {
38 int y=to[i];
39 if(y==fa)continue;
40 if(!dfn[y])
41 {
42 v[y]=val[i];
43 Tarjan(y,x);
44 low[x]=min(low[x],low[y]);
45 }
46 else
47 {
48 if(in_s[y])
49 {
50 if(dfn[y]<low[x])v[x]+=val[i];
51 low[x]=min(low[x],dfn[y]);
52 }
53 }
54 }
55
56 if(low[x]==dfn[x])
57 {
58 ans=0;
59 while(top)
60 {
61 int p=s[top--];
62 in_s[p]=0;
63 ans+=v[p];
64 if(p==1)yes_get=1;
65 if(p==x)break;
66 }
67 }
68 if(!yes_get||!ans)ans=-1;
69 else return ;
70 }
71 int Getmin(int i)
72 {
73 priority_queue<pair<int,int> >Q;
74 while(Q.size())Q.pop();
75 memset(di,0x3f,sizeof(di));
76 mem(vst);
77 di[1]=0;
78 Q.push(make_pair(0,1));
79 while(!Q.empty())
80 {
81 pair<int,int>k=Q.top();Q.pop();
82 int x=k.second;
83 if(vst[x])continue;
84 if(x==i)return di[x];
85 vst[x]=1;
86 for(int i=head[x];i;i=nxt[i])
87 {
88 if(Fail[i])continue;
89 int y=to[i],va=val[i];
90 if(va+di[x]<di[y])
91 {
92 di[y]=va+di[x];
93 Q.push(make_pair(-di[y],y));
94 }
95 }
96 }
97 return di[0];
98 }
99 void pre_Get()
100 {
101 priority_queue<pair<int,int> >Q;
102 memset(d,0x3f,sizeof(d));
103 mem(vst);
104 d[1]=0;
105 Q.push(make_pair(0,1));
106 while(!Q.empty())
107 {
108 pair<int,int>k=Q.top();Q.pop();
109 int x=k.second;
110 if(vst[x])continue;
111 vst[x]=1;
112 for(int i=head[x];i;i=nxt[i])
113 {
114 int y=to[i],va=val[i];
115 if(va+d[x]<d[y])
116 {
117 pre[y]=x;
118 d[y]=va+d[x];
119 Q.push(make_pair(-d[y],y));
120 }
121 }
122 }
123 return ;
124 }
125 int main()
126 {
127 // freopen("out.in","r",stdin);
128 // freopen("b.txt","w",stdout);
129 int t=Rd();
130 while(t--)
131 {
132 clear();
133 int n=Rd(),m=Rd();
134 if(n==m)
135 {
136 while(m--)
137 {
138 int u=Rd(),v=Rd(),w=Rd();
139 add(u,v,w);
140 add(v,u,w);
141 }
142 Tarjan(1,0);
143 cout<<ans<<endl;
144 }
145 else
146 {
147 ans=0x7f7f7f7f;
148 while(m--)
149 {
150 int u=Rd(),v=Rd(),w=Rd();
151 add(u,v,w);
152 edge[u][v]=cnt;
153 add(v,u,w);
154 edge[v][u]=cnt;
155 }
156 pre_Get();
157 for(int i=2;i<=n;i++)
158 {
159 if(d[i]==d[0])continue;
160 int t=i;
161 while(t!=1&&t!=0)
162 {
163 Fail[edge[pre[t]][t]]=1;
164 Fail[edge[t][pre[t]]]=1;
165 t=pre[t];
166 }
167 if(Getmin(i)!=di[0])ans=min(ans,Getmin(i)+d[i]);
168 t=i;
169 while(t!=1)
170 {
171 Fail[edge[pre[t]][t]]=0;
172 Fail[edge[t][pre[t]]]=0;
173 t=pre[t];
174 }
175 }
176 cout<<(ans==0x7f7f7f7f?-1:ans)<<endl;
177 }
178 }
179 return 0;
180 }
181 /*
182 1
183 4 5
184 1 2 2
185 2 3 2
186 3 4 2
187 1 4 2
188 1 3 5
189 */
但实际上仔细想想发现,我的算法是有许多冗余的,只需要枚举和一直接相邻的边就够了。
因此。。。
AC代码

1 #include<cstdio>
2 #include<queue>
3 #include<bits/stdc++.h>
4 #define ts puts("---------------");
5 #define MAXN 80005
6 #define mem(a) memset(a,0,sizeof(a))
7 using namespace std;
8 int head[MAXN],nxt[MAXN],to[MAXN],cnt=1,ans,val[MAXN];
9 bool Fail[MAXN],vst[10005];
10 int di[10005];
11 void clear()
12 {
13 mem(head);mem(Fail);
14 cnt=1;
15 }
16 inline int Rd()
17 {
18 int x=0;char c=getchar();int f=1;
19 while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
20 while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
21 return x*f;
22 }
23 void add(int u,int v,int w)
24 {
25 to[++cnt]=v;
26 nxt[cnt]=head[u];
27 val[cnt]=w;
28 head[u]=cnt;
29 return ;
30 }
31 int Getmin(int i,int ww)
32 {
33 priority_queue<pair<int,int> >Q;
34 while(Q.size())Q.pop();
35 memset(di,0x3f,sizeof(di));
36 mem(vst);
37 di[1]=0;
38 Q.push(make_pair(0,1));
39 while(!Q.empty())
40 {
41 pair<int,int>k=Q.top();Q.pop();
42 int x=k.second;
43 if(di[x]+ww>ans)return di[x]+ww;
44 if(vst[x])continue;
45 if(x==i)return di[x]+ww;
46 vst[x]=1;
47 for(int i=head[x];i;i=nxt[i])
48 {
49 if(Fail[i])continue;
50 int y=to[i],va=val[i];
51 if(va+di[x]<di[y])
52 {
53 di[y]=va+di[x];
54 Q.push(make_pair(-di[y],y));
55 }
56 }
57 }
58 return di[0];
59 }
60 int main()
61 {
62 // freopen("out.in","r",stdin);
63 // freopen("b.txt","w",stdout);
64 int t=Rd();
65 while(t--)
66 {
67 clear();
68 int n=Rd(),m=Rd();
69 ans=0x3f3f3f3f;
70 while(m--)
71 {
72 int u=Rd(),v=Rd(),w=Rd();
73 add(u,v,w);
74 add(v,u,w);
75 }
76 for(int i=head[1];i;i=nxt[i])
77 {
78 int k=to[i];
79 Fail[i]=Fail[i^1]=1;
80 ans=min(ans,Getmin(k,val[i]));
81 Fail[i]=Fail[i^1]=0;
82 }
83 cout<<(ans==0x3f3f3f3f?-1:ans)<<endl;
84 }
85 return 0;
86 }
87 /*
88 1
89 4 5
90 1 2 2
91 2 3 2
92 3 4 2
93 1 4 2
94 1 3 5
95 */
LNC的A*算法(借鉴一下,无意侵权)

1 #include<iostream>
2 #include<cstring>
3 #include<cstdio>
4 #include<cstring>
5 #include<queue>
6 using namespace std;
7 const int maxn=1e4+5,maxm=4e4+5,INF=0x3f3f3f3f;
8 int T,n,m,x,y,z,dex,yes,tot=1,top,cld[maxn],yet[maxn],instack[maxn],stack[maxn],first[maxn];
9 struct road{
10 int u,t,w,nxt;
11 }eage[maxm<<1];
12 struct point1{
13 int id,dis;
14 bool friend operator < (const point1 a,const point1 b)
15 {
16 return a.dis>b.dis;
17 }
18 }dis[maxn];
19 struct point2{
20 int id,h;
21 bool friend operator < (const point2 a,const point2 b)
22 {
23 return dis[a.id].dis+a.h>dis[b.id].dis+b.h;
24 }
25 };
26 priority_queue<point1> q1;
27 priority_queue<point2> q2;
28 void add(int x,int y,int z)
29 {
30 eage[++tot].u=x;
31 eage[tot].t=y;
32 eage[tot].w=z;
33 eage[tot].nxt=first[x];
34 first[x]=tot;
35 }
36 void clear()
37 {
38 top=0;tot=1;
39 memset(first,0,sizeof(first));
40 memset(cld,0,sizeof(cld));
41 memset(yet,0,sizeof(yet));
42 memset(instack,0,sizeof(instack));
43 }
44 void dijk()
45 {
46 memset(yet,0,sizeof(yet));
47 for(int i=1;i<=n;i++) dis[i].id=i,dis[i].dis=INF;
48 dis[1].dis=0;
49 q1.push(dis[1]);
50 while(q1.empty()==0)
51 {
52 int x=q1.top().id;q1.pop();
53 if(yet[x]) continue;
54 yet[x]=1;
55 for(int i=first[x];i;i=eage[i].nxt)
56 if(dis[x].dis+eage[i].w<dis[eage[i].t].dis)
57 dis[eage[i].t].dis=dis[x].dis+eage[i].w,q1.push(dis[eage[i].t]);
58 }
59 memset(yet,0,sizeof(yet));
60 }
61 int work(int st)
62 {
63 while(q2.empty()==0) q2.pop();
64 point2 x,tmp;
65 x.id=st;x.h=0;
66 q2.push(x);
67 int ans=INF;
68 while(q2.empty()==0)
69 {
70 x=q2.top();q2.pop();
71 yet[x.id]=1;
72 if(x.id==1)
73 {
74 ans=x.h;
75 break;
76 }
77 for(int i=first[x.id];i;i=eage[i].nxt)
78 if(i!=dex&&yet[eage[i].t]==0)
79 {
80 tmp.id=eage[i].t;
81 tmp.h=eage[i].w+x.h;
82 q2.push(tmp);
83 }
84 }
85 memset(yet,0,sizeof(yet));
86 return ans;
87 }
88 void Astar()
89 {
90 dijk();
91 int ans=INF;
92 for(int i=first[1];i;i=eage[i].nxt)
93 {
94 dex=i^1;
95 int t=eage[i].t,d=work(t)+eage[i].w;
96 ans=min(d,ans);
97 }
98 printf("%d
",ans>10000000?-1:ans);
99 return ;
100 }
101 int main()
102 {
103 scanf("%d",&T);
104 while(T--)
105 {
106 scanf("%d%d",&n,&m);
107 while(m--)
108 {
109 scanf("%d%d%d",&x,&y,&z);
110 add(x,y,z);add(y,x,z);
111 }
112 Astar();
113 clear();
114 }
115 }
T3:又是一道足以把评测机卡崩的题 好题标记
毫无头绪?
是的 毫无头绪是真的毫无头绪,但根据数据范围可以推测复杂度应该接近O(n)(T=50,5000ms限制啧啧啧)
就此展开,感觉dp否了,递推。。。也不大可能,所以我们自然会想到搜索图论,(好吧我承认有点牵强,但说实话,O(n)的算法真的不多,这总不能单队维护吧QwQ)
然后就会有奇妙的发现:如果两两连边HiaHiaHia,没神魔卵用,就会发现其实操作只是把边反过来而已。而题目的目标就是每个点的入度<=1。
既然这样,那就继续探索。把这个图画出来,手玩小样例后发现图被分成了几个连通块,然后就可以分类讨论了:
1.m>n 显然是不对的,因为要保证每条边都指向一个点,每个点又要被不大于一条边指(这这这不可能)。
2.m=n 是棵基环树!!!!先考虑环,环可以顺时针也可以逆时针,所以分两种情况,再看以环为根的子树,不管环咋转,子树永远是外向的,所以一遍dfs即可
3.m<n 要保证图联通所以这一定是棵树,而且是棵外向树,快乐吗?可问题是根是不确定的。
下面引入新概念:
二次扫描和换根法:对于不定根的树状DP,暴力枚举是O(n^2),但我们可以先考虑一个点,再考虑用已知点更新未知点,即考虑换根的代价。
但只适用于不管换不换根,旧根与新根的共同子树状态不变。(纯属博猪个人理解,如有错误,多谢指正)
好啦,有了这个强大的方法,我们就可以成功AC了
AC 代码:

1 #include<bits/stdc++.h>
2 #define mem(a) memset(a,0,sizeof(a))
3 #define MAXN 200000
4 using namespace std;
5 const int mod=998244353;
6 struct node{
7 int head[MAXN],to[MAXN],nxt[MAXN],cnt,dfn[MAXN],now_minn,now_tot,v[MAXN];long long tot;
8 int use,sum,fa[MAXN],d[MAXN],f[MAXN];
9 long long ans,minn;
10 bool orz[MAXN],vst[MAXN],inlop[MAXN],vst1[MAXN],vst2[MAXN];
11 vector<int>lop;
12 void clear()
13 {
14 lop.clear();cnt=1;ans=1;minn=0;tot=0;mem(fa);mem(v);
15 mem(inlop);mem(vst);mem(vst1);mem(vst2);
16 mem(d);mem(f);
17 mem(dfn);
18 mem(head);
19 }
20 void add(int u,int v,int opt)
21 {
22 to[++cnt]=v;
23 nxt[cnt]=head[u];
24 head[u]=cnt;
25 orz[cnt]=opt;
26 return ;
27 }
28 inline int Rd()
29 {
30 int x=0;
31 char c=getchar();
32 int f=1;
33 while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
34 while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
35 return x*f;
36 }
37 bool Getlop(int x,int edge)
38 {
39 dfn[x]=++tot;
40 for(int i=head[x];i;i=nxt[i])
41 {
42 if(i==(edge^1))continue;
43 int y=to[i];
44 if(dfn[y])
45 {
46 if(sum==1){sum++;continue;}
47 if(sum>1)return 0;
48 sum++;
49 inlop[y]=1;
50 lop.push_back(y);
51 if(orz[i])use=1;
52 else use=0;
53 int p=x;
54 while(p!=y)
55 {
56 lop.push_back(p);
57 inlop[p]=1;
58 use+=v[p];
59 p=fa[p];
60 }
61 }
62 else {fa[y]=x,v[y]=orz[i];if(Getlop(y,i)==0)return 0;}
63 }
64 return 1;
65 }
66 void dp(int x)
67 {
68 vst[x]=1;
69 for(int i=head[x];i;i=nxt[i])
70 {
71 int y=to[i];
72 if(vst[y]||inlop[y])continue;
73 dp(y);
74 d[x]+=d[y];
75 if(!orz[i])d[x]++;
76 }
77 return ;
78 }
79 void dprt(int x)
80 {
81 vst2[x]=1;
82 for(int i=head[x];i;i=nxt[i])
83 {
84 int y=to[i];
85 if(vst2[y]||inlop[y])continue;
86 if(orz[i])f[y]=f[x]+1;
87 else f[y]=f[x]-1;
88 dprt(y);
89 }
90 return ;
91 }
92 void Getans(int x)
93 {
94 vst1[x]=1;
95 if(f[x]==now_minn){now_tot++;}
96 else if(f[x]<now_minn){now_tot=1;now_minn=f[x];}
97 for(int i=head[x];i;i=nxt[i])
98 {
99 int y=to[i];
100 if(vst1[y]||inlop[y])continue;
101 Getans(y);
102 }
103 return ;
104 }
105 void work()
106 {
107 clear();
108 // cout<<tot<<endl;
109 int n=Rd();
110 for(int i=1;i<=n;i++)
111 {
112 int a=Rd(),b=Rd();
113 add(b,a,1);
114 add(a,b,0);
115 }
116 for(int i=1;i<=2*n;i++)
117 {
118 if(dfn[i]||!head[i])continue;
119 lop.clear();sum=0;
120 use=0;
121 bool ok=Getlop(i,0);
122 if(!ok){puts("-1 -1");return ;}
123 else
124 {
125 if(!lop.size())
126 {
127 now_minn=0x7f7f7f7f;
128 now_tot=0;dp(i);
129 f[i]=d[i];
130 dprt(i);
131 Getans(i);
132 minn+=now_minn;
133 ans=ans*now_tot%mod;
134 }
135 else
136 {
137 int len=lop.size();
138 //cout<<len<<" "<<use<<endl;
139 if(use+use^len)
140 {
141 minn+=min(use,len-use);
142 for(int i=0;i<len;i++)
143 {
144 now_minn=0x7f7f7f7f;
145 now_tot=0;dp(lop[i]);
146 now_minn=d[lop[i]];
147 minn+=now_minn;
148 }
149 }
150 else
151 {
152 minn+=use;
153 ans=ans*2%mod;
154 for(int i=0;i<len;i++)
155 {
156 now_minn=0x7f7f7f7f;
157 now_tot=0;dp(lop[i]);
158 now_minn=d[lop[i]];
159 minn+=now_minn;
160 }
161 }
162 }
163 }
164 }
165 printf("%lld %lld
",minn,ans);
166 }
167 }E;
168 int main()
169 {
170 // freopen("out.in","r",stdin);
171 // freopen("b.txt","w",stdout);
172 int t=E.Rd();
173 while(t--)E.work();
174 return 0;
175 }
总结:
1.考试审题!囧
2.仔细想想自己的复杂度能不能下降,能不能避免不必要的枚举,哪怕搜索打个剪枝也是好的。
3.暴力别打错了!
4.结合着期望的复杂度去思考问题,相信自己。
下次加油!
