

排名还是假的。因为$skyh$大神没有在联考里提交代码,所以显得好像又高了一名。
总之最近发挥异常的差。脑子也不怎么动了。改题效率也降低了。
开学前夕综合症?
难得遇到一套比较简单的题,其实$200pts$应该是轻轻松松的。
然后$T3$差几分钟没写完。$T2$没判无解直接爆零(期望$70$)
思考效率很低而且有明显的前松后紧(都多少次总是有一道题没打完了。。。$T3$就留了十几分钟可还行)
T1:签到题
大意:给定序列$A,w$,称$set(x)$为从$x$开始往后,最开始集合只有${ x }$,每次找到比集合中最大元素更大的元素$A_y$就加入集合一直到序列末尾所得到的集合。
支持:给出$x$将所有$set(y)$中$x$是最小或次小元素的$w_y + = v_i$。给定$x,y$询问$( set(x) cup set(y) )cap [min(x,y) ,z]$中所有元素的$w$和。
其中$z$是$set(x)cap set(y)cap (min(x,y),n]$中的最小元素。如果不存在输出问号。$n,q le 2 imes 10^5$
题目长的可怕。需要题意转化。
我们发现如果$x$后方第一个比$A_x$大的$A_y$,那么一定有$set(x) = set(y) cup { x }$。我们把这种包含关系建边自然就会形成一棵树。
再看一眼题目的操作,就是要支持:将一个点和它所有儿子权值加。询问一条路径的权值和(如果是祖先-后代链则还要跳一下父亲)
简单树剖线段树维护。所有儿子加比较麻烦于是改成当前点加二倍,额外开一个数组表示这个点被修改的总变化量$ex$。
那么一次询问除了线段树上的值,还要$-ex_x-ex_y+ex_{lca}+ex_{fa(lca)}$。分类讨论不算太麻烦。$O(nlog^2n)$

1 #include<cstdio> 2 #define S 400005 3 int n,q,a[S],ec,fir[S],l[S],to[S];long long W[S],w[S<<2]; 4 void link(int a,int b){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;} 5 int sz[S],top[S],f[S],dfn[S],tim,dep[S],son[S],idfn[S]; 6 void dfs(int p,int fa){ 7 dep[p]=dep[fa]+1; sz[p]=1; f[p]=fa; 8 for(int i=fir[p];i;i=l[i]){ 9 dfs(to[i],p);sz[p]+=sz[to[i]]; 10 if(sz[son[p]]<sz[to[i]])son[p]=to[i]; 11 } 12 } 13 void DFS(int p,int tp){ 14 top[p]=tp; dfn[p]=++tim; idfn[tim]=p; 15 if(son[p])DFS(son[p],tp); 16 for(int i=fir[p];i;i=l[i])if(!dfn[to[i]])DFS(to[i],to[i]); 17 } 18 #define lc p<<1 19 #define rc lc|1 20 #define md (L+R>>1) 21 void build(int p=1,int L=1,int R=n+1){ 22 if(L==R){w[p]=W[idfn[L]];W[idfn[L]]=0;return;} 23 build(lc,L,md);build(rc,md+1,R);w[p]=w[lc]+w[rc]; 24 } 25 long long ask(int l,int r,int p=1,int L=1,int R=n+1){ 26 if(l<=L&&R<=r)return w[p]; 27 return (l<=md?ask(l,r,lc,L,md):0)+(r>md?ask(l,r,rc,md+1,R):0); 28 } 29 void add(int x,int v,int p=1,int L=1,int R=n+1){ 30 w[p]+=v; if(L==R)return; 31 if(x<=md)add(x,v,lc,L,md);else add(x,v,rc,md+1,R); 32 } 33 void query(int x,int y){ 34 long long ans=0;int rx=x,ry=y; 35 while(top[x]!=top[y]){ 36 if(dep[top[x]]<dep[top[y]])x^=y^=x^=y; 37 ans+=ask(dfn[top[x]],dfn[x]);x=f[top[x]]; 38 }if(dep[x]>dep[y])x^=y^=x^=y; 39 ans+=ask(dfn[x],dfn[y]); 40 if(x==rx||x==ry){if(x!=rx)rx^=ry^=rx^=ry;rx=f[rx];x=f[x];ans+=ask(dfn[x],dfn[x]);} 41 if(x==n+1||!x)puts("?"); 42 else printf("%lld ",ans-W[rx]-W[ry]+W[x]+W[f[x]]); 43 } 44 int main(){ 45 scanf("%d%d",&n,&q); 46 for(int i=1;i<=n;++i)scanf("%d",&a[i]); a[n+1]=1e9; 47 for(int i=1;i<=n;++i)scanf("%lld",&W[i]); 48 static int sta[S],top; sta[++top]=n+1; 49 for(int i=n;i;--i){ 50 while(a[sta[top]]<=a[i])top--; 51 link(sta[top],i);sta[++top]=i; 52 } 53 dfs(n+1,0);DFS(n+1,n+1);build(); 54 for(int i=1,o,x,y;i<=q;++i){ 55 scanf("%d%d%d",&o,&x,&y); 56 if(o-1)query(x,y); 57 else add(dfn[x],y*2),W[x]+=y; 58 } 59 }
T2:蓝超巨星
大意:给定$S,T$和字母映射表$f$。一次操作为循环左移$a$位然后再映射$b$次。求最少多少次操作后$S$变为T$。无法得到输出$-1$。$|S| le 2 imes 10^5,a,b le 10^9$
一次操作的字符映射可以直接倍增得到。
因为字符集只有$26$所以映射种类最多就$4 imes 9 imes 5 imes 7=1260$种之后就会循环。
所以答案上界也就是$O(1260n)$。对于每种映射把$S$断环成链维护$hash$然后模拟题意。时空复杂度都是$O(1260n)$可以得到$70pts$

1 #include<cstdio> 2 #include<vector> 3 using namespace std; 4 #define ull unsigned long long 5 #define S 200005 6 vector<ull>hsh[1888]; 7 int n,C,a,b;char f[155],s[S],t[S],F[155],g[1888][155],r[155];ull Pw=1,T; 8 ull get_hash(int f,int b){return hsh[f][b+n-1]-(b?hsh[f][b-1]:0);} 9 int main(){ 10 scanf("%d%d%d%s%s%s",&n,&a,&b,F+'a',s,t);a%=n; 11 for(char c='a';c<='z';++c)f[c]=g[0][c]=c; 12 for(int i=0;i<30;++i){ 13 if(b>>i&1){ 14 for(char c='a';c<='z';++c)r[c]=F[f[c]]; 15 for(char c='a';c<='z';++c)f[c]=r[c]; 16 } 17 for(char c='a';c<='z';++c)r[c]=F[F[c]]; 18 for(char c='a';c<='z';++c)F[c]=r[c]; 19 } 20 for(int i=1;i<=n;++i)Pw*=31; 21 while(++C){ 22 int flg=1; 23 for(char c='a';c<='z';++c)g[C][c]=f[g[C-1][c]],flg&=g[C][c]==c; 24 if(flg)break; 25 } 26 for(int i=0;i<C;++i){ 27 hsh[i].resize(n+n);hsh[i][0]=g[i][s[0]]-'a'; 28 for(int j=1;j<n;++j)hsh[i][j]=hsh[i][j-1]*31+g[i][s[j]]-'a'; 29 for(int j=0;j<n;++j)hsh[i][j+n]=hsh[i][j+n-1]*31+g[i][s[j]]-'a'; 30 for(int j=0;j<n-1;++j)hsh[i][j]*=Pw; 31 } 32 for(int i=0;i<n;++i)T=T*31+t[i]-'a'; 33 int ans=0,f=0,b=0; 34 while(f=f==C-1?0:f+1,b+=a,b-=b>=n?n:0,++ans&&ans<=30000000)if(get_hash(f,b)==T)return printf("%d ",ans),0; 35 puts("-1"); 36 }
还是断环成链。我们枚举最终循环位移了$x$位,如果答案是$q$可以得到一个$aq equiv x (mod n)$的式子。
如果$a | gcd(x,n)$那么就把$a,x,n$都除掉这个$gcd$,否则无解。
现在互质了就有逆元了,我们就得到了一个形如$q equiv r(mod n)$的式子。
再去考虑字符映射的问题,我们搞一下那个$last_i$表示$s_i$上一次出现位置。维护$i-last_i$序列的哈希值。
预处理映射表上的环上任意两种字母的距离。这个字符串能变成$T$仅当哈希值与$T$一致。
然后如果哈希值一样那么就可以根据原有和现有的字符的距离列出另一些同余方程。
如果满足所有同余方程那么就可以更新答案了。暴力解$27$个同余方程可以做到很不满的$O(26^2)$
考虑每次$x$增加一位,就会把序列开头的一个字符删掉,影响是这个字符下一次出现时的$i-last_i$值变化了。
暴力修改一下。然后结尾填一个字符也很简单。写写就完了。$O(26^2n)$

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ull unsigned long long 4 #define S 400005 5 int n,C,a,b,res[155][155],lp[155],clp[S]; 6 char f[155],s[S],t[S],F[155],g[1888][155],r[155];ull pw[S],Th,Sh; 7 int R[28],M[28],cnt,ans=1<<30; 8 int gcd(int x,int y){return y?gcd(y,x%y):x;} 9 void exgcd(int a,int b,int&x,int&y){ 10 if(!b){x=1;y=0;return;} 11 exgcd(b,a%b,x,y);int r=x;x=y;y=r-a/b*x; 12 } 13 int inv(int x,int m){int a,b;exgcd(x,m,a,b);return (a%m+m)%m;} 14 void solve(){ 15 for(int i=2;i<=cnt;++i){ 16 int lcm=M[i]/gcd(M[i],M[i-1])*M[i-1]; 17 if(M[i]<M[i-1])swap(M[i],M[i-1]),swap(R[i],R[i-1]); 18 while(R[i]<lcm&&R[i]%M[i-1]!=R[i-1])R[i]+=M[i]; 19 if(R[i]>=lcm)return;M[i]=lcm; 20 }if(!R[cnt])R[cnt]=M[cnt]; 21 ans=min(ans,R[cnt]); 22 } 23 set<int>pl[155]; 24 int main(){ 25 scanf("%d%d%d%s%s%s",&n,&a,&b,F+'a',s+1,t+1);a%=n; 26 for(char c='a';c<='z';++c)f[c]=g[0][c]=c; 27 for(int i=0;i<30;++i){ 28 if(b>>i&1){ 29 for(char c='a';c<='z';++c)r[c]=F[f[c]]; 30 for(char c='a';c<='z';++c)f[c]=r[c]; 31 } 32 for(char c='a';c<='z';++c)r[c]=F[F[c]]; 33 for(char c='a';c<='z';++c)F[c]=r[c]; 34 } 35 for(int i=pw[0]=1;i<=n;++i)pw[i]=pw[i-1]*31331; 36 for(char c='a';c<='z';++c){ 37 char x=c; 38 do res[c][f[x]]=res[c][x]+1,x=f[x];while(x!=c); 39 } 40 for(int i=1;i<=n;++i)Th=Th*31331+(lp[t[i]]?i-lp[t[i]]:0),lp[t[i]]=i; 41 for(char c='a';c<='z';++c)lp[c]=0; 42 for(int i=1;i<=n;++i)pl[s[i]].insert(i); 43 for(int i=1;i<=n;++i)Sh=Sh*31331+(lp[s[i]]?clp[i]=i-lp[s[i]]:0),lp[s[i]]=i; 44 int g=gcd(a,n),iv=inv(a/g,n/g); 45 for(int i=1;i<=(g==n?1:n);++i){ 46 if(Sh!=Th||(g!=n&&(i-1)%g))goto F; 47 if(cnt=g!=n)M[1]=n/g,R[1]=(i-1ll)/g*iv%M[1]; 48 for(char c='a';c<='z';++c)if(pl[c].size()){ 49 int x=*pl[c].begin(); 50 if(!res[c][t[x-i+1]])goto F; 51 cnt++;R[cnt]=res[c][t[x-i+1]]%res[c][c];M[cnt]=res[c][c]; 52 } 53 solve(); F:; 54 pl[s[i]].erase(i); 55 if(pl[s[i]].size()){ 56 int x=*pl[s[i]].begin(); 57 Sh-=clp[x]*pw[n-1+i-x]; 58 }else lp[s[i]]=0; 59 Sh=Sh*31331+(lp[s[i]]?clp[i+n]=i+n-lp[s[i]]:0),lp[s[i]]=i+n; 60 pl[s[i]].insert(i+n); 61 }printf("%d",ans>>30&1?-1:ans); 62 }
T3:秘密行动
大意:要求你随意确定一个长为$n$的序列$A$。有一个质数集合$S$,$|S|=10$。对于$A$序列的每个位置$i$,对于每个集合中的质数$p$。
如果$p|A_i$则会产生$C_{p,i}$代价。否则会产生$D_{p,i}$代价。然后还有$m$对关系,给定$a,b,p(p in |S|)$如果$p | lcm(A_a,A_b) ,p ot | gcd(A_a,A_b) $则会产生$F_p$代价。
你任意确定$A_{1...n}$的值,最小化所有的代价之积。$n le 50,eps le 10^{-5},m le 500$。
所有东西都乘起来不好算,于是我们算加起来的就好了。就是一个草率的$ln$再$exp$的过程。
然后发现,就是对于每个点,可以选或不选,都有一定代价,然后如果一个选了一个不选那么会产生额外代价。
很经典的网络流。但是这一次不知道为啥建图可能会出锅。就是最大权闭合子图的那两种建图方式并不是等价的。
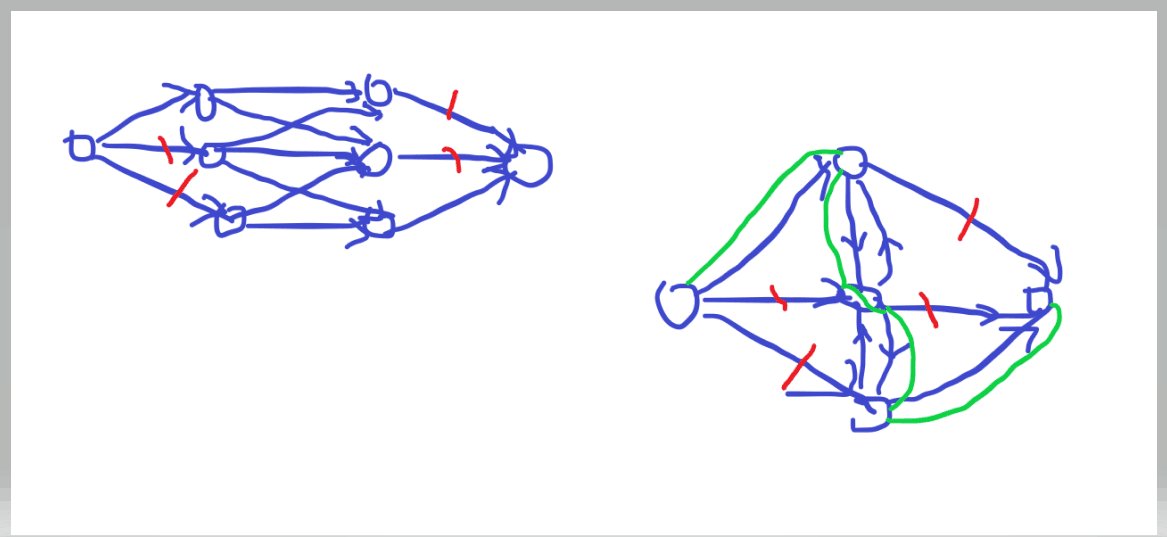
就例如在这个图里,虽然割断了一样的边集,但是左边那个没有增广路了而右边绿色的增广路依旧存在。左图显然是非法的。
还是需要具体问题具体分析。

1 #include<cstdio> 2 #include<cmath> 3 #include<iostream> 4 using namespace std; 5 #define eps 1e-9 6 #define S 10000005 7 int n,m,o[55][10],pc;double F[11],ans; 8 int fir[S],l[S],to[S],ec=1,d[S];double w[S]; 9 void link(int a,int b,double v){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;w[ec]=v;} 10 void con(int a,int b,double v){link(a,b,v);link(b,a,0);} 11 bool bfs(){ 12 static int q[S]; 13 for(int i=1;i<=pc;++i)d[i]=1e9; 14 for(int h=1,t=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(w[i]>eps&&d[to[i]]>d[q[h]]+1) 15 d[q[++t]=to[i]]=d[q[h]]+1; 16 return d[1]<pc; 17 } 18 double dfs(int p,double f){ 19 double r=f; 20 if(p==1)return f; 21 for(int i=fir[p];i&&r>eps;i=l[i])if(d[to[i]]==d[p]+1&&w[i]>eps){ 22 double x=dfs(to[i],min(r,w[i])); 23 if(x<eps)d[to[i]]=0; 24 w[i]-=x;w[i^1]+=x;r-=x; 25 }return f-r; 26 } 27 int main(){ 28 scanf("%d%d",&n,&m);pc=1; 29 for(int i=1;i<=n;++i)for(int j=0;j<=9;++j)o[i][j]=++pc; 30 for(int i=0;i<=9;++i)scanf("%*d%lf",&F[i]),F[i]=log(F[i]); 31 for(int i=1;i<=n;++i){ 32 double x; 33 for(int j=0;j<=9;++j)scanf("%lf",&x),con(0,o[i][j],log(x)); 34 for(int j=0;j<=9;++j)scanf("%lf",&x),con(o[i][j],1,log(x)); 35 } 36 for(int i=1;i<=m;++i){ 37 int a,b,c;scanf("%d%d%d",&a,&b,&c);c--; 38 con(o[a][c],o[b][c],F[c]);con(o[b][c],o[a][c],F[c]); 39 } 40 while(bfs())ans+=dfs(0,1e9); 41 printf("%.9lf ",exp(ans)); 42 }
