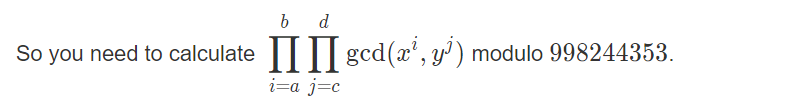
给定 a ,b ,c , d , x, y 求上式
0⩽a,b,c,d⩽3×106,0<x,y⩽109,a⩽b,c⩽d.
首先对问题转化为枚举质因子,计算为每个公共质因子贡献的问题。(由唯一分解定理容易想到)
规模为O(log x + log y)乘积就转化成了和的形式

只需求出此式(指数)然后快速幂即可。
注意到min函数良好的性质可以枚举一维,另一维O(1)得出。
ll a, b, c, d, x, y; ll ans; void solve(int p) { ll aa = 0, bb = 0; while (x % p == 0) x /= p, aa++; while (y % p == 0) y /= p, bb++; if (!aa || !bb) return; ll tmp = 0; for (ll i = a; i <= b; i++) { ll j = aa * i / bb; ll cur, now; if (j < c) cur = (d - c + 1) * i % Mod * aa % Mod; else if (j >= d) cur = (c + d) * (d - c + 1) / 2 % Mod * bb % Mod; else now = (c + j) * (j - c + 1) / 2 % Mod * bb % Mod, cur = (now + (d - j) * i % Mod * aa % Mod) % Mod; tmp = (tmp + cur) % Mod; } ans = ans * quickPower(p, tmp, MOD) % MOD; } int main() { ans = 1ll; a = readll(); b = readll(); c = readll(); d = readll(); x = readll(); y = readll(); for (int k = 2; k <= x; k++) if (x % k == 0) solve(k); if (x > 1) solve(x); Put(ans); }