在圆上一点S,扔出一个球,这个球经过N次反弹还有可能回到S点。N = 4时,有4种扔法,如图:
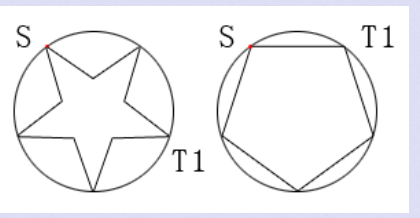
恰好经过4次反弹回到起点S(从S到T1,以及反向,共4种)。
给出一个数N,求有多少种不同的扔法,使得球恰好经过N次反弹,回到原点,并且在第N次反弹之前,球从未经过S点。
输入一个数N(1 <= N <= 10^9)。
直接模拟肯定是不行的。
注意到每次反弹的点必然是圆上的n等分点,那么相当于每次可以对一个等分点射击,抽象成数轴上选点然后跳。 有点类似Polya计数那题,有个结论是循环的个数是 gcd(n,i),循环长度是n / gcd(n,i)。因此求出n+1的欧拉函数就好了