C:给两个栈,每次只能取栈顶元素,取完后自动pop 问能取到最多几个元素
栈中元素之和必须小于等于K
官方题解给出的做法是O(N+M) 受上一场CF启发,此题可以很自然联想到二分做法。 二分答案,答案显然具有单调性。check函数只需遍历一遍可能情况
复杂度O((N+M)logX)

int n, m; ll k; ll a[maxn], b[maxn]; ll sum1[maxn]; ll sum2[maxn]; bool check(int x) { for (int i = x - m ; i <= min(x,n); i++) { if (sum1[i] + sum2[x - i] <= k) { //cout << x << " " << i <<" "<< x - i << endl; return 1; } } return 0; } int main() { scanf("%d%d%lld", &n, &m, &k); for (int i = 1; i <= n; i++) { scanf("%lld", a + i ); sum1[i] = sum1[i - 1] + a[i]; } for (int i = 1; i <= m; i++) { scanf("%lld", b + i); sum2[i] = sum2[i - 1] + b[i]; } int l = 0, r = n + m; while (l < r) { int mid = l + r + 1 >> 1; if (check(mid)) l = mid; else r = mid - 1; } if (check(l)) printf("%d", l); else printf("%d", l-1); }
D:
函数F(x) 表示x的因子个数 。 求 sgma i*F(i) N<=1e7
利用d(i)==(每个质因数的指数+1)的积 跑一遍素数筛顺便可筛出F函数,之后相乘即可

int n; ll d[maxn], minn[maxn], prime[maxn]; bool is[maxn]; int tot; void init() { d[1] = 1; for (int i = 2; i <= n; i++) { if (is[i] == 0) prime[++tot] = i, d[i] = 2, minn[i] = 1; for (re int j = 1; prime[j] * i <= n && j <= tot; j++) { is[i * prime[j]] = 1; if (i % prime[j] == 0) { minn[i * prime[j]] = minn[i] + 1; d[i * prime[j]] = d[i] / (minn[i] + 1) * (minn[prime[j] * i] + 1); break; } minn[i * prime[j]] = 1; d[i * prime[j]] = d[i] * 2; } } } int main() { scanf("%d", &n); init(); ll res = 0; for (int i = 1; i <= n; i++) { res += i * d[i]; } printf("%lld", res); }
E:
构造一对数组a,b 要求满足 数组中数字均不超过M。 且 1.a中元素互不相同 2.b中元素互不相同 3.ai不等于bi 问可构造出多少对
1<=N<=M<=5e5
推公式即可 先把a数组定下来,有A(n,m) 种选法。 再考虑所有情况减去不对的情况。 故容斥(实际上是错排的推广)
注意最后不对的情况要除以(m-n)!去重
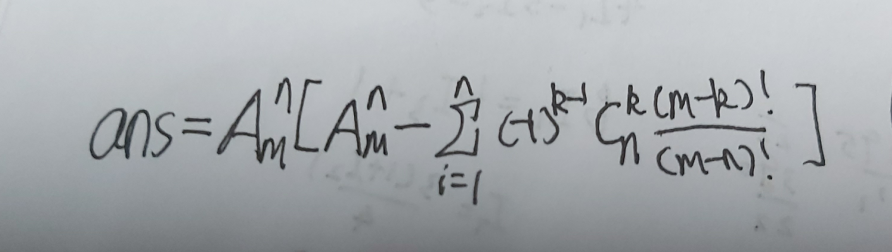
注意取逆元。

ll inv[maxn]; ll n, m; void inver(ll p) { inv[0] = 1; inv[1] = 1; for (int i = 2; i <= m; i++) { inv[i] = (p - p / i) * inv[p % i] % p; } } ll c[maxn]; ll fac[maxn]; ll quickPower(ll a, ll b, ll m) { //计算a的b次方 ll ans = 1; ll base = a; while (b) { if (b & 1) { ans *= base; ans %= m; } base *= base; base %= m; b >>= 1; //注意是b>>=1 not b>>1 } return ans; } ll get_inv(ll x) { return quickPower(x, MOD - 2, MOD); } void get_fac() { fac[0] = 1; for (int i = 1; i <= m; i++) { fac[i] = (fac[i - 1] * i)%MOD; } } void get_C(ll n) { c[0] = 1; for (int i = 0; i < n; i++) c[i + 1] = ((c[i] * (n - i)) % MOD * inv[i + 1]) % MOD; } int main() { scanf("%lld%lld", &n, &m); inver(MOD); get_fac(); get_C(n); ll res = (1 * ((fac[m] * get_inv(fac[m - n])) % MOD * get_inv(fac[m - n])) % MOD)%MOD; ll tmp = fac[m]; int f = 1; for (int i = 1; i <= n; i++) { tmp = (tmp + ((-1ll * f) * ((c[i] * fac[m - i]) % MOD))+MOD) % MOD; f *= -1; } //cout << res << tmp << endl; printf("%lld", (tmp * res) % MOD); }
F:
NIm博弈 不同之处在于 后手者可以在游戏开始前取出第一堆中的若干个放到第二堆中 问最少放几个可以保证他必胜 若不能输出-1
2<=N<=300 1<=ai<=1e12

ll a[305]; ll m, s; int main() { int n; scanf("%d", &n); for (int i = 0; i < n; i++) scanf("%lld", a + i); m = a[2]; for (int i = 3; i < n; i++) m ^= a[i]; s = a[0] + a[1]; ll rem = s - m; if ((rem % 2) || (rem < 0)) { puts("-1"); return 0; } rem /= 2; ll b = rem; int f = 1; for (ll i = 50; i >= 0; i--) { ll p = 1ll << i; if ((m & p) && (rem & p)) f = 0; if ((m & p) && ((b + p) <= a[0])) b += p; } b = a[0] - b; if ((b >= a[0]) || (b < 0)) f = 0; if (f) printf("%lld", b); else puts("-1"); }
