线段树
什么时候用线段树
1.统计量可合并
2.修改量可合并
3.通过统计量可直接修改统计量
一句话:满足区间加法即可使用线段树维护信息
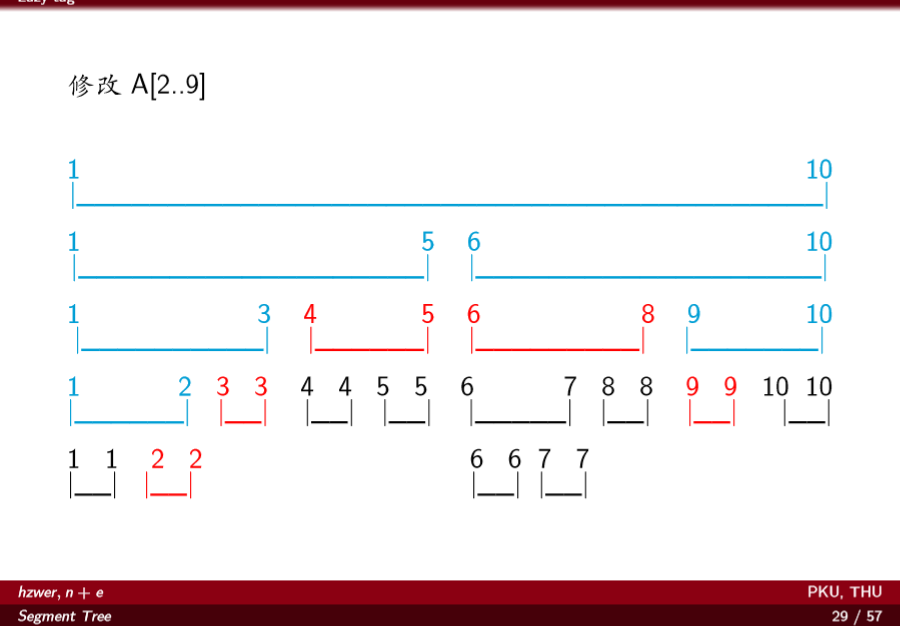
理解Lazy Tage
蓝色是要把信息及时维护的节点,红色是本次区间修改操作Lazy Tage下传停止的位置。
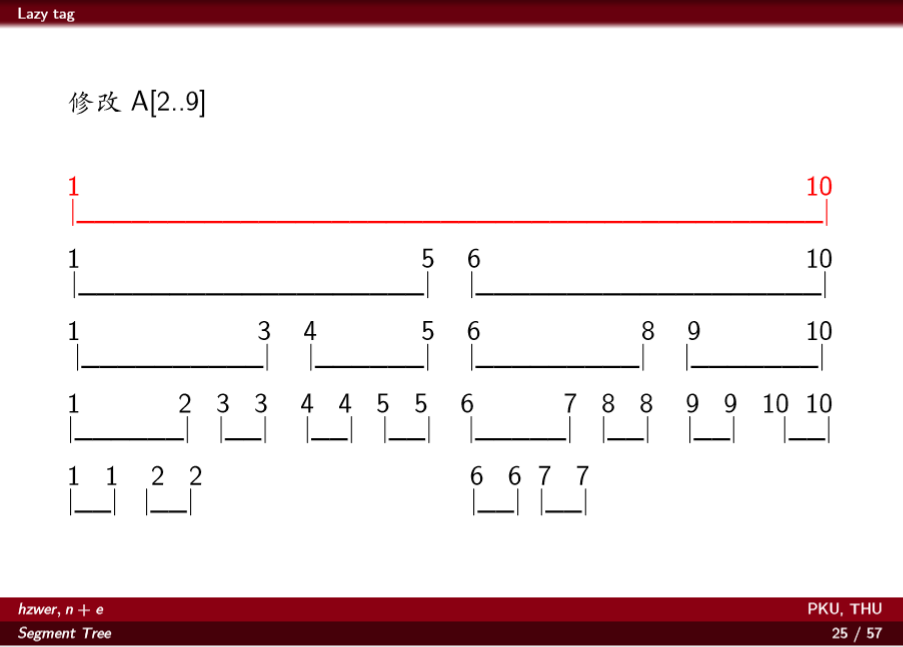
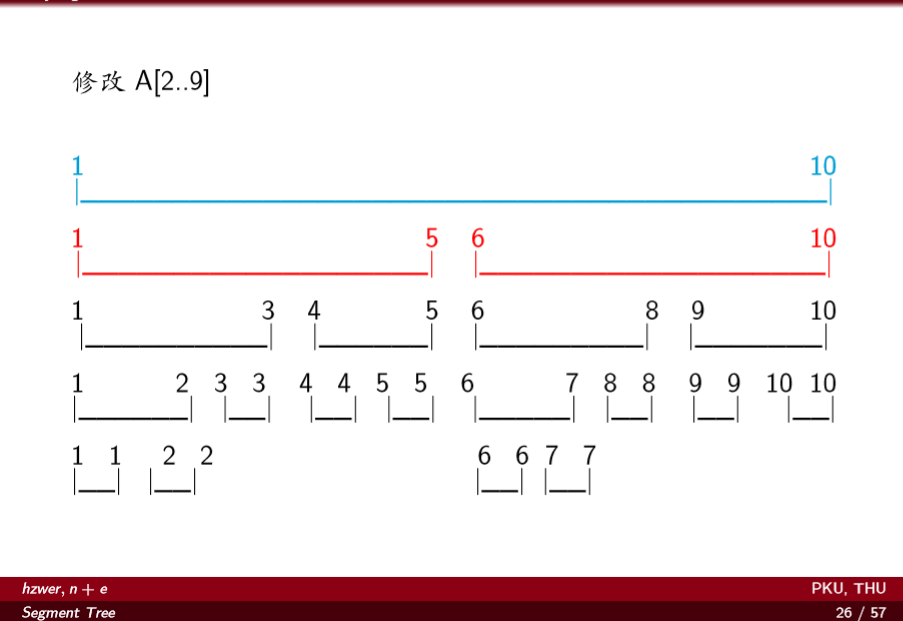
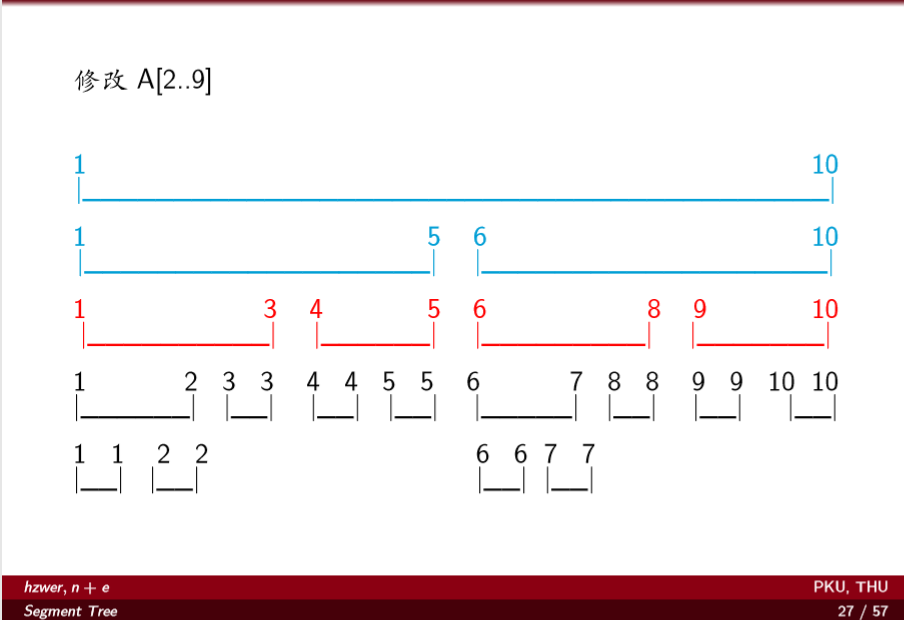
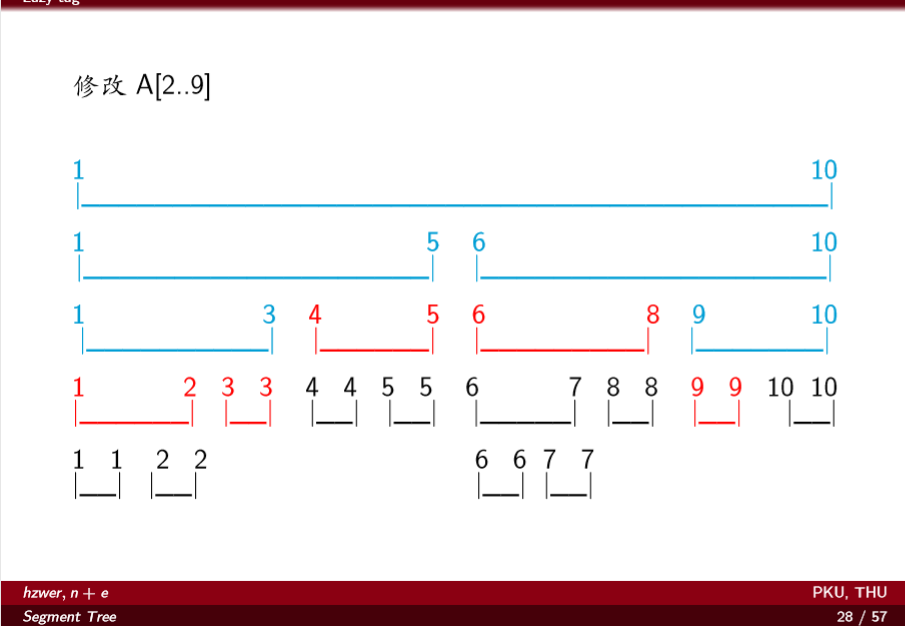
模板 Just a Hook HDU-1698
#include<iostream> #include<cstdio> #include<algorithm> #include<vector> #include<queue> using namespace std; const int maxn = 100050 * 4; //线段树范围开4倍 struct Tree { int l, r, sum, maxx; }; Tree node[maxn]; int a[maxn]; int lazy[maxn]; void Pushdown(int rt, int m) { if (lazy[rt]) { lazy[rt << 1] = lazy[rt]; lazy[rt << 1 | 1] = lazy[rt]; node[rt << 1].sum = lazy[rt] * (m - (m >> 1)); node[rt << 1 | 1].sum = lazy[rt] * (m >> 1); lazy[rt] = 0; } } void Pushup(int i) { node[i].sum = node[i << 1].sum + node[i << 1 | 1].sum; node[i].maxx = max(node[i << 1].maxx, node[i << 1 | 1].maxx); } void Build(int i, int l, int r) { lazy[i] = 0; node[i].l = l; node[i].r = r; if (l == r) { node[i].maxx = a[l]; node[i].sum = a[l]; return; } int mid = l + r >> 1; Build(i << 1, l, mid); Build(i << 1 | 1, mid + 1, r); Pushup(i); } int getsum(int i, int l, int r) { if (node[i].l == l && node[i].r == r) return node[i].sum; int mid = node[i].l + node[i].r >> 1; Pushdown(i, node[i].r - node[i].l + 1); if (r <= mid) return getsum(i << 1, l, r); else if (l > mid) return getsum(i << 1 | 1, l, r); else return getsum(i << 1, l, mid) + getsum(i << 1 | 1, mid + 1, r); } void update(int i, int l, int r,int v) { if (node[i].r == r && node[i].l == l) { lazy[i] = v; node[i].sum = v * (r - l + 1); return; } if(node[i].l == node[i].r) return; int mid = node[i].l + node[i].r >> 1; Pushdown(i, node[i].r - node[i].l + 1); if (r <= mid) update(i << 1, l, r, v); else if (l > mid) update(i << 1 | 1, l, r, v); else { update(i << 1, l, mid, v); update(i << 1 | 1, mid + 1, r, v); } Pushup(i); } int main() { int kase = 1; int m, n, x, y, z, q; string op; int T; scanf("%d", &T); while (T--) { scanf("%d%d", &n, &q); for (int i = 1; i <= n; i++) a[i] = 1; Build(1, 1, n); while (q--) { scanf("%d%d%d", &x, &y, &z); update(1, x, y, z); } printf("Case %d:The total value of the hook is %d.\n", kase, getsum(1, 1, n)); kase++; } return 0; }
“树状数组支持的操作:1、区间和、区间异或和、区间乘积和RMQRMQ(显然,支持的操作都具有交换律,这也算是树状数组的一大特性吧)2、单点修改 ”

code
#include<iostream> #include<cstdio> #include<string> #include<algorithm> #include<queue> #include<set> #include<map> #include<cmath> const double PI = acos(-1.0); #define INF 0x3f3f3f3f typedef long long ll; using namespace std; int n, m, tree[2000010]; inline int lowbit(int k) { //lowbit(x)是x的二进制表达式中最低位的1所对应的值 return k & -k; } void add(int x, int k) { while (x <= n) { tree[x] += k; x += lowbit(x); } } int sum(int x) { int ans = 0; while (x) { ans += tree[x]; x -= lowbit(x); } return ans; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) { int a; scanf("%d", &a); add(i, a); } for (int i = 1; i <= m; i++) { int a, b, c; scanf("%d%d%d", &a, &b, &c); if (a == 1) add(b, c); if (a == 2) printf("%d", sum(c) - sum(b - 1)); } return 0; }