T122393 À la Volonté du Peuple:
题意:初始点为1,火从初始点向周围扩散,当两堆火相遇便会爆炸(可以自环),给点和边和边权,问爆炸点的数量。
分析:如果爆炸点在点上,那么该点至少有两条最短路能到达,如果爆炸点在边上,那么这条边不在最短路上。该做法的正确性分析:对于点,最短路意味着最先到达,如果有多个火同时最先到达,那么该点必爆。对于边,如果这条边不在最短路的路线当中,那么这条边的两个端点必然有另外一条最短路能够到达,当火从那两条最短路到达这两个点之后,两堆火必然会在连接这两个点的这条路上相遇,从而这条路不是最短路的话一定有个点会在这条路上爆炸,相反如果这条路是最短路,那么火一定是最先到达并走过这条路的,不会在这条路上相遇。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn = 1e6+5; 4 const int maxm = 3*1e5+5; 5 const int inf = 0x3f3f3f3f; 6 int n,m; 7 struct edge{ 8 int to,w; 9 edge(int a,int b){ 10 to = a,w = b; 11 } 12 }; 13 struct node{ 14 int id,dis; 15 node(int a,int b){ 16 id = a,dis = b; 17 } 18 friend bool operator <(const node &a,const node &b){ 19 return a.dis > b.dis; 20 } 21 }; 22 vector <edge> e[maxn]; 23 int vis[maxm],dis[maxm]; 24 void dijkstra(){ 25 int s = 1; 26 for (int i = 0; i <= n; i++) dis[i] = inf,vis[i] = 0; 27 dis[s] = 0; 28 priority_queue<node> q; 29 q.push(node(s,dis[s])); 30 while (!q.empty()){ 31 node u = q.top(); q.pop(); 32 if (vis[u.id]) continue; 33 vis[u.id] = 1; 34 for (int i = 0; i < e[u.id].size(); i++){ 35 edge y = e[u.id][i]; 36 if (vis[y.to]) continue; 37 if (dis[y.to] > dis[u.id] + y.w) 38 dis[y.to] = u.dis + y.w; 39 q.push(node(y.to,dis[y.to])); 40 } 41 } 42 } 43 int main(){ 44 scanf("%d%d",&n,&m); 45 for (int i = 1,f,t,w; i <= m; i++){ 46 scanf("%d%d%d",&f,&t,&w); 47 e[f].push_back(edge(t,w)); 48 if (f!=t) e[t].push_back(edge(f,w)); 49 } 50 dijkstra(); 51 int cnt,ans = 0; 52 for (int i = 1; i <= n; i++){ 53 cnt = 0;//统计到i点的最短路数量 54 for (int j = 0; j < e[i].size(); j++){ 55 int w = e[i][j].w,to = e[i][j].to; 56 if (dis[i] == w + dis[to]) cnt++; 57 else if (i >= to && dis[i] + w > dis[to] && dis[to] + w > dis[i]) ans++;//i>=to是判重 58 } 59 if (cnt > 1) ans++; 60 } 61 printf("%d ",ans); 62 return 0; 63 }
T122394 Billionaire:
题意:给一个数和今天的日期,从明天开始每天对这个数加x(x = 1,2,3,4,5……随天数+1而+1)问哪天能够到达1e9,输出日期。
分析:模拟即可,T有点大需要二分一下不然超时。或者套用zeller公式可以直接得出结果。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const ll maxn = 1e9; 5 const int maxm = 1e5; 6 ll sum[maxm]; 7 void init(){ 8 for (int i = 0; i < maxm; i++){ 9 sum[i] = i; 10 } 11 for (int i = 1; i < maxm; i++){ 12 sum[i] += sum[i-1]; 13 } 14 } 15 bool check(int y){ 16 if ((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)) return true; 17 else return false; 18 } 19 int mo[12] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; 20 int main(){ 21 init(); 22 int t; 23 scanf("%d",&t); 24 while (t--){ 25 int y,m,d; 26 ll M; 27 scanf("%lld %d %d %d",&M,&y,&m,&d); 28 ll u = maxn - M; 29 int pos = lower_bound(sum,sum+maxm,u)-sum; 30 int cnt = pos; 31 while (1){ 32 int tmp; 33 if ((check(y)&&m<=2)||(check(y+1)&&m>2)) tmp = 366; 34 else tmp = 365; 35 if (cnt < tmp) break; 36 else { 37 cnt -= tmp; 38 y++; 39 if (m==2&&d==29){ 40 m = 3; d = 1; 41 } 42 } 43 } 44 int t = m-1; 45 while (1){ 46 if (check(y)) mo[1] = 29; 47 else mo[1] = 28; 48 if (d+cnt>mo[t]){ 49 cnt -= (mo[t]-d+1); 50 d = 1; 51 t++; 52 t %= 12; 53 if (t==0) y++; 54 } 55 else{ 56 d += cnt; 57 break; 58 } 59 } 60 printf("%d %d %d ",y,t+1,d); 61 } 62 return 0; 63 }
题解给的zeller公式版

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int getId(int y, int m, int d) { 5 if (m < 3) {y --; m += 12;} 6 return 365 * y + y / 4 - y / 100 + y / 400 + (153 * (m - 3) + 2) / 5 + d - 307; 7 } 8 vector<int> date(int id) { 9 int x = id + 1789995, n, i, j, y, m, d; 10 n = 4 * x / 146097; 11 x -= (146097 * n + 3) / 4; 12 i = (4000 * (x + 1)) / 1461001; x -= 1461 * i / 4 - 31; 13 j = 80 * x / 2447; d = x - 2447 * j / 80; x = j / 11; 14 m = j + 2 - 12 * x; y = 100 * (n - 49) + i + x; 15 return vector<int>({y, m, d}); 16 } 17 18 19 void work() { 20 int M, y, m, d; 21 scanf("%d%d%d%d", &M, &y, &m, &d); 22 int id = getId(y, m, d); 23 int l = 0, r = sqrt(2e9); 24 while (l < r) { 25 int mid = (l + r) / 2; 26 int v = M + (0 + mid) * (mid + 1) / 2; 27 if (v >= 1000000000) r = mid; 28 else l = mid + 1; 29 } 30 id += l; 31 auto ret = date(id); 32 printf("%d %d %d ", ret[0], ret[1], ret[2]); 33 } 34 35 int main() { 36 int T; 37 scanf("%d", &T); 38 while (T--) work(); 39 }
T122395 Counting K-ary Palindromes:
先放弃,待更新。
题解代码先放这:

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 typedef pair<int, int> pii; 5 #define read(a) scanf("%d", &a) 6 #define x first 7 #define y second 8 9 #define MOD 998244353 10 11 LL power(LL x, LL y, LL z) { 12 LL ret = 1; 13 for ( x %= z; y; y >>= 1) { 14 if (y & 1) ret = ret * x % z; 15 x = x * x % z; 16 } 17 return ret; 18 } 19 20 LL n; 21 int p, K; 22 23 void init(vector <int> & a) { 24 a.clear(); 25 a.resize(p); 26 a[0] = 1; 27 } 28 29 void upd(vector <int> &a, LL b, int st = 0) { 30 int x; 31 if (b == n - b - 1) { 32 x = int(power(K, b, p)) % p; 33 } else { 34 x = int(power(K, b, p) + power(K, n - b - 1, p)) % p; 35 } 36 vector <int> c; 37 c.resize(p); 38 for (int i = st; i < K; i++) { 39 for (int j = 0; j < p; j++) { 40 (c[(j + i * x) % p] += a[j]) %= MOD; 41 } 42 } 43 swap(a, c); 44 } 45 46 void mul(vector <int> &a, vector <int> &b) { 47 vector <int> c; 48 c.resize(p); 49 for (int i = 0; i < p; i++) 50 for (int j = 0; j < p; j++) { 51 int x = (i + j) % p; 52 c[x] = int((c[x] + (LL)a[i] * b[j]) % MOD); 53 } 54 swap(a, c); 55 } 56 57 void power(vector <int> &a, long long b) { 58 vector <int> ret; 59 init (ret); 60 for ( ; b; b >>= 1 ) { 61 if (b & 1) mul(ret, a); 62 mul(a, a); 63 } 64 swap(a, ret); 65 } 66 67 vector <int> ans, tr; 68 69 int main() { 70 scanf("%lld%d%d", &n, &p, &K); 71 if (n == 1) { 72 int aa = 0; 73 for (int i = 0; i < K; i++) { 74 if (i % p == 0) aa ++; 75 } 76 cout << aa << endl; 77 return 0; 78 } 79 LL sz = n / 2 - 1; 80 if (K % p == 0) { 81 cout << (K / p - 1) * power(K, sz + (n & 1), MOD) % MOD << endl; 82 return 0; 83 } 84 init(ans); 85 init(tr); 86 LL tot = sz / (p - 1); 87 if (tot) { 88 for (int i = 2; i <= p; i++) { 89 upd(tr, i - 1); 90 } 91 power(tr, tot); 92 mul(ans, tr); 93 } 94 upd(ans, 0, 1); 95 for (long long i = 2 + tot * (p - 1); i <= (n + 1) / 2; i++) { 96 upd(ans, i - 1); 97 } 98 printf("%d ", ans[0]); 99 }
T122396 Deceiver:
题意:给两个整数a,b。gcd(a,b) = 1。给一个k,问x、y均>=0且为整数时 ax+by=c 无解的第k小c。(参考小凯的疑惑)
分析:待更新。
题解代码先放这:

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 typedef long long LL; 5 6 LL solve(LL n, LL a, LL b, LL m) { 7 if (b == 0) return n * (a / m); 8 if (a >= m) return n * (a / m) + solve(n, a % m, b, m); 9 if (b >= m) return (n - 1) * n / 2 * (b / m) + solve(n, a, b % m, m); 10 return solve((a + b * n) / m, (a + b * n) % m, m, b); 11 } 12 13 LL A, B, K; 14 15 void work() { 16 scanf("%lld%lld%lld", &A, &B, &K); 17 LL l = 1, r = (double)A * B > 3e18 ? 2e18 + 10 : min(LL(2e18) + 10, A * B - 1); 18 assert(double(A - 1) * (B - 1) / 2 >= K); 19 while (l < r) { 20 LL mid = (l + r) / 2; 21 LL n = mid / A + 1, m = B, a = mid - (n - 1) * A + B, b = A; 22 LL tot = solve(n, a, b, m) - 1; 23 LL cnt = mid - tot; 24 if (cnt >= K) r = mid; 25 else l = mid + 1; 26 } 27 printf("%lld ", l); 28 } 29 30 int main() { 31 int T; 32 scanf("%d", &T); 33 while (T--) work(); 34 }
T122397 Everybody deserves a long long name:
题意:给一堆英文,换成编译器能读懂的语言。
分析:文本编辑器查找替换即可。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 int main(){ 5 string name; 6 cin>>name; 7 if ( name[0] != 'g') { reverse(name.begin(),name.end());} else { name += 'h';} 8 if ( name[name.length()-1] != 'y' && name[0] == 'w') { name += 'j';} else { name += 't';} 9 if ( name.length() <= 42) { name += 'u';} else { ;} 10 if ( name[name.length()-1] != 'v') { reverse(name.begin(),name.end());} else { name += 'd';} 11 if ( name.length() <= 43) { name += 'o';} else { name += 'q';} 12 if ( name[0] != 'm') { reverse(name.begin(),name.end());} else { reverse(name.begin(),name.end());} 13 if ( name[name.length()-1] == 'x') { ;} else { name += 's';} 14 if ( name.length() < 22) { name += 'n';} else { name += 't';} 15 if ( name[0] != 'i') { ;} else { reverse(name.begin(),name.end());} 16 if ( name[name.length()-1] == 'c') { name += 'e';} else { name += 'a';} 17 if ( name.length() != 42 && name[name.length()-1] == 'v') { name += 'u';} else { ;} 18 if ( name.length() >= 47) { name += 'j';} else { reverse(name.begin(),name.end());} 19 if ( name[0] != 'v') { name += 'e';} else { name += 'd';} 20 if ( name[name.length()-1] == 'y') { name += 'w';} else { reverse(name.begin(),name.end());} 21 if ( name[0] == 'u') { reverse(name.begin(),name.end());} else { name += 'i';} 22 if ( name.length() >= 32) { name += 'w';} else { ;} 23 if ( name[name.length()-1] != 'i' && name[0] == 'd') { name += 'a';} else { reverse(name.begin(),name.end());} 24 if ( name[name.length()-1] != 'y') { reverse(name.begin(),name.end());} else { ;} 25 if ( name[0] == 'y') { name += 'v';} else { reverse(name.begin(),name.end());} 26 if ( name.length() > 50) { ;} else { name += 'm';} 27 if ( name[name.length()-1] == 't') { name += 'w';} else { name += 'q';} 28 if ( name[0] == 't') { name += 'e';} else { ;} 29 if ( name.length() > 48) { name += 'l';} else { reverse(name.begin(),name.end());} 30 if ( name[name.length()-1] == 'y') { name += 'w';} else { reverse(name.begin(),name.end());} 31 if ( name.length() >= 18 && name[0] != 'b') { reverse(name.begin(),name.end());} else { name += 'c';} 32 if ( name.length() > 18) { name += 'y';} else { ;} 33 if ( name[name.length()-1] != 'g') { name += 'a';} else { reverse(name.begin(),name.end());} 34 if ( name[0] == 'q') { ;} else { name += 'i';} 35 if ( name[name.length()-1] == 'n' && name.length() >= 38) { name += 'o';} else { name += 'v';} 36 if ( name[0] != 'n') { ;} else { name += 'z';} 37 if ( name.length() == 21 && name[0] != 'm') { name += 'u';} else { name += 'o';} 38 if ( name.length() == 34) { ;} else { name += 'z';} 39 if ( name[0] != 'r') { reverse(name.begin(),name.end());} else { reverse(name.begin(),name.end());} 40 if ( name.length() > 25) { name += 'c';} else { reverse(name.begin(),name.end());} 41 if ( name[0] != 'u') { name += 'k';} else { name += 'l';} 42 if ( name.length() < 41) { reverse(name.begin(),name.end());} else { name += 'p';} 43 if ( name[0] != 'p') { reverse(name.begin(),name.end());} else { name += 'z';} 44 if ( name.length() < 4 && name[name.length()-1] == 'p') { reverse(name.begin(),name.end());} else { name += 'l';} 45 if ( name.length() != 16 && name[0] == 'w') { name += 'r';} else { name += 'o';} 46 if ( name[name.length()-1] == 'c') { name += 'p';} else { name += 'i';} 47 if ( name.length() != 20) { name += 'p';} else { reverse(name.begin(),name.end());} 48 if ( name[name.length()-1] != 'b') { reverse(name.begin(),name.end());} else { name += 'p';} 49 if ( name[0] != 'c') { name += 'n';} else { name += 'l';} 50 if ( name.length() <= 40) { name += 'd';} else { ;} 51 if ( name[0] == 'g') { name += 'y';} else { name += 'i';} 52 if ( name[name.length()-1] == 'k') { reverse(name.begin(),name.end());} else { name += 'v';} 53 if ( name.length() != 20 && name[0] != 'u') { reverse(name.begin(),name.end());} else { reverse(name.begin(),name.end());} 54 if ( name.length() <= 46) { name += 'v';} else { name += 'f';} 55 if ( name[0] != 'i') { ;} else { name += 'z';} 56 if ( name.length() >= 38) { reverse(name.begin(),name.end());} else { name += 'b';} 57 cout<<name<<endl; 58 return 0; 59 }
T122398 Final Spark:
题意:拉克丝开大,发射一束宽度为w,长度无限的激光(方向随意)。提莫在距离她d(无用数据)的地方,提莫可视为一个直径为t的圆,他可以在她开大之前先往任意方向跑s的距离,问大招命中提莫的概率最大是多少。
分析:提莫最终的位置可以看成一个半径为s的圆,可以把提莫看成一个圆上的点,把宽度看成w+t(画个图便可推得),然后题目转化成一个矩形去切割圆问切到的弧长与圆的周长之比,求导(或观察)可得,相切时两者之比最大。

#include<bits/stdc++.h> using namespace std; const long double PI = acos(-1.0); int main(){ int T; scanf("%d",&T); while (T--){ double w,t,s,d; scanf("%lf%lf%lf%lf",&w,&t,&s,&d); if (w + t >= 2*s) printf("%lf ",1.000000000); else if (w+t == 0) printf("%lf ",0.000000000); else{ long double deg = acosl((s-w-t)/s); printf("%.9lf ",double(deg/PI)); } } return 0; }
T122399 Goldbach's conjecture:
题意:给一个偶数,求出它是哪两个素数的和。
分析:考虑到素数分布枚举即可,枚举方法可以加一些优化。

1 #include<bits/stdc++.h> 2 using namespace std; 3 bool isprime(int n){ 4 if(n==2||n==3) return 1; 5 if(n%6!=1&&n%6!=5) return 0; 6 for(int i=5;i<=floor(sqrt(n));i+=6) 7 if(n%i==0||n%(i+2)==0) return 0; 8 return 1; 9 } 10 int main(){ 11 int n; 12 scanf("%d",&n); 13 if (n == 4) puts("2 2"); 14 else { 15 if (isprime(n - 3)) cout << 3 << " " << n - 3 << endl; 16 else for (int i = 5, j = 2; ; i += j, j = j == 2 ? 4 : 2) { 17 if (isprime(i) && isprime(n - i)) { 18 cout << i << " " << n - i << endl; 19 break; 20 } 21 } 22 } 23 return 0; 24 }
T122400 Hazardous:
题意:给一个树,树上节点有相同或不同的颜色,问以每个编号为根的子树当中所有颜色相同的节点两两距离 的和。
分析:合并思想,合并一个根下面的两个节点,这个根的总值应加上它下面这两个节点的值以及合并这两个节点产生的贡献。
下面是推导题解产生贡献公式:
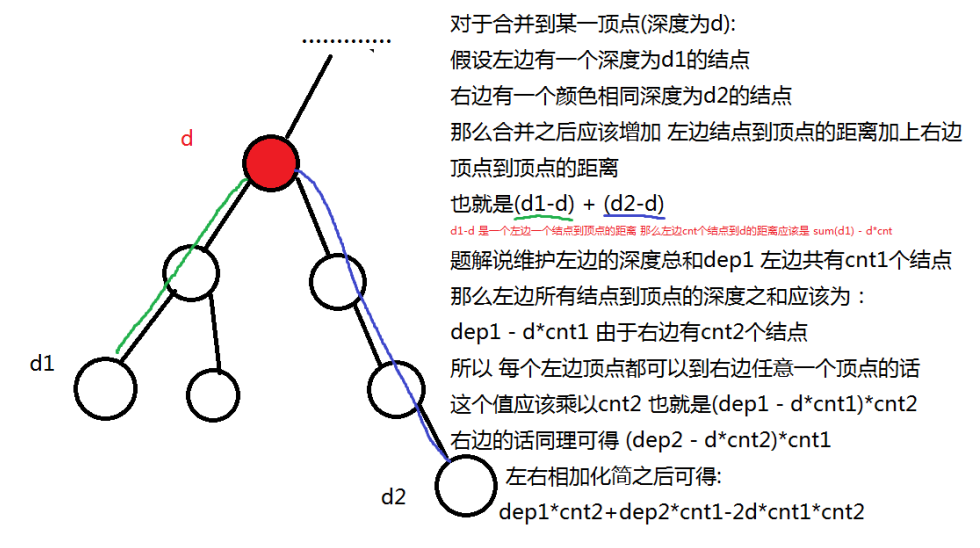
对于题解给的代码目前着实看不太懂,先放着吧有空再研究研究:
线段树版

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 typedef pair<int, int> pii; 5 6 #define N 201111 7 8 struct Node { 9 LL dep; 10 int l, r, cnt; 11 } t[N * 19]; 12 13 int n, tcnt; 14 int a[N], rt[N], dep[N]; 15 vector <int> E[N]; 16 LL sc[N], delta; 17 int curdep; 18 19 int Merge(int x, int y, int l, int r) { 20 if (!y) return x; 21 if (!x) return y; 22 if (l == r) { 23 delta += t[x].dep * t[y].cnt + t[y].dep * t[x].cnt - 2ll * curdep * t[x].cnt * t[y].cnt; 24 t[x].dep += t[y].dep; 25 t[x].cnt += t[y].cnt; 26 } 27 else { 28 int mid = (l + r) / 2; 29 t[x].l = Merge(t[x].l, t[y].l, l, mid); 30 t[x].r = Merge(t[x].r, t[y].r, mid + 1, r); 31 } 32 return x; 33 } 34 35 int init(int p, int l, int r) { 36 int x = ++tcnt; 37 if (l < r) { 38 int mid = (l + r) / 2; 39 if (p <= mid) t[x].l = init(p, l, mid); 40 else t[x].r = init(p, mid + 1, r); 41 } 42 else t[x].dep = curdep, t[x].cnt = 1; 43 return x; 44 } 45 void dfs(int x, int fa) { 46 curdep = dep[x];//记录当前节点的深度 curdep = current deep(当前节点深度)? 47 rt[x] = init(a[x], 1, n);// 48 for (int i = 0; i < E[x].size(); i++) {int v = E[x][i]; if (v != fa){//遍历当前节点的所有后继顶点 49 dep[v] = dep[x] + 1;//下一个节点的深度加一 50 dfs(v, x);//深搜下一节点 51 sc[x] += sc[v];//当前节点的ans等于他下面节点ans之和↓ 52 delta = 0;//初始化临时贡献 ↓ 53 curdep = dep[x];//更新当前深度 merge需要用到 ↓ 54 rt[x] = Merge(rt[x], rt[v], 1, n);// ↓ 55 sc[x] += delta;// 加上加入这个点后产生的贡献 ← 56 }} 57 } 58 59 int main() { 60 scanf("%d", &n); 61 for (int i = 1; i <= n; i++) scanf("%d", a + i); 62 for (int i = 1; i < n; i++) { 63 int u, v; 64 scanf("%d%d", &u, &v); 65 E[u].push_back(v); 66 E[v].push_back(u); 67 } 68 dfs(1, -1); 69 for (int i = 1; i <= n; i++) printf("%lld ", sc[i]); 70 }
map版

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 typedef pair<int, int> pii; 5 6 #define N 101111 7 8 int n; 9 int a[N], dep[N]; 10 11 typedef map <int, pair<long long, int>> Map; 12 Map rt[N]; 13 vector <int> E[N]; 14 LL sc[N], delta; 15 int curdep; 16 17 void Merge(Map &a, Map &b) { 18 if (a.size() < b.size()) swap(a, b); 19 for (auto& v : b) { 20 int col = v.first; 21 auto it = a.find(col); 22 if (it != a.end()) { 23 LL d1 = it->second.first, c1 = it->second.second; 24 LL d2 = v.second.first, c2 = v.second.second; 25 delta += d1 * c2 + d2 * c1 - 2ll * curdep * c1 * c2; 26 it->second.first += d2; 27 it->second.second += int(c2); 28 } 29 else { 30 a.insert(v); 31 } 32 } 33 } 34 35 void init(Map& r, int p) { 36 r[p] = {curdep, 1}; 37 } 38 39 void dfs(int x, int fa) { 40 curdep = dep[x]; 41 init(rt[x], a[x]); 42 for (auto v : E[x]) if (v != fa){ 43 dep[v] = dep[x] + 1; 44 dfs(v, x); 45 sc[x] += sc[v]; 46 delta = 0; 47 curdep = dep[x]; 48 Merge(rt[x], rt[v]); 49 sc[x] += delta; 50 } 51 } 52 53 int main() { 54 scanf("%d", &n); 55 for (int i = 1; i <= n; i++) scanf("%d", a + i); 56 for (int i = 1; i < n; i++) { 57 int u, v; 58 scanf("%d%d", &u, &v); 59 E[u].push_back(v); 60 E[v].push_back(u); 61 } 62 dfs(1, -1); 63 for (int i = 1; i <= n; i++) printf("%lld ", sc[i]); 64 }
附上原题&题解:


