1. 现在计算机中整数采用的编码方式:
A. 原码 B. 反码 C. Unicode 码 D. 补码
参考答案:D。
2. 下面程序的运行结果:
#include <iostream>
using namespace std;
void test(char c, char *d)
{
++c;
++*d;
cout << c << *d;
}
int main()
{
char a='A', b = 'a';
test(b, &a);
cout << a << b;
return 0;
}
A. BaBa B. aBaB C. AbAb D. bBAb
参考答案:D。test(b, &a),一个是传值,一个是传指针,后者在test函数中对其进行操作将改变其值。
3. 下面的说法那个正确:
#define NUMA 10000000
#define NUMB 1000
int a[NUMA], b[NUMB];
void pa()
{
int i, j;
for(i = 0; i < NUMB; ++i)
for(j = 0; j < NUMA; ++j)
++a[j];
}
void pb()
{
int i, j;
for(i = 0; i < NUMA; ++i)
for(j = 0; j < NUMB; ++j)
++b[j];
}
A. pa 和 pb 运行的一样快 B. pa 比 pb 快 C. pb 比 pa 快 D. 无法判断
参考答案:B。不确定
4. 10 个小球中只有一个红球,现在有放回地抽取一个小球,问至到第 n 次才取到 k 个红球 (k ≤ n) 的概率是多少 ?

参考答案:C。先求n-1次中取到k-1个红球的概率p,然后p乘以1/10的k次方,即为最终的概率。
5. 某指令流水线由 5 段组成,各段所需要的时间分别是:t、3t、t、2t 和 t 。问如果连续执行 10 条指令,则吞吐率是多少 ?
A. 0.1428/t B. 0.2041/t C. 0.2857/t D. 0.3333/t
参考答案:C。
解答:
第一条指令 -( ---)-(--)-
第二条指令 -(---)-(--)-
第三条指令 -(---)-(--)-
因为 是流水线,所以时间为3t的指令不能重叠,所以每隔3t时间开始一条指令,当第一条指令花费8t时间后,每隔3t完成一条指令,第10条指令完成的时间是:8+3*9=35t.
吞吐率为:10条指令/花费时间35t=10/35
弄懂两个概念就好做了:流水线时间和吞吐率 流水线时间计算有个公式:一条指令所需时间+(指令条数-1)*时间最长的指令的一段 // 8t+9*3t=35t 吞吐率也有个公式:指令条数除以流水线时间 // 10/35t
6. 现有两道四个选项的火星文单选题,你已经至少答对一题了,那么你两题都对的概率是多少 ?
A. 1/3 B. 1/4 C. 1/7 D. 1/8
参考答案:A。条件概率。A:两题都答对;B:至少答对一题,则P(A|B)=P(AB)/P(B)=(1/4)/(1-3/4)3/4)=1/3。
7. 以下是一个 tree 的遍历算法,queue 是一个 FIFO 队列。参考下面的 tree ,程序输出结果是神马。
queue.push(tree.root);
while(true){
node = queue.pop();
output(node.value); // 输出结点对应的数字
if(null = node)
break;
for(child_node in node.children){
queue.push(child_node);
}
}
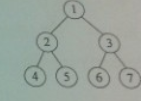
A. 1234567 B. 1245367 C. 1376254 D. 1327654
参考答案:A。
8. 堆排序的时间复杂度是多少 ? 堆排序建堆的时间复杂度是多少 ?
A. O(n2) O(n logn) B. O(n) O(nlogn) C. O(nlogn) O(n) D. O(nlogn) O(nlogn)
参考答案:C。堆排序的时间效率。建堆时间为O(n),之后有n-1次向下调整操作,每次调整的时间复杂度为O(h),所以在最好、最坏和平均情况下,堆排序的时间复杂度为O(nlog2(n))。
9. 字符串 "alibaba" 的二进制哈夫曼编码有多少位 ?
A. 11 B.12 C. 13 D. 14
参考答案:C。
10. 结点按中序遍历为 xyz 的二叉树有多少种可能 ?
A. 1 B.2 C.3 D.4 E. 5
参考答案:E。
11. 500 张纸牌整齐排成一排,按顺序编号 1、2、3、4、...、499、500,第一次拿走所有奇数位置上的纸牌,第二次再拿走剩下纸牌中的所有奇数位置上的纸牌,以此类推操作下去,问最后剩下的纸牌的编号是多少 ?
A. 128 B. 250 C. 256 D. 500
参考答案:C。
12. 一直矩阵 Ak = (aij)rk × rk+1,k = 1, 2, 3, 4, 5, 6 ;r1 = 5,r2 = 10,r3 = 3,r4 = 8,r5 = 5,r6 = 20,r7 = 6,问矩阵链乘 A1 × A2 × A3 × A4 × A5 × A6 的最佳求积次数是多少 ?
A. 2010 B. 2100 C. 2500 D. 2525
13. 有多少个 2012 位的数,这些数的任意两个相邻数位依序构成的两位数均能被 17 或 23 整除 ?
A. 3 B. 5. C. 7 D. 9
参考答案:B。

14. 关于 linux 的进程,下面说法不正确的是:
A. 僵尸进程会被 init 进程接管,不会造成资源浪费;
B. 孤儿进程的父进程在它之前退出,会被 init 进程接管,不会造成资源浪费;
C. 进程是资源管理的最小单位,而线程是程序执行的最小单位。Linux 下的线程本质上用进程实现;
D. 子进程如果对资源只是进行读操作,那么完全和父进程共享物理地址空间。
参考答案:A。
解析:A中孤儿进程会被init进程接管,而不是僵尸进程。详见http://www.cnblogs.com/Anker/p/3271773.html
15. 一个数据表有 10000 个元素,如果仅要求求出其中最大的 10 个元素,采用什么算法比较节省时间 ?
A. 堆排序 B. 希尔排序 C. 快速排序 D. 直接选择排序
参考答案:A。就是先取10个数,建一个堆,然后读后面的9990个数;每读一个数,跟堆里最小的数比较,如果比堆里最小的还小,就接着读;如果更大,则删除堆里最小的数,把新的数插入堆中,再接着读下一个数。直到所有数读完。
16. 一棵二叉树具有 8 个度为 2 的结点,5 个度为 1 的结点,则度为 0 的结点个数有多少个 ?
A. 6 B. 9 C. 11. D. 不确定
参考答案:B。N0=N2+1
17. 被除数是二进制数 110110,除数是二进制数 111,则余数是多少 ?
A. .100 B. 101 C. 110 D. 111
参考答案:B。
18. 对于下面的问题,不能使用栈 stack 来解决的是 ?
A. 数学表达式转换为后缀形式
B. 实现递归算法
C. 高级编程语言的过程调用
D. 操作系统分配资源(如 CPU)
参考答案:C。
19. 甲盒中有 200 个螺杆,其中有 160 个 A 型螺杆;乙盒中有 240 个螺母,其中有 180 个 A 型的。现从甲乙两盒中各任取一个,则能配成 A 型螺栓的概率为多少?
A. 1/20 B. 15/16 C. 3/5 D. 19/20
参考答案:C。
20. 有 A 和 B 两路公交车,平均发车时间间隔为 5 分钟和 10 分钟。某乘客在站点 S 可以任意选择两者之一乘坐,假定 A 和 B 到达 S 的时刻无法确定,那么该乘客的平均等待时间是多少 ?
A 1 分钟 20 秒 B. 1 分钟 40 秒 C. 2 分钟 30 秒 D. 3 分钟 20 秒
参考答案:D。
解析:在任意10分钟内,有两辆A路和一辆B路公交车经过S站,所以某乘客的平均等待时间为:10*60/3=200秒。
21. 下面不是引起进程调度原因的是 ?
A. 进程执行完毕 B. 进程 I/O 请求队列 C. 进程死循环 D. 进程调用阻塞原语进入睡眠状态
参考答案:C。进程死循环不是引起进程调度的原因。
22. 用于解决 CPU 指令乱序、编译器重排、多 CPU 内存同步等带来的问题的机制是 ?
A. 内存屏障 B. 信号量 C. 自旋锁 D. volatile 关键字
参考答案:ACD。这题不确定。信号量是为控制一个具有有限数量用户资源而设计,用于多线程并发范畴。
内存屏障:也称内存栅栏,内存栅障,屏障指令等, 是一类同步屏障指令,使得CPU或编译器在对内存随机访问的操作中的一个同步点,使得此点之前的所有读写操作都执行后才可以开始执行此点之后的操作。
自旋锁:自旋锁是专为防止多处理器并发而引入的一种锁,它在内核中大量应用于中断处理等部分(对于单处理器来说,防止中断处理中的并发可简单采用关闭中断的方式,即在标志寄存器中关闭/打开中断标志位,不需要自旋锁)。
volatile关键字:volatile提醒编译器它后面所定义的变量随时都有可能改变,因此编译后的程序每次需要存储或读取这个变量的时候,都会直接从变量地址中读取数据。如果没有volatile关键字,则编译器可能优化读取和存储,可能暂时使用寄存器中的值,如果这个变量由别的程序更新了的话,将出现不一致的现象。
23. 下面使用贪心算法的是:
A. 单元最短路径 Dijkstra 算法
B. 最小生成树 Prim 算法
C. 最小生成树 Kruskal 算法
D. 计算每对顶点最短路径的 Floyd-Warshall 算法
E. 字符串匹配中的 KMP 算法
参考答案:ABC。
解析:
分治法与动态规划的相同点:
分治法与动态规划,二者要求原问题具有最优子结构,都是将问题分而治之分解成若干个规模较小的子问题;
不同点:
1、动态规划是将原问题分解为多个子问题,通过计算出子问题的结果构造一个最优解。动态规划通过迭代法自底向上求解,动态规划将分解后的子问题理解为相互间有联系,有重叠的部分。其总是充分利用重叠子问题,即通过每个子问题只解一次,把解保存在一个表中,巧妙的避免了子问题的重复求解。
备忘录是动态规划的一个变种。采用的是自顶向下的思想,但是该方法维护了一个记录子问题解的表,虽然填表动作的控制结构更像递归方法,但是的确避免了子问题的重复求解。
算法的应用:装配线,矩阵乘法,最长公共子序列,构造最优的二叉树,最短路径(Floyd-Warshall)——求所有顶点之间的最短路径,0/1背包问题(不能选择物品的一部分,要么全拿,要么全不拿)。
2、分治法是将原问题分解为多个子问题,利用递归对各个子问题独立求解,最后利用各子问题的解进行合并形成原问题的解。分治法将分解后的子问题看成是相互独立的。
例如:在求解斐波那契数列过程中,求解fibonacci(5)求解fibonacci(5)时,得求解fibonacci(4)和fibonacci(3).其中,求解fibonacci(4)时,需要求解fibonacci(3).
在分治法中,求解完fibonacci(4)后还得重新求解fibonacci(3),即使求解fibonacci(4)子问题的时候已经求解过,也就是说,求解了二次子问题fibonacci(3).
3、贪心算法:依赖于当前已经做出的所有选择,采用自顶向下(每一步根据策略得到当前一个最优解,保证每一步都是选择当前最优的)的解决方法。
贪心算法的应用:最小生成树:普里姆(Prim)、克鲁斯卡尔(Kruskal),最短路径:迪杰斯特拉(Dijkstra)——求带全有向图中某个源点到其余各顶点的最短路径,数据压缩--哈夫曼编码,背包问题(可以选择物品的一部分)。
24. 关于 ACID 说法正确的是:
A. A 可用性。....
B. C 一致性。在食物开始之前和结束后,数据库的约束保持不变。
C. I 隔离性。两个同时运行的事务的执行是互不影响,中间结果不可交叉访问。
D. D 持久性。在事务提交之后,该事务所作的更改持久保存在存储介质之中,不会被回滚。
参考答案:BCD。A应该是原子性。
25. 现有一个循环队列,其队头指针为 front,队尾指针为 rear,循环队列的总长度为 N,问队内有效长度是多少 ?
参考答案:(rear-front)%N。
26. 一个数组 X,其中存有 N 个数字。现只允许遍历一遍,1) 有没有可能计算这些数字的方差 ? 2) 如果可以,请描述方案,如果不可以,说明原因。
思路:方差计算公式为:DX2 = E (X- EX) 2 这个公式是无法一次遍历就可求出方差的,需要遍历两次。
但方差公式还有个变形:DX2 = EX2- (EX) 2,利用这个公式即可以遍历一次求出方差。
详见:http://m.blog.csdn.net/blog/jxkongyue/11962439
27. 不使用临时变量交换 int a 和 int b 的值;请使用三行代码。
参考答案:a = a + b; b = a - b; a = a - b;
28. 下面的代码有一些问题,找出来:
#include <iostream>
using namespace std;
class Test{
public:
int *p;
Test(int v){
p = new int(v);
}
~Test(){
delete p;
}
void PrintValue(){
cout << "The value is " << *p << ' ';
}
};
void Func(Test t)
{
cout << "In the Func" << endl;
}
int main()
{
Test t1 = 33;//bug Test(33)
Func(t1);
t1.PrintValue();
}
29.Linux 平台,不提供任何相关库函数和工具包,只利用线程的随机调度特性和 sleep 函数的低精度特性,请编写一段程序实现:给一组字符,输出该组字符的一个随机化排列。
参考答案:http://m.blog.csdn.net/blog/u013140542/37918835。碰到这样的题目,顶多就写点思路了。
第四部分:JAVA选做题(注:阿里有大量JAVA研发工程师需求,选作一下题目有机会增加该方向面试机会)
1、请给出下面代码的输出
public class Test1 { public static int k = 0; public static Test1 t1 = new Test1("t1"); public static Test1 t2 = new Test1("t2"); public static int i = print("i"); public static int n = 99; public int j = print("j"); { print("构造块"); } static { print("静态块"); } public Test1(String str) { System.out.println((++k) + ":" + str + " i=" + i + " n=" + n); ++i; ++n; } private static int print(String str) { System.out.println((++k) + ":" + str + " i=" + i + " n=" + n); ++n; return ++i; } public static void main(String[] args) { Test1 t = new Test1("init"); } }
参考答案:
1:j i=0 n=0
2:构造块 i=1 n=1
3:t1 i=2 n=2
4:j i=3 n=3
5:构造块 i=4 n=4
6:t2 i=5 n=5
7:i i=6 n=6
8:静态块 i=7 n=99
9:j i=8 n=100
10:构造块 i=9 n=101
11:init i=10 n=102
解析:JAVA的类初始化顺序:(静态变量、静态初始化块)>(变量、初始化块)>构造器。且内部的初始化先后顺序为从上到下。

参考答案:不会。。。