hdu 4158 go! 队列+BFS

http://acm.hdu.edu.cn/showproblem.php?pid=4158

GO

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 205 Accepted Submission(s): 113

Problem Description

In the game of Go, two players alternate placing black and white stones on lattice points of an n × n grid, each attempting to surround as much territory (i.e., regions of unfilled lattice points) as possible. At the end of the game, the score for each player is the total area of the territory surrounded by his or her stones. Given the locations of black and white stones on a Go board at the end of a match, your task is to compute the score of each player in order to determine the winner.1
Formally, two grid lattice points with coordinates (r, c) and (r′, c′) are adjacent if |r - r′| + |c - c′| = 1. A connected region of unfilled lattice points belongs to one player’s territory if all adjacent filled lattice points contain stones belonging to that player (see Figure 1). Finally, a player’s score consists of the number of unfilled lattice points in his or her territory.

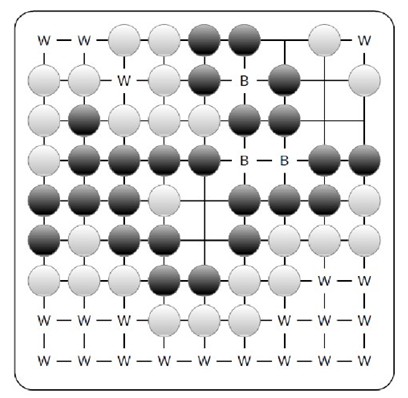
Note that the scoring of Go boards described here does not correspond exactly to the real game of Go: we make the simplifying assumptions that all “disputes” have been settled so that any territories surrounded by stones of both colors are considered neutral, and that all groups on the board are considered “alive.”

Figure 1: Diagram of a 9 × 9 Go board. Unfilled lattice points belonging to black’s territory are marked with B, and unfilled lattice points belonging to white’s territory are marked with W. Neutral unfilled lattice points are unmarked. In the game above, white wins by 21-3 = 18.

Input

The input test file will contain multiple cases, each consisting of three lines. Each test case begins with a line containing three integers, n (where 1 ≤ n ≤ 19), b, and w (where b ≥ 0,w ≥ 0 and 1 ≤ b + w ≤ n2). Here, n denotes the size of the board, b is the number of black pieces placed, and w is the number of white pieces placed. The second line of each test case contains b pairs of integers r1 c1 . . . rb cb (where 1 ≤ ri , ci ≤ n) indicating the positions of the b black stones. The third line of each test case contains w pairs of integers r`1 c`1 . . . r`w c`w (where 1 ≤ r`i , c`i ≤ n) indicating the positions of the w white stones. No two stones will be located at the same lattice point. Input is terminated by a single line containing only the number 0; do not process this line.

Output

For each test case, print either “White wins by ”, “Black wins by ”, or “Draw”.

Sample Input

1 0
1
0 1
1
12 4
1 1 2 1 3 2 1 2 3 3 1 3 3 4 1 4 3 5 1 5 2 5 3
4 2 4 3 4 3 5 
0

Sample Output

Draw
White wins by 3
Black wins by 1

Source

The 2011 Syrian Collegiate Programming Contest

Recommend

lcy

#include <stdio.h>
#include <queue>
using namespace std;


int map[20][20];
int nb,nw;
int n,b,w;
int d[4][2]={{1,0},{0,1},{-1,0},{0,-1}};

struct  Node
{
    int x,y;
}p,k;


void   bfs(int x,int y)
{
    int num=0;
    queue<Node> q;
    p.x=x;
    p.y=y;
    q.push(p);
    map[x][y]=3;
    int flag1=0,flag2=0;
    while(!q.empty())
    {
        k=q.front();
        q.pop();
        num++;
        for(int i=0;i<4;i++)
        {
            p.x=k.x+d[i][0];
            p.y=k.y+d[i][1];
            if(p.x>=1&&p.x<=n&&p.y>=1&&p.y<=n)
            {
                if(map[p.x][p.y]==0)
                {
                    q.push(p);
                    map[p.x][p.y]=3;
                }
                else if(map[p.x][p.y]==1)
                    flag1=1;
                else if(map[p.x][p.y]==2)
                    flag2=1;
            }
        }
    }
    if(flag1+flag2!=2)
    {
        if(flag1)
            nb+=num;
        if(flag2)
            nw+=num;
    }
}


int main()
{
    int x,y;
    int i,j;
    while(scanf("%d",&n)==1&&n)
    {
        scanf("%d%d",&b,&w);
        memset(map,0,sizeof(map));
        for( i=1;i<=b;i++)
        {
            scanf("%d%d",&x,&y);    //black
            map[x][y]=1;
        }
        for( i=1;i<=w;i++)
        {
            scanf("%d%d",&x,&y);    //white
            map[x][y]=2;
        }
        nb=nw=0;
        for( i=1;i<=n;i++)
          for( j=1;j<=n;j++)
            if(!map[i][j])
                bfs(i,j);
       if(nb==nw)
           printf("Draw\n");
       else if(nb-nw>0)
           printf("Black wins by %d\n",nb-nw);
       else if(nw-nb>0)
           printf("White wins by %d\n",nw-nb);

    }
  return 0;
}

queue队列容器-priority_queue优先队列

分类： ACM_STL 2010-02-22 10:02 718人阅读评论(0) 收藏举报

目录(?)[+]

关于队列的知识；

使用queue之前，要先利用构造函数一个队列对象，才可以进行元素的入队，出队，取队首和队尾等操作；

（1）.queue（） queue<int> q；或者 queue<int>Q[10000];

(2).queue(const queue&) 复制构造函数

例如：用一行代码利用queue对象q1，创建一个以双向链表为底层容器的queue对象q2

queue<int,list<int>>q1;

queue<int,list<int>>q2(q1);

(3).元素入队函数为：push（）例如：q.push(3),意思是将3入队 ,注意队列的大小不预设

（4）.元素出队函数为：pop（）例如：q.pop()

(5)。取对头元素函数为：front()

(6)，取队尾元素函数为：back()

(7)。判断对空函数为:empty()

(8)。队列的大小函数为：size（）返回队列的当前元素的个数

9.如何实现固定大小的queue队列

在每一次元素入队列前都判断当前的队列是否满，用双向链表做queue 的底层容器可以实现

优先队列基本上是一样的！只不过优先队列每一次队头元素都是队列中最大的元素！

取队头元素的函数为top（）

自动机

Time Limit:1s	Memory limit:32M
Accepted Submit:217	Total Submit:799

Tom博士最近研发了一个自动机，该自动机能够同时处理n个队列。其中，队列的编号为1..n。给定m个操作，模拟该自动机的工作状态。

第一行有2个整数n,m（1≤n, m≤10,000），表示自动机能处理n个队列，接下来m行每行一条操作指令。

每条指令的格式如下：

指令	指令说明
INIT	将自动机初始化，此时所有的队列清空。
PUSH id val	把整数val加入到编号id的队列的尾部。
POP id val	输出并删除编号id的队列的队首元素，如果队列为空，则输出“NULL”。

在每条指令中，id的编号在1..n中，val的取值范围为-2³¹~2³¹。输入数据保证操作的第一条指令都是是INIT。

数据输入输出

本题有多组输入数据，你必须处理到EOF为止。

请对输入数据中每条POP指令的结果依次输出一行结果。

输入样例

3 12 INIT PUSH 1 100 POP 2 PUSH 3 300 PUSH 1 200 PUSH 2 -5 POP 2 PUSH 2 -10 POP 1 INIT PUSH 1 7 POP 1

输出样例

NULL -5 100 7

问题解析:看到题目我们就应该知道这一题肯定是用队列解；联想到STL中的queue容器，】

关于队列的知识；

使用queue之前，要先利用构造函数一个队列对象，才可以进行元素的入队，出队，取队首和队尾等操作；

（1）.queue（） queue<int> q；或者 queue<int>Q[10000];

(2).queue(const queue&) 复制构造函数

例如：用一行代码利用queue对象q1，创建一个以双向链表为底层容器的queue对象q2

queue<int,list<int>>q1;

queue<int,list<int>>q2(q1);

(3).元素入队函数为：push（）例如：q.push(3),意思是将3入队 ,注意队列的大小不预设

（4）.元素出队函数为：pop（）例如：q.pop()

(5)。取对头元素函数为：front()

(6)，取队尾元素函数为：back()

(7)。判断对空函数为:empty()

(8)。队列的大小函数为：size（）返回队列的当前元素的个数

9.如何实现固定大小的queue队列

在每一次元素入队列前都判断当前的队列是否满，用双向链表做queue 的底层容器可以实现

例如：

#include<iostream>

#include<list>

#include<queue>

using namespace std;

#define QUEUE_SIZE 50 //固定大小为50

int main()

{

queue<int,list<int>> q;

if(q.size<QUEUE_SIZE)

q.push(51);

if(q.size<QUEUE_SIZE)

q.push(36);

if(q.size<QUEUE_SIZE)

q.push(28);

while(!q.empty())

{

cout<<q.front()<<endl; //打印51 36 28

q.pop(); //出队

}

return 0;

}

code:

#include<stdio.h>
#include<queue>
#include<string.h>
using namespace std;
int main()
{
register int i,j;
int m,n;
char c[6];
int x,y;
while(scanf("%d%d",&n,&m)!=EOF)
{
  queue<int>Q[10000];
  for(i=0;i<m;i++)
  {
   scanf("%s",&c);
   if(strcmp(c,"INIT")==0)
   {
    for(j=1;j<=n;j++)
    {
        while(!Q[j].empty())
     Q[j].pop();
    }
    continue;
   }
   if(strcmp(c,"PUSH")==0)
   { scanf("%d%d",&x,&y);
      Q[x].push(y);
       continue;
   }
   if(strcmp(c,"POP")==0)
   {
    scanf("%d",&y);
    if(Q[y].empty())
    {printf("NULL/n");continue;}
    else
     printf("%d/n",Q[y].front());
        Q[y].pop();
   }

}

}
return 0;
}

相关阅读:
Shell基础一
 Hash表
 哈希表
 设置不输入密码ssh登录
 C++ int与string的转化
 mysql之数据类型
 ICE之C/S通信原理
 mysql基础入门
 SQL练习之不反复执行相同的计算
 SQL练习之求解填字游戏
原文地址：https://www.cnblogs.com/hzg656343072/p/2692361.html