简介:
在算法的世界里,排序是最基本又是最重要的一类。在TACP(The Art of Computing Programming)中,占据了专门且重要的篇幅。在面试中也是屡屡出现。一般而言,排序是查找的基础,比如著名的二分查找,就是建立在有序序列的基础上的。
在众多的排序算法中,可以按照时间复杂度大概分为三类:
n平方阶的算法,
nlgn的算法(基于比较算法的下界)
线性时间的算法。
如果按排序的其他性质来分,又可以分为稳定排序/非稳定排序,等等。
知名的说法有常说的8大排序算法,专门指内部排序(与在磁盘上的外部排序相比,这些排序全部在内存中完成)。包括:
插入排序: 直接插入排序和希尔排序 12
选择排序: 简单选择排序和堆排序 34
交换排序: 冒泡排序和快速排序 56
归并排序 7
基数排序(是基于桶排序的) 8
1 O(n^2)
1.1 冒泡
基本思想:在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。每一趟排序后的效果都是讲没有沉下去的元素给沉下去。
算法流程:
1)比较相邻的两个元素,如果前面的数据大于后面的数据,就将两个数据进行交换;这样对数组第0个元素到第n-1个元素进行一次遍历后,最大的一个元素就沉到数组的第n-1个位置;
2)重复第2)操作,直到i=n-1。
时间复杂度分析:O(n^2),冒泡排序是一种不稳定排序算法。
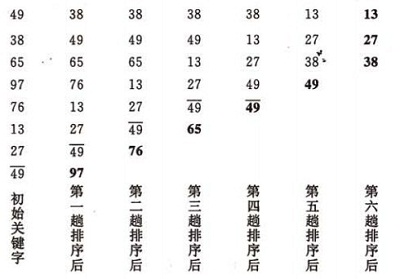
可以看到,冒泡排序跟选择排序有相似的地方,在经过一轮迭代以后,都是把最大元素排在最后。
冒泡排序的代码简单易懂,更适合作为教学目的之用。
2 O(nlogn)
归并(Merge)
是二分法的在排序算法中的一种典型应用。
快排
堆排
3 O(n)的算法
在CLRS一书中,四位作者已经证明了,对于基于比较的排序算法而言,它的下界就是O(nlgn),也就是说像归并之类的排序算法已经是最快了。但是如果打破基于比较去排序的这种思想藩篱,则其实还可以得到更快的排序算法:时间复杂度为线性的排序算法。
但是需要注意的是,这些算法的应用都有一些场景上的限制,即只有满足特定的条件,才能应用这些算法。。类似于快排一样的、通用的线性时间复杂度的排序算法是不存在的。
这类算法主要有:
桶排序
计数排序是桶排序的一种特殊情况,可以把计数排序当成每个桶里只有一个元素的情况。
桶排序要求数据的分布必须均匀,否则可能导致数据都集中到一个桶中。比如[104,150,123,132,20000], 这种数据会导致前4个数都集中到同一个桶中。导致桶排序失效。
网络各博文中流程的桶排序算法实际上都是计数排序,并非标准的桶排序。
基数
计数排序
它仅适用于数据比较集中的情况。比如 [0~100],[10000~19999] 这样的数据。
3.1 原理
计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前,应该有多少个元素来排序。针对数组arr,计算arr[i]之前有多少个元素,则唯一确定了arr[i]在排序后数组中的位置。
非比较排序只要确定每个元素之前的已有的元素个数即可,所有一次遍历即可解决。算法时间复杂度O(n)。
非比较排序时间复杂度底,但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。
参考文献
http://www.cnblogs.com/Leo_wl/p/4716681.html