工作证明与挖矿

工作证明

工作证明(Proof Of Work，简称POW)，顾名思义，即工作量的证明。通常来说只能从结果证明，因为监测工作过程通常是繁琐与低效的。

比特币在Block的生成过程中使用了POW机制，一个符合要求的Block Hash由N个前导零构成，零的个数取决于网络的难度值。要得到合理的Block Hash需要经过大量尝试计算，计算时间取决于机器的哈希运算速度。当某个节点提供出一个合理的Block Hash值，说明该节点确实经过了大量的尝试计算，当然，并不能得出计算次数的绝对值，因为寻找合理hash是一个概率事件。当节点拥有占全网n%的算力时，该节点即有n/100的概率找到Block Hash。

工作证明机制看似很神秘，其实在社会中的应用非常广泛。例如，毕业证、学位证等证书，就是工作证明，拥有证书即表明你在过去投入了学习与工作。生活大部分事情都是通过结果来判断的。

挖矿

挖矿即不断接入新的Block延续Block Chain的过程。

                                                                                     blockchain

挖矿为整个系统的运转提供原动力，是比特币的发动机，没有挖矿就没有比特币。挖矿有三个重要功能：

1. 发行新的货币（总量达到之前）
2. 维系货币的支付功能
3. 通过算力保障系统安全

金矿消耗资源将黄金注入流通经济，比特币通过“挖矿”完成相同的事情，只不过消耗的是CPU时间与电力。当然，比特币的挖矿意义远大于此。

Block Hash算法

Block头部信息的构成：

字段名	含义	大小(字节)
Version	版本号	4
hashPrevBlock	上一个block hash值	32
hashMerkleRoot	上一个block产生之后至新block生成此时间内， 交易数据打包形成的Hash	32
Time	Unix时间戳	4
Bits	目标值，即难度	4
Nonce	随机数	4

下面采用高度为125552的block数据为例，演示block hash的计算过程：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

<?php $header_hex = "01000000" . // version // previous block hash "81cd02ab7e569e8bcd9317e2fe99f2de44d49ab2b8851ba4a308000000000000" . // merkle root hash of transactions in this block "e320b6c2fffc8d750423db8b1eb942ae710e951ed797f7affc8892b0f1fc122b" . // Time "c7f5d74d" . // Bits (Difficulty) "f2b9441a" . // Nonce "42a14695"; $header_bin = pack("H*", $header_hex); // hex to bin $h = hash('sha256', hash('sha256', $header_bin, true), true); // double sha256 echo bin2hex($h), " "; // output: 1dbd981fe6985776b644b173a4d0385ddc1aa2a829688d1e0000000000000000 echo bin2hex(strrev($h)), " "; // output: 00000000000000001e8d6829a8a21adc5d38d0a473b144b6765798e61f98bd1d

该计算过程简单明了：首先将数个字段合并成一块数据，然后对这块数据进行双SHA256运算。

产量调节

Block的产量为大约每两周2016个，即每10分钟一块。该规则在每个节点的代码里都固定了。

1 2 3 4 5 6

// 目标时间窗口长度：两周 static const int64 nTargetTimespan = 14 * 24 * 60 * 60; // block频率，每10分钟一块 static const int64 nTargetSpacing = 10 * 60; // 每两周的产量2016，也是调节周期 static const int64 nInterval = nTargetTimespan / nTargetSpacing;

但由于实际算力总是不断变化的（目前一直是快速上升的），所以需根据最近2016个块的耗费时间来调整难度值，维持每10分钟一个block的频率.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

// Only change once per interval if ((pindexLast->nHeight+1) % nInterval != 0) { // 未达到周期个数，无需调节 return pindexLast->nBits; } // Go back by what we want to be 14 days worth of blocks const CBlockIndex* pindexFirst = pindexLast; for (int i = 0; pindexFirst && i < nInterval-1; i++) pindexFirst = pindexFirst->pprev; // 计算本次2016个块的实际产生时间 // Limit adjustment step int64 nActualTimespan = pindexLast->GetBlockTime() - pindexFirst->GetBlockTime(); // 限定幅度，最低为1/4，最高为4倍 if (nActualTimespan < nTargetTimespan/4) nActualTimespan = nTargetTimespan/4; if (nActualTimespan > nTargetTimespan*4) nActualTimespan = nTargetTimespan*4; // 根据最近2016个块的时间，重新计算目标难度 // Retarget CBigNum bnNew; bnNew.SetCompact(pindexLast->nBits); bnNew *= nActualTimespan; bnNew /= nTargetTimespan; if (bnNew > bnProofOfWorkLimit) bnNew = bnProofOfWorkLimit; return bnNew.GetCompact();

Block字段详解

• Version，版本号，很少变动，一般用于软件全网升级时做标识
• hashPrevBlock，前向Block Hash值，该字段强制多个Block之间形成链接
• hashMerkleRoot，交易Hash树的根节点Hash值，起校验作用，保障Block在网络传输过程中的数据一致性，有新交易加入即发生变化
• Time，Unix时间戳，每秒自增一，标记Block的生成时间，同时为block hash探寻引入一个频繁的变动因子
• Bits，可以推算出难度值，用于验证block hash难度是否达标
• Nonce，随机数，在上面数个字段都固定的情况下，不停地更换随机数来探寻

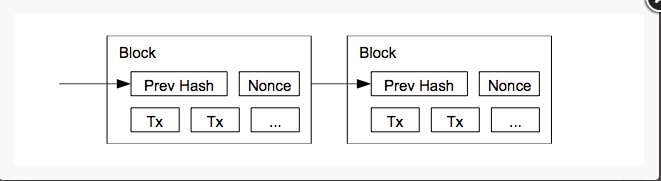
最为关键的字段是hashPrevBlock，该字段使得Block之间链接起来，形成一个巨大的“链条”。Block本是稀松平常的数据结构，但以链式结构组织起来后却使得它们具有非常深远的意义：

1. 形成分支博弈，使得算力总是在主分支上角逐
2. 算力攻击的概率难度呈指数上升（泊松分布）

每个block都必须指向前一个block，否则无法验证通过。追溯至源头，便是高度为零的创世纪块(Genesis Block)，这里是Block Chain的起点，其前向block hash为零，或者说为空。

新block诞生过程

下面是一个简单的步骤描述，实际矿池运作会有区别，复杂一些：

1. 节点监听全网交易，通过验证的交易进入节点的内存池(Tx Mem Pool)，并更新交易数据的Merkle Hash值
2. 更新时间戳
3. 尝试不同的随机数(Nonce)，进行hash计算
4. 重复该过程至找到合理的hash
5. 打包block：先装入block meta信息，然后是交易数据
6. 对外部广播出新block
7. 其他节点验证通过后，链接至Block Chain，主链高度加一，然后切换至新block后面挖矿

由于hashPrevBlock字段的存在，使得大家总是在最新的block后面开挖，稍后会分析原因。

主链分叉

从block hash算法我们知道，合理的block并不是唯一的，同一高度存在多个block的可能性。那么，当同一个高度出现多个时，主链即出现分叉(Fork)。遇到分叉时，网络会根据下列原则选举出Best Chain：

1. 不同高度的分支，总是接受最高（即最长）的那条分支
2. 相同高度的，接受难度最大的
3. 高度相同且难度一致的，接受时间最早的
4. 若所有均相同，则按照从网络接受的顺序
5. 等待Block Chain高度增一，则重新选择Best Chain

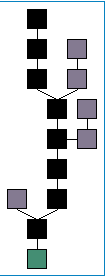
按照这个规则运作的节点，称为诚实节点(Honest Nodes)。节点可以诚实也可以不诚实。

分支博弈

我们假设所有的节点：

1. 都是理性的，追求收益最大化
2. 都是不诚实的，且不惜任何手段获取利益

所有节点均独自挖矿不理会其他节点，并将所得收益放入自己口袋，现象就是一个节点挖一个分支。由于机器的配置总是有差别的，那么算力最强的节点挖得的分支必然是最长的，如果一个节点的分支不是最长的，意味其收益存在不被认可的风险（即零收益）。为了降低、逃避此风险，一些节点肯定会联合起来一起挖某个分支，试图成为最长的分支或保持最长分支优势。

一旦出现有少量的节点联合，那么其他节点必然会效仿，否则他们收益为零的风险会更大。于是，分支迅速合并汇集，所有节点都会选择算力更强的分支，只有这样才能保持收益风险最小。最终，只会存在一个这样的分支，就是主干分支(Best/Main Chain)。

对于不诚实节点来说，结局是无奈的：能且只能加入主干挖矿。不加入即意味被抛弃，零收益；加入就是老实干活，按占比分成。

Hash Dance

Block hash的计算是随机概率事件，当有节点广播出难度更高的block后，大家便跑到那个分支。在比特币系统运行过程中，算力经常在分支间跳来跳去，此现象称为Hash Dance。一般情况下，分支的高度为1~2，没有大的故障很难出现高于2的分支。

Hash Dance起名源于Google Dance.

算力攻击的概率

本节内容参考：Bitcoin: A Peer-to-Peer Electronic Cash System

算力攻击是一个概率问题，这里作简单叙述：

• p = 诚实节点挖出block概率
• q = 攻击者挖出block概率，q = 1 - p
• qz = 攻击者从z个block追上的概率

                                                         算力攻击的概率

我们假设p>q，否则攻击者掌握了一半以上的算力，那么概率上永远是赢的。该事件（攻击者胜出）的概率是固定，且N次事件之间是相互独立的，那么这一系列随机过程符合泊松分布(Poisson Distribution)。Z个块时，攻击者胜出的期望为lambda：

攻击者胜出的期望

攻击者在攻击时已经偷偷的计算了k个块，那么这k个块概率符合泊松分布(下图左侧部分)，若k<=z，那么追赶上后续z-k个块的概率为(q/p)^(z-k)，即：

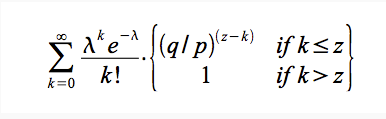
k个块概率符合泊松分布

展开为如下形式：

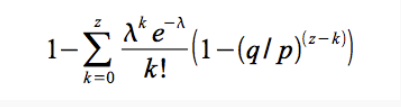
k个块概率符合泊松分布

计算该过程的C语言代码如下：

#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
    double sum    = 1.0;
    double p      = 1.0 - q;
    double lambda = z * (q / p);
    int i, k;
    for (k = 0; k <= z; k++) {
        double poisson = exp(-lambda);
        for (i = 1; i <= k; i++)
            poisson *= lambda / i;
        sum -= poisson * (1 - pow(q / p, z - k));
    }
    return sum;
}

我们选取几个值，结果如下：

                                                                                                 概率结果

可以看到，由于block的链式形式，随着块数的上升，攻击者赢得的概率呈指数下降。这是很多应用等待六个甚至六个以上确认的原因，一旦超过N个确认，攻击者得逞的可能微乎其微，概率值快速趋近零。

当攻击者的算力超过50%时，便可以控制Block Chain，俗称51%攻击。

算力攻击的危害

攻击者算出block后，block&Txs必须能够通过验证，否则其他节点都会拒掉，攻击便无意义。攻击者无法做出下列行为：

1. 偷盗他人的币。消费某个地址的币时，需要对应的ECDSA私钥签名，而私钥是无法破解的。
2. 凭空制造比特币。每个block奖励的币值是统一的规则，篡改奖励币值会导致其他节点会拒绝该block。

唯一的益处是可以选择性的收录进入block的交易，对自己的币进行多重消费(Double Spending)。

过程是这样的：假设现在block高度为100，攻击者给商户发了一个交易10BTC，记作交易A，通常这笔交易会被收录进高度101的block中，当商户在101块中看到这笔交易后，就把货物给了攻击者。此时，攻击者便开始构造另一个高度为101的block，但用交易B替换了交易A，交易B中的输入是同一笔，使得发给商户的那笔钱发给他自己。同时，攻击者需要努力计算block，使得他的分支能够赶上主分支，并合并(Merge)被大家接受，一旦接受，便成功地完成了一次Double Spending。

攻击难度呈指数上升，所以成功的Double Spending通常是一个极小概率事件。

算力巨头

全网算力的上升对比特币是极其有利的，这是毫无疑问的。但目前大矿池与矿业巨头使得算力高度集中化，这与中本聪所设想的一CPU一票（one-CPU-one-vote）的分散局面背道而驰，或许是他未曾预料的。

挖矿是一项专业劳动，最后必然会交给最专业的人或团队，因为这样才能实现资源配置最优，效率最高。普通投资人通过购买算力巨头的股票：1. 完成投资；2. 分享算力红利。看似中心化的背后其实依然是分散的：

1. 矿业公司的背后是无数分散的投资人
2. 矿池背后是无数分散的个体算力

既得利益使得算力巨头倾向于维护系统而不是破坏，因其收益均建立在比特币系统之上，既得利益者断然不会搬石头砸自己脚。甚至很多巨头在达到一定算力占比后会主动控制算力增长，使得低于某阈值内。

后记

本篇几乎都在讲挖矿，因为挖矿对于比特币系统来说实在是太重要了。需要了解：1. block是基于工作量证明的。2. block以链式结构存在时的深远意义。