运筹学那些事，专科学生学习运筹学之线性规划，No.4

文章目录

• 线性规划
• 概述
• 线性规划的模型结构
• 线性规划的图解法
• 求最大值问题
• 求最小值问题
• 单纯形法
• 一般最大值问题的求解法
• 套路总结
• 一般最小值问题的求解法
• 自考真题

线性规划

概述

重点概念提炼

• “规划” 就是使用某种数学方法使有效资源的运用达到最优化。
• 规划就是计算，以数学形式表达的一定条件下的一组方程式和/或一组不等式中求某些未知量。

线性规划的模型结构

线性规划的定义：线性规划是求一组变量的值，在满足一组约束条件下，求得目标函数的最优解，使决策目标达到最优，

线性规划模型的基本结构包含如下内容

1. 变量（也叫决策变量）
2. 目标函数（线性规划一般只解决单目标问题）
3. 约束条件
4. 线性规划的变量应为正值

线性规划建立模型时的四个步骤

1. 明确问题，确定目标，列出约束因素
2. 收集资料，确立模型
3. 模型求解与检验
4. 优化后分析

教材中提供了一个说明线性规划基本结构和建模基本步骤的案例

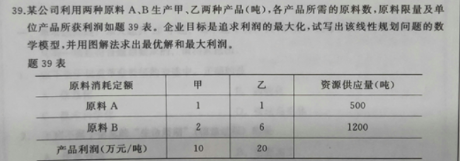
例题：设某家具厂生产桌子和碗橱两种产品，分别由加工、装配、油漆三个工段完成。相关数据如下

要求：在不超出三个工段的可用工时的情况下，合理搭配品种（桌子、碗橱），使得每班获得利润最大。

解答步骤：

（1）确定变量
设X₁为产品桌子产量，X₂为产品碗橱产量

（2）确定目标函数
桌子获得利润为8X₁，碗橱的利润为6X₁，故获得最大利润值的目标函数为：
极大值 S = 8X₁ + 6X₁

（3）列出约束条件
本案例中约束因素为三个工段的工时，其中加工工段为60小时，装配工段为48小时，油漆工段为36小时。
两个产品分别在不同工段所耗工时：加工工段为4X₁+2X₂，装配工段2X₁+4X₂，油漆工段2X₁+3X₂。
每个工段耗工时均不得超过计划期间内可利用的工时，故约束条件分别为：
加工工段 4X₁+2X₂ ≤ 60
装配工段 2X₁+4X₂ ≤ 48
油漆工段 2X₁+3X₂ ≤ 36

（4）变量的非负值 即 X₁，X₂ ≥ 0
因此，这个生产计划的线性规划模型为：

极大值 S = 8X₁ + 6X₁
满足于
4X₁+2X₂ ≤ 60
2X₁+4X₂ ≤ 48
2X₁+3X₂ ≤ 36
X₁，X₂ ≥ 0

线性规划的图解法

模型列出之后就需要求解。线性规划的基本解法有图解法（几何解法） 和 单纯解法 两种

求最大值问题

图解法分两步进行：

（1）求满足约束条件的可行解区

凡满足约束条件的解，均称之为可行解，可行解区就是全部可行解所分布的区域

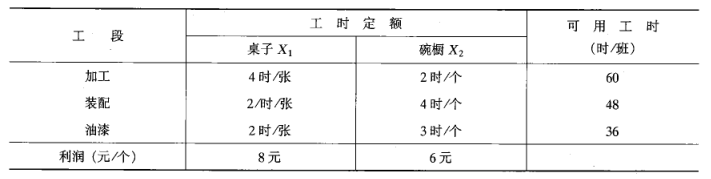
这个步骤其实非常简单，就是通过方程在坐标系中绘制，我截取一下教材上的一个图（本想自己绘制，发现软件不好找）

详细可以查阅教材第71页说明即可

绘制完毕图形之后，得到的域OCQB，就是线性规划模型的可行解区（凸集或叫可行域）。在这个区域内任何一点均满足所有约束条件的要求。

（2）从可行解区内，找满足目标函数的最优解

最优值的求得，就是从可行解区内找出一个合适的X₁，X₂值，使得目标函数的极值（如利润值）最大。

根据线性规划的基本原理认为：如果线性规划问题又最优解，就只可能在可行解区中的有限极点（角）上，最优的可行解避灾可行解区边缘折线的凸交点上。

教材第72页，也给出了相应的解答，比较容易理解，就不在赘述一遍了。

说白了，就是把目标函数画出来，然后画平行线，找到和哪个角重合，那个点如果距离原点O最远，就是满足目标函数方程极值（如利润值）最大的一个极点。

这个地方有几个比较关键的数学概念

作目标函数直线斜率相同的平行直线，这些直线称为等值线。

求最小值问题

设有某林场需配制某种灭虫药水500公斤，该药水系由甲与乙两种药水混合而成，甲种药水每公斤5元，乙种药水每公斤8元。按照两种药水的化学性质，在混合时，500公斤混合药水中含甲种药水最多不能超过400公斤，含乙种药水最少不能少于200公斤。

约束条件：

X ≤ 400
Y ≥ 200
X + Y = 500
X、Y ≥ 0

目标函数，求成本S的极小值：

S = 5X + 8Y

最小值的求解方法和最大值一致。翻看上述内容即可。

图解法用来解两个变量的线性规划问题是简单并且准确的。

单纯形法

单纯形法阶梯的基本步骤分为两步：

第一步 求一个基础可行解（可行基）
第二步 从求得的基础可行解出发，通过换基迭代，不断改进，得到最优解

一般最大值问题的求解法

教材中，给我们通过案例完整的解释了该种题目的解决办法，本篇博客重点提取一些关键部分进行说明

设某电视机厂生产两种电视机，彩色电视机和黑白电视机。这两种电视机的生产需要逐次经过两条装配线进行装配。其数据如表所示。为了使获得的利润最大，该厂每天应生产彩色电视机和黑白电视机各多少台？

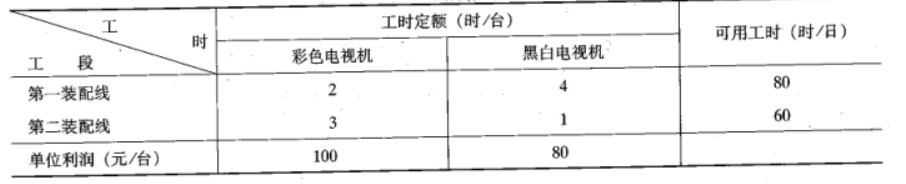
根据数据，设计模型如下，其中X₁，X₂分别表示彩色电视机与黑白电视机的台数

利润S的最大值：

S = 100X₁ + 80X₂
约束条件
2X₁ + 4X₂ ≤ 80
3X₁ + X₂ ≤ 60
X₁ + X₂ ≥ 0

解题步骤 该解题步骤，理论比较繁琐，耐心看完，可配合教材查阅，然后重点关注最后的答题技巧即可

1>>>>>>>>>> 以原点为基础可行解，建立初始方案，列出单纯形表
（1）引入辅助变量，将模型转换成标准形式。（这个辅助变量，在教材中定义为松弛变量）

现设下列松弛变量（以小时为单位）
K₁ 为装配线1的约束条件的松弛变量，表示装配线1 未被利用的工时
K₂ 为装配线2的约束条件的松弛变量，表示装配线2 未被利用的工时

2X₁ + 4X₂ + K₁ = 80 // 装配线1
3X₁ + X₂ + K₂ = 60 // 装配线2

由于K₁、K₂ 分别代表闲置工时，生产上不创造利润，所以它们在目标函数中的系数为0。即
100X₁ + 80X₂ + (0)K₁ + (0)K₂ = S
松弛变量的引入，不影响目标函数。所以，又称为辅助变量，主要用于辅助运算。

增加松弛变量后，得到如下的初始方案

100X₁ + 80X₂ + (0)K₁ + (0)K₂ = S
2X₁ + 4X₂ + K₁ = 80
3X₁ + X₂ + K₂ = 60
X₁ 、X₂、K₁、K₂ ≥ 0

注意，上述的松弛变量是正的。因为车间的约束条件是等于或者小于（≤）。但是，如果约束条件是大于或者等于（≥），那么将引进“剩余变量”，有时也称为负的松弛变量。

（2）列出单纯形表。以原点为基础，建立初始方案，即X₁= 0，X₂ = 0 将其代入模型，得

K₁ = 80 ， K₂ = 60，S = 0

显然，全部工时闲置，利润为0，方案不理想，调整改进。

为了便于运算，教材中采用的表格取代文字说明。由于填入的是以原点为基础的可行解的系数，故称之为初始单纯形表。

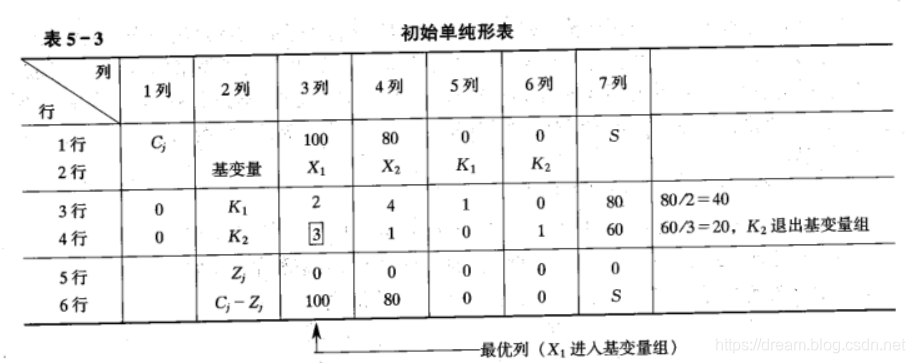
首先说明前面4行的含义

1. 第1行列出目标函数的系数
2. 第2行列出全部变量
3. 第3行、第4行列出两个约束方程的系数

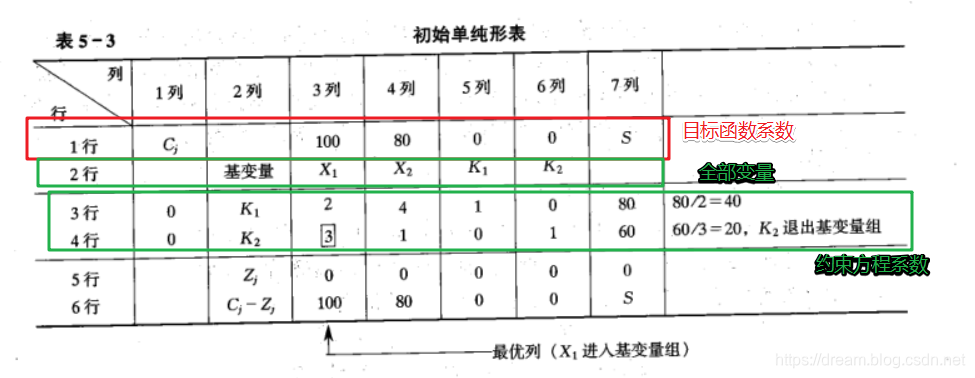
1. 第1列C_j 表示目标函数中的基变量K₁，K₂ 的系数；
2. 第2列为基变量
3. 第3列至第6列为对应于变量的系数（除第2行）
4. 第7列为常数列。约束条件右侧部分

单纯形表的后两行 - 第5行、第6行是用来确定 解是否还能得到改善。

看一下Z_j 行，它包括两部分

a. 常数列 （第7列）的Z_j值。表示基础可行解的利润值，或者说，表示未用时间K₁和K₂未做贡献，即没有生产产品X₁或X₂，也表示闲置时的损失值。它是常数列与C_j目标系数乘积之和，即
0*80+0*60 = 0

b. 变量X₁，X₂，K₁，K₂的Z_j值。它是所在列的系数与目标列系数C_j乘积之和。即

Z₁ = 0 * 2 + 0 * 3 = 0
Z₂ = 0 * 4 + 0 * 1 = 0
Z₃ = 0 * 1 + 0 * 0 = 0
Z₄ = 0 * 0 + 0 * 1 = 0

C_j - Z_j 行是单纯形表中的判别指数行。

在讨论线性规划问题的最优解 可行基解之前，我们先解释通解，特解，基解和可行基解 的含义

在线性规划中，设约束方程的个数为m,变量的个数为,m<n时，可把变量分别基变量和非基变量两部分，基变量个数为m个，非基变量个数为n-m个。基变量也可以叫基本变量或者基础变量，它可以用非基变量来表示，如上述案例，如果确定K₁，K₂为基变量时，它们就可以用非基变量X₁，X₂表示如下

K₁ = 80 - 2X₁ - 4X₂
K₂ = 60 - 3X₁ - X₂

这就是基变量组为K₁、K₂时，约束方程的通解。

根据变量非负的要求，我们给非基变量X₁，X₂ 一个具体的值，如X₁ = 10，X₂ = 5，则可得到K₁ = 40、K₂ = 25，这个就是一个特解，因为这个解满足约束方程组和变量非负的要求，所以是一个可行解（可以实行的解）

若令X₁ = 0 ，X₂ = 0 时，则得K₁ = 80，K₂ = 60，这也是一个特解，这个特解（0,0，80,60），因为所有的非基变量都等于0，所以叫做 基解 和 基础解。

一个基变量组只有一个通解、一个基解，有无穷个特解。

2>>>>>>>>>>进行第一次迭代
（1）基变量、非基变量的转变。首先从初始表开始，用最高的正直选择列。
首先选出X₁ 为基变量（因为100大于80，生产1个单位的X₁价值大）

选定X₁之后，需要把原来的K₁、K₂中的一个转换成非基变量。转变的原则是 根据变量非负的原则。

如何决定使K₁还是K₂转换为非基变量呢？教材中提供的办法是查找 常数项/X₁ 的系数 这一比值最小的一个。

80/2 和 60/3 这些比值中最小的一个，然后把这个最小值所对应的原基变量转变为非基变量。该题中将K₂转变为非基变量

这时在下图所示的第3列，第4行所相交的那一格的数字3上画一个方格,表示这是一个交换格。

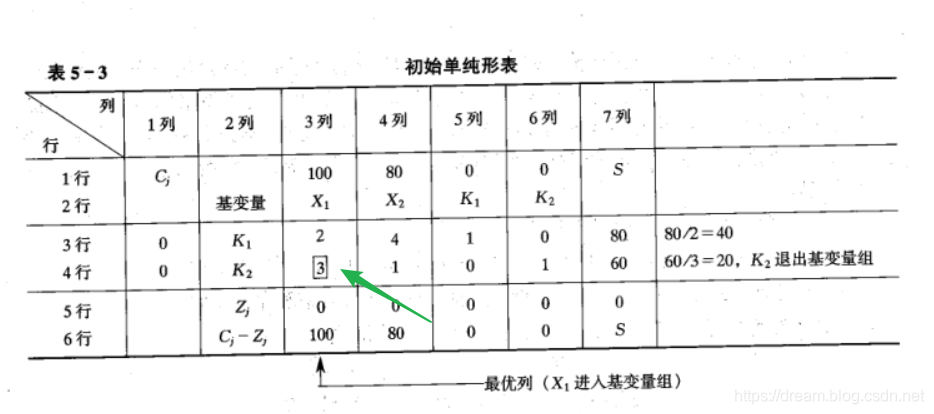
如何保证K₁在基变量组转变为（K₁，X₁）后，在新的基解中非负就是接下来要研究的问题了

若此基变量组（K₁，X₁）有最优解的话，一定是一个可行基解，即非基变量（X₂,K₂）全为0，基变量（K₁，X₁）都≥0，因此考察K₁的正负，只要看常数项即可。

1/2K₁ = 80/2 - 60/3。

因为60/3 是几个比值中最小的比值，所以，1/2K₁ = 80/2 - 60/3 必然大于或等于0。

这就证明了，当X₁的通解 代入 1/3K₁ 的通解，以消去X₁时，基变量 K₁ 的常数项非负，从而保证了K₁在新的基解中非负。

接下来就是迭代过程了，这个过程是你需要掌握的

第一次迭代

表1

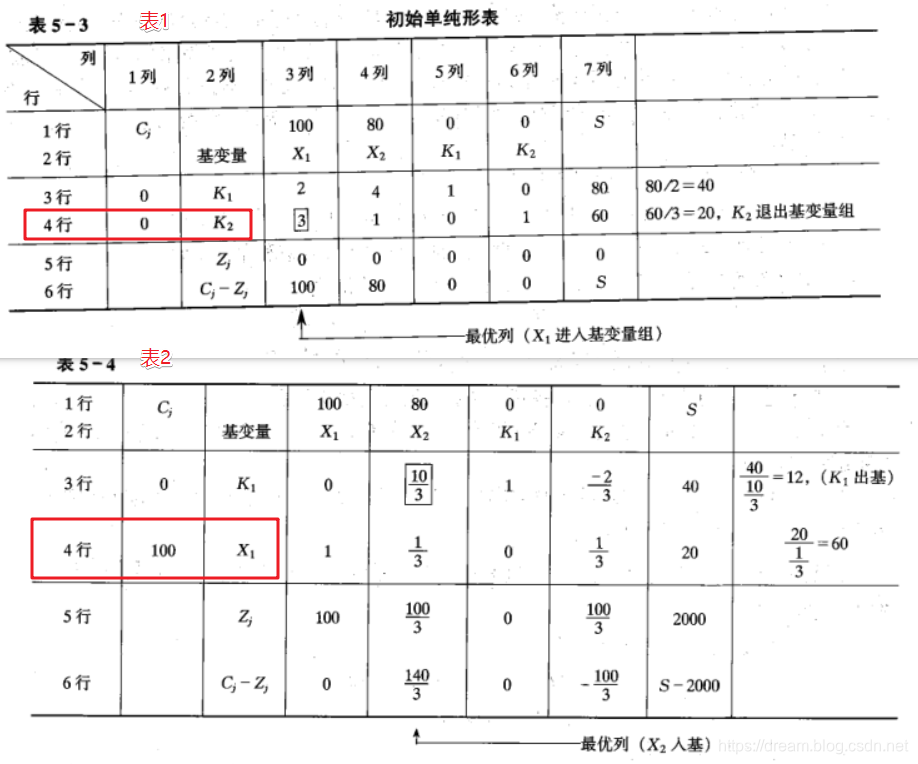
第（1）步：把表1中第4行C_j列下的0换成100（即新的基变量X₁在目标函数中的系数），把K₂换成X₁。所以第4行应变成X₁的通解，我们用X₁的系数3除表1的第4行

X₁ + 1/3 X₂ + 1/3 K₂ = 20

第（2）步：通过表2，新的第4行与表1第3行，构成的方程组，做差去掉X₁
表1的第3行：2X₁ + 4X₂ + K₁ = 80
表2的第4行*2：2X₁ + 2/3 X₂ + 2/3 K₂ = 40

上面的两个式子相减
0 +10/3 X₂ + K₁ - 2/3K₂ = 40，这个就是表2的第3行

Z_j行：
先回忆一下目标函数 S = 100X₁ + 80X₂

为了在目标函数中消去X₁,所以用目标函数中X₁的系数100，乘以表2第4行，得到表2的第5行

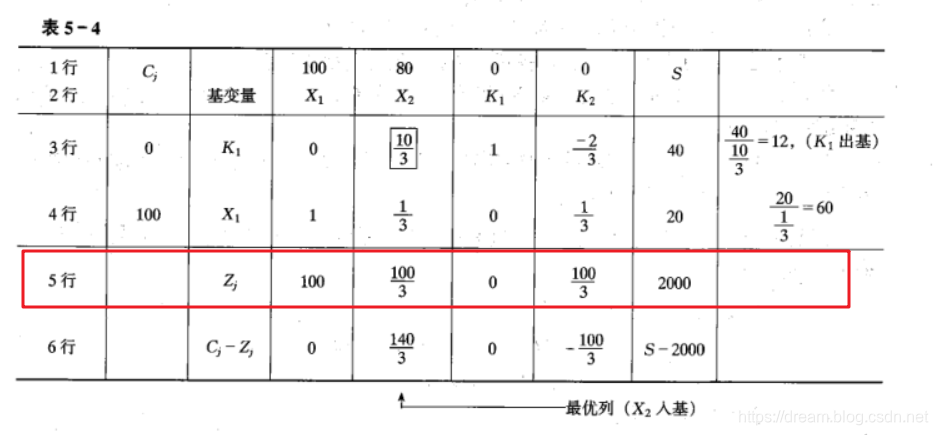
C_j - Z_j行：表2的第1行减去Z_j行，得新的由非基变量X₂，K₂表示的目标函数。

S-2000 = 140/3 X₂ -100/3 K₂

max S = 2000 + 140/3 X₂ - 100/3 K₂

目标函数中，X₂的系数>0，这表示如果给X₂正数值，利润还可以增加，因此就需要第二次迭代。

第二次迭代
（1）基变量、非基变量的转变。
在表2的C_j - Z_j行中，只有X₂的系数>0，所以选择X₂为新的基变量，那么原来的K₁和X₁哪一个转变成非基变量呢？

查看X₂的系数，发现各行中X₂的系数与常数项同为整数。然后查找 常数项/X₂的系数 这一比值最小的一个，发现 40/(10/3) = 12，20/(1/3) = 60 ，前者小，因此确定K₁转变为非基变量（出基）

第二次迭代在下面的两个表中进行

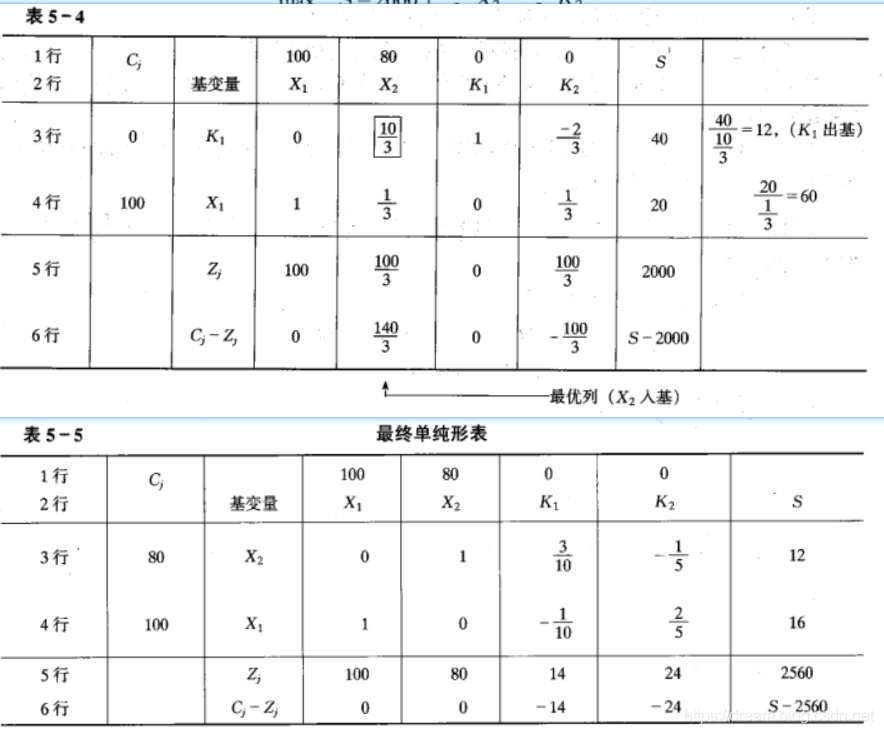
1. 首先把表5-4的第1行的目标函数写入表5-5的第1行。
2. 在确定X₂为新的基变量以后，用表5-4第3行X₂的系数10/3除该行，求出X₂的通解
   X₂ = 12-3/10K₁ + 1/5K₂
3. 经过移项，写入表5-5第3行
4. X₂已变为基变量，在将表5-4第4行移入表5-5时应消去X₂
5. 表5-4第4行：X₁+1/3X₂+1/3K₂ = 20
6. 表5-5第3行乘以1/3：1/3X₂+1/10K₁-1/15K₂ = 4
7. 表5-4第4行与上式相减，得：X₁-1/10K₁+2/5K₂ = 16

为了消去表5-5的X₁，X₂，以第3行X80，第4行X100，然后两行相加，得
100X₁ + 80X₂ + 14K₁ - 24K₂ = 2560

第C_j - Z_j 行，为非基变量K₁，K₂ 表示的新目标函数。它实际上就是以表5-5中X₁，X₂的通解带入初始目标函数后，所得的结果

S = 100X₁ + 80 X₂

S = 2560 - 14K₁ - 24K₂

从这个目标函数中可以看到，K₁、K₂ 的系数全为负数，因此我们若给K₁、K₂以正数值，只能使利润下降，只有当我们给K₁、K₂以零值时，才能获得利润的最大值。

因此当K₁ = 0、K₂ = 0 时，X₁（彩色电视机） = 16，X₂ （黑白电视机） = 12 ，S = 2560
（16,12,0，0）就是我们所求的最优可行解，于此对应的最大利润为2560。

套路总结

一般最大值问题的单纯形法，初步看上去，很复杂，其实套路非常简单

第一步：初始单纯形表

第一行，放目标函数形参
第二行，放未知数
第三行，放约束条件的参数（基变量）
第四行，放约束条件的参数（基变量）

第一列，放基变量的系数
第二列，放基变量，Z~j~,C~j~ - Z~j~
第三列~第六列，对应变量的系数
第七列，放常数列

第二步：把单位提高一个，利润提高多的那个变量(假设是X₁)转变为基变量，然后将原基变量转变为非基变量(假设值K₂)
这个地方，找常数项/X₁ 的系数比较小的，即可。
找到之后，在表格中标记出来

第三步：X₁变为基变量之后，需要把表格中的指定行，修改为X₁的参数。因为X₁是基变量，所以包含X₁的式子，需要调整，调整方法，就是用新表新的一行乘以一个倍数，去减原表的那行。（其实说白了，就是方程组中的消除元的方法）

第四步：Z_j 这行目的就是消去基变量，注意核对C_j行数字即可

重复上述步骤迭代即可，最终必须将原基变量的值置为0才可以。

加强练习

一般最小值问题的求解法

最小值的解题步骤相对于最大值问题的求解法，难度系数更大一些，该部分内容，想要学习的可以自行研究一下，因为在自考或者期末考试中出现的概率比较低，故不在延展。

自考真题

注意，线性规划属于自考中非常重要的一个章节，在自考中一般以压轴题目出现（就是最难的，出现在最后的一道题目）

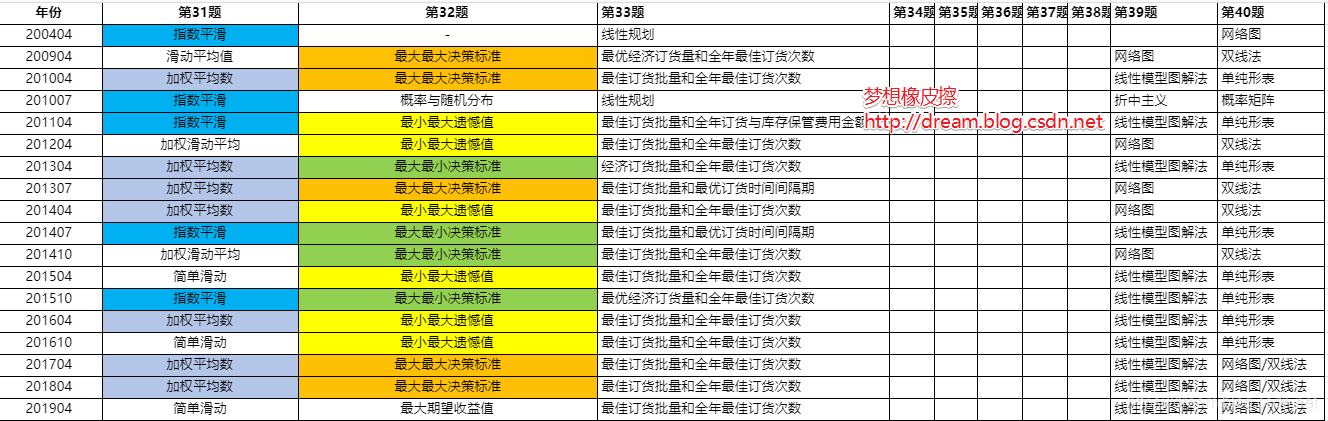
注意看，前些年第39题和第40题每次都是在网络图+双线法，图解法+单纯形表转换，近3年已经调整为两部分都需要考察，可以预测2020年之后，可能会采用相同的策略。

更多内容，欢迎关注 https://dwz.cn/r4lCXEuL

附录2019年4月考题：