运筹学那些事，专科学生学习运筹学之马尔柯夫分析，No.8

文章目录

• 马尔柯夫分析的数学原理
• 概率向量
• 概率矩阵
• 定理1
• 定理2
• 定理3
• 马尔柯夫分析问题的要求
• 品牌转换实例分析说明
• 导出转移概率矩阵
• 未来市场份额的预测
• 确定平衡条件
• 市场份额与平衡状态的关系
• 马尔柯夫分析在管理工作中的应用
• 自考说明

马尔柯夫分析的数学原理

在某些事物的概率转换过程中，第n次试验的结果，常常由第n-1次试验的结果所决定

马尔柯夫过程：对于由一种情况转换至另外一种情况的过程，若该过程具有转换概率，而且此种转换概率又可以依据其紧接的前项情况推算出来，则这种过程即称为马尔柯夫过程。

一连串的此种转换过程的整体称为马尔柯夫锁链。

对于马尔柯夫过程或马尔柯夫锁链可能产生之演变加以分析，以观察和预测该过程或该锁链未来变动的趋向，则这种分析、观察和预测的工作即为马尔柯夫分析。

概率向量

任意一个向量 μ = (μ₁，μ₂，μ₃，…，μ_n)，如果它内部的各个元素非负数，且总和等于1，则此向量称为概率向量。如 μ = (0.25,0.25,0.5) 即为概率向量

概率矩阵

一方阵 P = (P_ij) 中，如果其各行都是概率向量，则此方阵称为概率矩阵或概率方阵。

定理1

如果A和B都是概率矩阵，则AB的乘积亦为概率矩阵，同理Aⁿ亦为概率矩阵。

定理2

设有概率矩阵

即Pⁿ矩阵中的每一个行向量都相等。Pⁿ称作P的固定概率矩阵或平衡概率矩阵。证明属于数学上的内容，有兴趣的了解，教材中给的是一些案例

由于对矩阵内的概率值只取两位小数（对经济管理问题已经足够用），因此上述两幅图中，上图到P⁸已得到平衡概率矩阵，下图到P⁶已经趋向平衡。

定理3

设有任一概率向量T = （t₁，t₂，…，t_n），任一概率矩阵

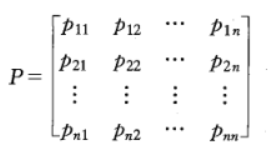
当n->∞时，必有：TPⁿ = (z₁，z₂，…，z_n)，其中向量Z = (z₁，z₂，…，z_n) 为固定概率矩阵Pⁿ中的任一行向量。

马尔柯夫分析问题的要求

马尔柯夫分析的定义为：通过分析几种变量现时运动的情况来预计这些量未来运动情况的一种方法。

或者说，马尔柯夫分析是分析某变量的当前状况并预测该变量未来状况的一种方法。

品牌转换实例分析说明

假设某居民小区的牛奶全部由A、B、C三个牛奶场供应。每个牛奶场都知道，由于宣传广告、服务不周或其他原因，订户在一段时间内常发生从一家牛奶场订转向另一家牛奶场订奶的情况。如果三家牛奶场都保存着他们的订户数和和每户饮用哪家牛奶场牛奶的记录，我们就具备了应用这个企业管理工具所具备的一切资料。

假定表9-1说明在一个月的观察期内订户的流动情况。为了进一步简化必需的数字，我们假定在此期间，既没有老订户退出，也没有新订户加入

粗略一看，会以为在一个月中有20个订户转了户：10个从B转向A，10个从C转向A。该结论错误，需要从更加细致的角度分析。参照下表- 订户之间的真实转换。从下图可以看到，牛奶场A增添20个订户是三个牛奶场订户复杂的移动结果。这种活动在销售学上有时叫做商标转换

本部分比较容易，直接看教材即可，最终的结论如下

按净得或净失订户所做的简单分析对精明的管理是不合适的。对从各个对口获得的比率和损失给各个对手的比率，管理部分所需要的是更细致的分析。

有上述这些数据，管理人员可以：

1，预测未来某个时刻各销售者在市场中得到的份额。
2，预测将来销售者在市场中份额的得失比率。
3，预测将来会不会出现市场平衡（稳定或拉平市场份额）。
4，按照对市场份额得失的确切效果来分析销售者的推销活动。

为了将上述简单例子过渡到马尔柯夫分析，我们计算三个牛奶场的转移概率。转移概率就是某个销售者（本例为牛奶场）保持、获得或失去消费者的概率。

说白了就是牛奶场B失去了50个订户，也就是它保持订户的概率是0.9，牛奶场A保持订户的概率是0.8，牛奶场C保持订户的概率是0.85

从上图中，已经对每个牛奶场每月保持老订户的比例，有所了解了。接下来要计算其他概率。下表是获取到的数据，不是计算得来的。（销售中采集到的数据）

导出转移概率矩阵

接下来将上述9-3表和9-4表转换成更精确的形式，其中各种增益或者损失全部换算成转移概率。转移概率排列成一种叫做矩阵的格式（矩阵是线性代数中的概念）

根据表9-3和9-4得到如下转移概率矩阵

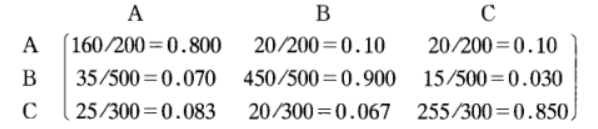
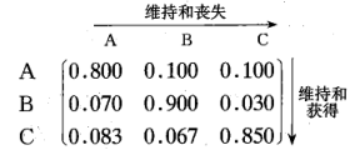
经过计算之后转移矩阵为

通过转移概率的矩阵各行可以做出一些理解
以下内容直接照搬教材内容，了解即可

第一行指出牛奶场A保持其0.8的订户（160户），丧失0.1的订户（20户）给牛奶场B，丧失0.1的订户（20户）给牛奶场C
第二行指出牛奶场B保持其0.9的订户（450户），丧失0.07的订户（35户）给牛奶场A，丧失0.03的订户（15户）给牛奶场C
第三行指出牛奶场C保持其0.85的订户（255户），丧失0.083的订户（25户）给牛奶场A，丧失0.067的订户（20户）给牛奶场B

逐列观察得出下列信息：

第一列指出牛奶场A保持其0.8的订户（160户），获得牛奶场B的0.07的订户（35户），获得牛奶场C的0.083的订户（25户）。
第二列指出牛奶场B保持其0.9的订户（450户），获得牛奶场A的0.1的订户（20户），获得牛奶场C的0.067的订户（20户）。
第三列指出牛奶场C保持其0.85的订户（255户），获得牛奶场A的0.1的订户（20户），获得牛奶场B的0.03的订户（15户）。

有了这样的信息，基本关系就能较容易地考察到。
用矩阵显示数据对市场管理产生多种好处。它可根据市场分享率的增加和减少帮助管理者分析其努力的效果。它可以预测一种牌号的市场分享率在将来增加或减少的速率，而且可以看出将来市场平衡的可能性。

未来市场份额的预测

7月1日的市场份额分别为 A = 22% ，B = 49%，C = 29%

如果想要计算牛奶场在8月1日可能占整个市场多少份额，只需要把7月1日的市场份额排成一个矩阵，并把这个矩阵与转移概率的矩阵相乘。（线性代数的基础知识）

所以 8月1日可能的市场份额为：
（0.234，0.483，0.283） 总和 = 1.000

9月1日的市场份额

计算方法一：

将8月1日的可能市场份额乘以原转移概率矩阵

计算方法二：

用7月1日的市场份额乘以原转移概率矩阵的平方

计算方式属于数学基础内容，手动计算比较麻烦，一般由计算机负责计算

确定平衡条件

三个最终的即平衡的市场份额是什么

1. 独家牛奶场的平衡
   为说明平衡，新设一个转移概率的矩阵：
   
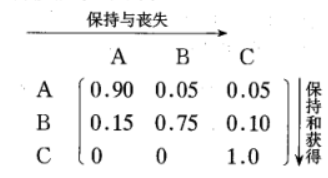
   因为C从来不丧失一个订户，而其它牛奶场不断地把订户丧失给C，因此C迟早会拥有所有的用户。用马尔柯夫的术语来说，这叫做一个单状态的槽或盆，意思是牛奶场之一的C最终获得全部订户，C也叫做一个吸收状态。

2. 两个牛奶场的平衡
   第二类平衡也能出现
   
   该图不太对，下图更合适一些
   
   很容易看出，牛奶场B和牛奶场C最终夺走了A的所有订户，B与C最终评分市场。这叫做一个双槽或盆

3. 三个牛奶场的平衡

该平衡不存在槽和盆的平衡

确定平衡条件，篇幅不大，了解即可

市场份额与平衡状态的关系

最终的平衡状态取决于转移概率不变，而与初始市场份额无关

马尔柯夫分析在管理工作中的应用

1. 在设备修理中的应用
2. 选择设备保养地点
3. 选择零件的更换方式
4. 预测人口的变动情况
5. 预测市场占有率

自考说明

更多内容，欢迎关注 https://dwz.cn/r4lCXEuL

对于马尔柯夫分析法相关知识在自考中占比比例不高，但是具备很大的应用价值，尤其是本章结尾前的马尔柯夫分析在管理工作中的应用，大家可以更加深入的了解一下

从2017年~2019年，近三年都出现了相关试题，考察内容以未来市场份额预测为主，请重点掌握！！！