合集地址
二叉树合集(一):二叉树基础(含四种遍历,图文详解)
二叉树合集(二):霍夫曼树(图文详解)
二叉树合集(三):线索二叉树(图文详解)
二叉树合集(四):对称二叉树(递归和迭代实现)
二叉树合集(五):二叉搜索树(图片详解,含基本操作)
二叉树合集(六):高度平衡二叉树
前言
树是数据结构中的重中之重,尤其以各类二叉树为学习的难点。一直以来,对于树的掌握都是模棱两可的状态,现在希望通过写一个关于二叉树的专题系列。在学习与总结的同时更加深入的了解掌握二叉树。本系列文章将着重介绍一般二叉树、完全二叉树、满二叉树、线索二叉树、霍夫曼树、二叉排序树、平衡二叉树、红黑树、B树。希望各位读者能够关注专题,并给出相应意见,通过系列的学习做到心中有“树”。
1 重点概念
1.1 结点概念
结点是数据结构中的基础,是构成复杂数据结构的基本组成单位。
1.2 树结点声明
本系列文章中提及的结点专指树的结点。例如:结点A在图中表示为:
树
2.1 定义
**树(Tree)**是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:
1)有且仅有一个特定的称为根(Root)的结点;
2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、…、Tn,其中每一个集合本身又是一棵树,并且称为根的子树。
此外,树的定义还需要强调以下两点:
1)n>0时根结点是唯一的,不可能存在多个根结点,数据结构中的树只能有一个根结点。
2)m>0时,子树的个数没有限制,但它们一定是互不相交的。
示例树:
图2.1为一棵普通的树:
由树的定义可以看出,树的定义使用了递归的方式。递归在树的学习过程中起着重要作用,
2.2 结点的度
结点拥有的子树数目称为结点的度。
图2.2中标注了图2.1所示树的各个结点的度。
2.3 结点关系
结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。
图2.2中,A为B的双亲结点,B为A的孩子结点。
同一个双亲结点的孩子结点之间互称兄弟结点。
图2.2中,结点B与结点C互为兄弟结点。
2.4 结点层次
从根开始定义起,根为第一层,根的孩子为第二层,以此类推。
图2.3表示了图2.1所示树的层次关系
2.5 树的深度
树中结点的最大层次数称为树的深度或高度。图2.1所示树的深度为4。
3 二叉树
3.1 定义
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
图3.1展示了一棵普通二叉树:
3.2 二叉树特点
由二叉树定义以及图示分析得出二叉树有以下特点:
1)每个结点最多有两颗子树,所以二叉树中不存在度大于2的结点。
2)左子树和右子树是有顺序的,次序不能任意颠倒。
3)即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。
3.3 二叉树性质
1)在二叉树的第i层上最多有2i-1 个节点 。(i>=1)
2)二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1)
3)n0=n2+1 n0表示度数为0的节点数,n2表示度数为2的节点数。
4)在完全二叉树中,具有n个节点的完全二叉树的深度为[log2n]+1,其中[log2n]是向下取整。
5)若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号,则对完全二叉树中任意一个编号为 i 的结点有如下特性:
(1) 若 i=1,则该结点是二叉树的根,无双亲, 否则,编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n,则该结点无左孩子, 否则,编号为 2i 的结点为其左孩子结点;
(3) 若 2i+1>n,则该结点无右孩子结点, 否则,编号为2i+1 的结点为其右孩子结点。
3.4 斜树
斜树:所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。
3.5 满二叉树
满二叉树:在一棵二叉树中。如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
满二叉树的特点有:
1)叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
2)非叶子结点的度一定是2。
3)在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
3.6 完全二叉树
完全二叉树:对一颗具有n个结点的二叉树按层编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
图3.5展示一棵完全二叉树
特点:
1)叶子结点只能出现在最下层和次下层。
2)最下层的叶子结点集中在树的左部。
3)倒数第二层若存在叶子结点,一定在右部连续位置。
4)如果结点度为1,则该结点只有左孩子,即没有右子树。
5)同样结点数目的二叉树,完全二叉树深度最小。
注:满二叉树一定是完全二叉树,但反过来不一定成立。
3.7 二叉树的存储结构
3.7.1 顺序存储
二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点,并且结点的存储位置,就是数组的下标索引。
图3.6
图3.6所示的一棵完全二叉树采用顺序存储方式,如图3.7表示:
由图3.7可以看出,当二叉树为完全二叉树时,结点数刚好填满数组。
那么当二叉树不为完全二叉树时,采用顺序存储形式如何呢?例如:对于图3.8描述的二叉树:
其中浅色结点表示结点不存在。那么图3.8所示的二叉树的顺序存储结构如图3.9所示:
其中,∧表示数组中此位置没有存储结点。此时可以发现,顺序存储结构中已经出现了空间浪费的情况。
那么对于图3.3所示的右斜树极端情况对应的顺序存储结构如图3.10所示:
由图3.10可以看出,对于这种右斜树极端情况,采用顺序存储的方式是十分浪费空间的。因此,顺序存储一般适用于完全二叉树。
3.7.2 二叉链表
既然顺序存储不能满足二叉树的存储需求,那么考虑采用链式存储。由二叉树定义可知,二叉树的每个结点最多有两个孩子。因此,可以将结点数据结构定义为一个数据和两个指针域。表示方式如图3.11所示:
定义结点代码:
typedef struct BiTNode{
TElemType data;//数据
struct BiTNode *lchild, *rchild;//左右孩子指针
} BiTNode, *BiTree;
则图3.6所示的二叉树可以采用图3.12表示。
图3.12中采用一种链表结构存储二叉树,这种链表称为二叉链表。
3.8 二叉树遍历
二叉树的遍历一个重点考查的知识点。
递归解法
递归解法是比较常用而且容易理解的方法,只要理解了思路就能够很好的去使用他。
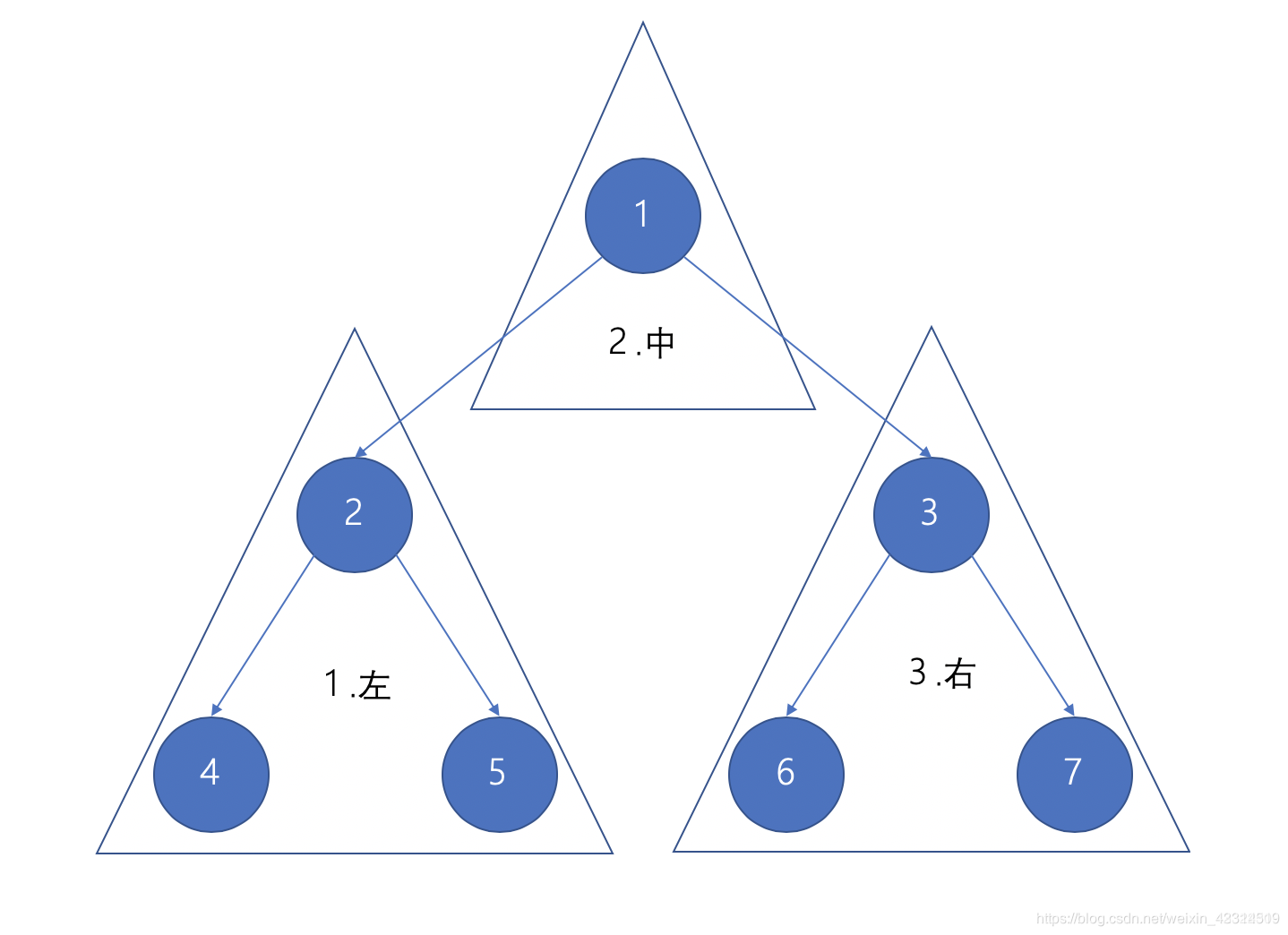
**比如前序遍历:**前序遍历的递归方法就是:根、左、右,先打印根节点,只有再去寻找他的左子树,左子树找到末尾的时候返回再找又指数,直到完成。
下面放代码:
前序遍历
public static void PreOrderRecur(TreeNode root){
if(root == null) return;
System.out.println(root.data);
PreorderRecur(root.left);
PreorderRecur(root.right);
}
中序遍历
public static void InOrderRecur(TreeNode root){
if(root == null) return;
InorderRecur(root.left);
System.out.println(root.data);
InorderRecur(root.right);
}
后序遍历
public static void PostOrderRecur(TreeNode root){
if(root == null) return;
PostorderRecur(root.left);
PostorderRecur(root.right);
System.out.println(root.data);
}
观察可以发现,递归的实现其实只是输出根节点的位置不一样,并没有很大的不同。
迭代解法
本质上是在模拟递归,因为在递归的过程中使用了系统栈,所以在迭代的解法中常用Stack来模拟系统栈。注意栈的先进后出顺序,输出出来的就是倒序打印。
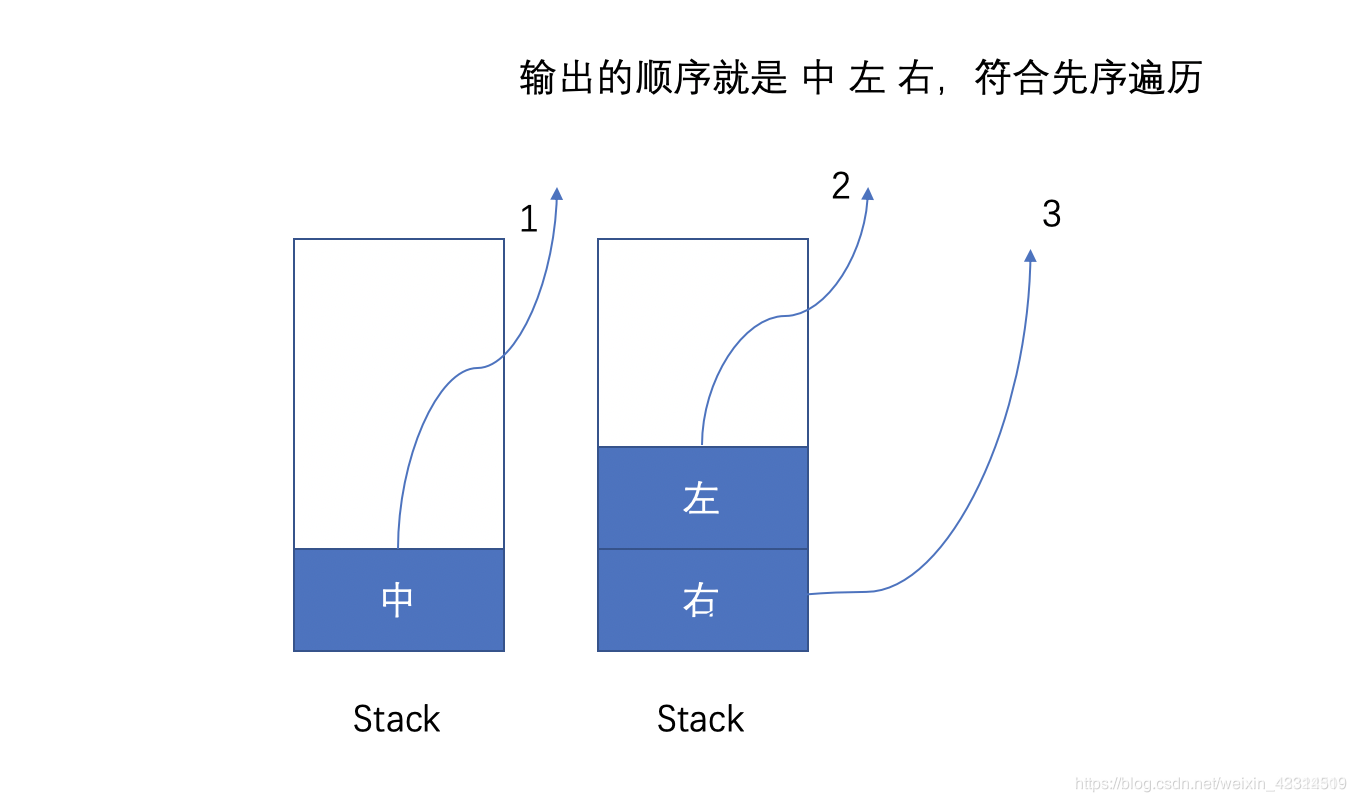
前序遍历
⼆叉树的前序遍历顺序是根-左-右。我们可以采⽤⼀个栈来辅助,我们把先序遍历的结果放到⼀个ArrayList 容器中作为返回值,具体步骤如下:
1、把⼆叉树的根节点 root 放进栈。
2、如果栈不为空,从栈中取出⼀个节点,把该节点放⼊容器的尾部;如果该节点的右⼦树不为空,则
把有节点放⼊栈;如果该节点的左⼦树不为空,则把左⼦树放⼊栈中。
3、⼀直重复步骤 2 ,直到栈为空,此时遍历结束,代码如下:
static List<Interger> PreOrderTraversal(TreeNode root){
List(Interger) result = new ArrayList<>();
Stack<TreeNode> stack = new Stack();
if(root == null) return result;
stack.push(root);//首先把根节点放入栈中
while(!stack.isEmpty(){
//当栈中不为空的时候,执行以下操作
TreeNode temp = stack.pop();//取出栈中的节点,用一个临时变量保存
result.add(temp.val);//将变量的值加入结果队列中
if(tmp.right!=null)
stack.push(root.right);//如果该节点的右⼦树不为空,则把有节点放⼊栈
if(tmp.left!=null)
stack.push(root.left);//如果该节点的左⼦树不为空,则把左⼦树放⼊栈中。
}
return result;
}
中序遍历
⼆叉树的中序遍历顺序是左-根-右。我们可以采⽤⼀个栈来辅助,我们把中序遍历的结果放到⼀个
ArrayList 容器中作为返回值,具体步骤如下:
1、进⼊ while 循环,接着把根节点及其所有左⼦节点放⼊栈中。
2、从栈中取出⼀个节点,把该节点放⼊容器的尾部;如果该节点的右⼦节点不为空,则把右⼦节点及
其右⼦节点的所有左⼦节点放⼊队列。
3、⼀直重复步骤 2 ,直到栈为空并且当前节点也为空则退出循环。
可能看解释反⽽有点乱,直接看代码吧,配合代码就容易懂了
代码如下:
public List<Integer> InOrderTraversal(TreeNode root){
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
while (root != null || !stack.isEmpty())
{
if(root != null){
stack.push(root);
root=root.left;
}
else{
root = stack.pop();
res.add(root.data);
root=root.right;
}
}
return res;
}
后续遍历
宽搜+逆序输出 = 后序遍历
⼆叉树的后序遍历顺序是左-右-根。我们可以采⽤⼀个栈来辅助,不过它和前序遍历以及中序遍历还是有点区别的,我们把后序遍历的结果放到⼀个 LinkedList 容器中作为返回值,具体步骤如下:
1、把⼆叉树的根节点 root 放进栈。
2、如果栈不为空,从栈中取出⼀个节点,把该节点插⼊到容器的头部。;如果该节点的左⼦树不为
空,则把该左⼦树放⼊栈中;如果该节点的右⼦树不为空,则把右⼦树放⼊栈中。,
注意,之前的前序遍历和中序遍历,我们都是⽤ ArrayList 容器,并且是把节点插⼊到容器的尾部,这
就是后序遍历的不同点。
3、⼀直重复步骤 2 ,直到栈为空,此时遍历结束
代码如下:
public List<Integer> postOderTraversal(TreeNode root) {
LinkedList<Integer> res = new LinkedList<>();// 注意,采⽤链表
Stack<TreeNode> stack = new Stack<>();
if(root == null)
return res;
stack.push(root);
while (!stack.isEmpty()) {
TreeNode tmp = stack.pop();// 注意,是放在第⼀个位置
res.addFirst(tmp.val);
if(tmp.left != null)
stack.push(tmp.left);
if(tmp.right != null)
stack.push(tmp.right);
}
return res;
}
层序遍历
请参考我的另一篇博文,链接。
4 结语
通过上述的介绍,已经对于二叉树有了初步的认识。本篇文章介绍的基础知识希望读者能够牢牢掌握,并且能够在脑海中建立一棵二叉树的模型,为后续学习打好基础。