欢迎关注WX公众号:【程序员管小亮】
【机器学习】《机器学习》周志华西瓜书 笔记/习题答案 总目录
——————————————————————————————————————————————————————
习题

这个题在南瓜书中证明过了,我们也在笔记中写过了,笔记链接——《机器学习》周志华西瓜书学习笔记(八):集成学习



这个题也在南瓜书中证明过了,我们也在笔记中写过了,笔记链接——《机器学习》周志华西瓜书学习笔记(八):集成学习

这意味着 达到了贝叶斯最优错误率,即若指数损失函数最小化,则分类错误率也将最小化。这说明指数损失函数是分类任务原本的0 / 1 损失函数的 一致的(consistent)替代损失函数。由于这个替代函数有更好的数学性质,例如它是连续可微函数,因此用它替代0 / 1 损失函数作为优化目标。

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
class Node(object):
def __init__(self):
self.feature_index = None
self.split_point = None
self.deep = None
self.left_tree = None
self.right_tree = None
self.leaf_class = None
def gini(y, D):
'''
计算样本集y下的加权基尼指数
:param y: 数据样本标签
:param D: 样本权重
:return: 加权后的基尼指数
'''
unique_class = np.unique(y)
total_weight = np.sum(D)
gini = 1
for c in unique_class:
gini -= (np.sum(D[y == c]) / total_weight) ** 2
return gini
def calcMinGiniIndex(a, y, D):
'''
计算特征a下样本集y的的基尼指数
:param a: 单一特征值
:param y: 数据样本标签
:param D: 样本权重
:return:
'''
feature = np.sort(a)
total_weight = np.sum(D)
split_points = [(feature[i] + feature[i + 1]) / 2 for i in range(feature.shape[0] - 1)]
min_gini = float('inf')
min_gini_point = None
for i in split_points:
yv1 = y[a <= i]
yv2 = y[a > i]
Dv1 = D[a <= i]
Dv2 = D[a > i]
gini_tmp = (np.sum(Dv1) * gini(yv1, Dv1) + np.sum(Dv2) * gini(yv2, Dv2)) / total_weight
if gini_tmp < min_gini:
min_gini = gini_tmp
min_gini_point = i
return min_gini, min_gini_point
def chooseFeatureToSplit(X, y, D):
'''
:param X:
:param y:
:param D:
:return: 特征索引, 分割点
'''
gini0, split_point0 = calcMinGiniIndex(X[:, 0], y, D)
gini1, split_point1 = calcMinGiniIndex(X[:, 1], y, D)
if gini0 > gini1:
return 1, split_point1
else:
return 0, split_point0
def createSingleTree(X, y, D, deep=0):
'''
这里以C4.5 作为基学习器,限定深度为2,使用基尼指数作为划分点,基尼指数的计算会基于样本权重,
不确定这样的做法是否正确,但在西瓜书p87, 4.4节中, 处理缺失值时, 其计算信息增益的方式是将样本权重考虑在内的,
这里就参考处理缺失值时的方法。
:param X: 训练集特征
:param y: 训练集标签
:param D: 训练样本权重
:param deep: 树的深度
:return:
'''
node = Node()
node.deep = deep
if (deep == 2) | (X.shape[0] <= 2): # 当前分支下,样本数量小于等于2 或者 深度达到2时,直接设置为也节点
pos_weight = np.sum(D[y == 1])
neg_weight = np.sum(D[y == -1])
if pos_weight > neg_weight:
node.leaf_class = 1
else:
node.leaf_class = -1
return node
feature_index, split_point = chooseFeatureToSplit(X, y, D)
node.feature_index = feature_index
node.split_point = split_point
left = X[:, feature_index] <= split_point
right = X[:, feature_index] > split_point
node.left_tree = createSingleTree(X[left, :], y[left], D[left], deep + 1)
node.right_tree = createSingleTree(X[right, :], y[right], D[right], deep + 1)
return node
def predictSingle(tree, x):
'''
基于基学习器,预测单个样本
:param tree:
:param x:
:return:
'''
if tree.leaf_class is not None:
return tree.leaf_class
if x[tree.feature_index] > tree.split_point:
return predictSingle(tree.right_tree, x)
else:
return predictSingle(tree.left_tree, x)
def predictBase(tree, X):
'''
基于基学习器预测所有样本
:param tree:
:param X:
:return:
'''
result = []
for i in range(X.shape[0]):
result.append(predictSingle(tree, X[i, :]))
return np.array(result)
def adaBoostTrain(X, y, tree_num=20):
'''
以深度为2的决策树作为基学习器,训练adaBoost
:param X:
:param y:
:param tree_num:
:return:
'''
D = np.ones(y.shape) / y.shape # 初始化权重
trees = [] # 所有基学习器
a = [] # 基学习器对应权重
agg_est = np.zeros(y.shape)
for _ in range(tree_num):
tree = createSingleTree(X, y, D)
hx = predictBase(tree, X)
err_rate = np.sum(D[hx != y])
at = np.log((1 - err_rate) / max(err_rate, 1e-16)) / 2
agg_est += at * hx
trees.append(tree)
a.append(at)
if (err_rate > 0.5) | (err_rate == 0): # 错误率大于0.5 或者 错误率为0时,则直接停止
break
# 更新每个样本权重
err_index = np.ones(y.shape)
err_index[hx == y] = -1
D = D * np.exp(err_index * at)
D = D / np.sum(D)
return trees, a, agg_est
def adaBoostPredict(X, trees, a):
agg_est = np.zeros((X.shape[0],))
for tree, am in zip(trees, a):
agg_est += am * predictBase(tree, X)
result = np.ones((X.shape[0],))
result[agg_est < 0] = -1
return result.astype(int)
def pltAdaBoostDecisionBound(X_, y_, trees, a):
pos = y_ == 1
neg = y_ == -1
x_tmp = np.linspace(0, 1, 600)
y_tmp = np.linspace(-0.2, 0.7, 600)
X_tmp, Y_tmp = np.meshgrid(x_tmp, y_tmp)
Z_ = adaBoostPredict(np.c_[X_tmp.ravel(), Y_tmp.ravel()], trees, a).reshape(X_tmp.shape)
plt.contour(X_tmp, Y_tmp, Z_, [0], colors='orange', linewidths=1)
plt.scatter(X_[pos, 0], X_[pos, 1], label='1', color='c')
plt.scatter(X_[neg, 0], X_[neg, 1], label='0', color='lightcoral')
plt.legend()
plt.show()
if __name__ == "__main__":
data_path = r'..datawatermelon3_0a_Ch.txt'
data = pd.read_table(data_path, delimiter=' ')
X = data.iloc[:, :2].values
y = data.iloc[:, 2].values
y[y == 0] = -1
trees, a, agg_est = adaBoostTrain(X, y)
pltAdaBoostDecisionBound(X, y, trees, a)


这个问题,网上已经有很多总结了:
Gradient Boosting和其它Boosting算法一样,通过将表现一般的数个模型(通常是深度固定的决策树)组合在一起来集成一个表现较好的模型。抽象地说,模型的训练过程是对一任意可导目标函数的优化过程。通过反复地选择一个指向负梯度方向的函数,该算法可被看做在函数空间里对目标函数进行优化。
因此可以说Gradient Boosting = Gradient Descent + Boosting。
和AdaBoost一样,Gradient Boosting也是重复选择一个表现一般的模型并且每次基于先前模型的表现进行调整。不同的是,AdaBoost是通过提升错分数据点的权重来定位模型的不足,而Gradient Boosting是通过算梯度(gradient)来定位模型的不足。因此相比AdaBoost,Gradient Boosting可以使用更多种类的目标函数。

代码如下:
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.utils import resample
def stumpClassify(X, dim, thresh_val, thresh_inequal):
ret_array = np.ones((X.shape[0], 1))
if thresh_inequal == 'lt':
ret_array[X[:, dim] <= thresh_val] = -1
else:
ret_array[X[:, dim] > thresh_val] = -1
return ret_array
def buildStump(X, y):
m, n = X.shape
best_stump = {}
min_error = 1
for dim in range(n):
x_min = np.min(X[:, dim])
x_max = np.max(X[:, dim])
# 这里第一次尝试使用排序后的点作为分割点,效果很差,因为那样会错过一些更好的分割点;
# 所以后来切割点改成将最大值和最小值之间分割成20等份。
# sorted_x = np.sort(X[:, dim])
# split_points = [(sorted_x[i] + sorted_x[i + 1]) / 2 for i in range(m - 1)]
split_points = [(x_max - x_min) / 20 * i + x_min for i in range(20)]
for inequal in ['lt', 'gt']:
for thresh_val in split_points:
ret_array = stumpClassify(X, dim, thresh_val, inequal)
error = np.mean(ret_array != y)
if error < min_error:
best_stump['dim'] = dim
best_stump['thresh'] = thresh_val
best_stump['inequal'] = inequal
best_stump['error'] = error
min_error = error
return best_stump
def stumpBagging(X, y, nums=20):
stumps = []
seed = 16
for _ in range(nums):
X_, y_ = resample(X, y, random_state=seed) # sklearn 中自带的实现自助采样的方法
seed += 1
stumps.append(buildStump(X_, y_))
return stumps
def stumpPredict(X, stumps):
ret_arrays = np.ones((X.shape[0], len(stumps)))
for i, stump in enumerate(stumps):
ret_arrays[:, [i]] = stumpClassify(X, stump['dim'], stump['thresh'], stump['inequal'])
return np.sign(np.sum(ret_arrays, axis=1))
def pltStumpBaggingDecisionBound(X_, y_, stumps):
pos = y_ == 1
neg = y_ == -1
x_tmp = np.linspace(0, 1, 600)
y_tmp = np.linspace(-0.1, 0.7, 600)
X_tmp, Y_tmp = np.meshgrid(x_tmp, y_tmp)
Z_ = stumpPredict(np.c_[X_tmp.ravel(), Y_tmp.ravel()], stumps).reshape(X_tmp.shape)
plt.contour(X_tmp, Y_tmp, Z_, [0], colors='orange', linewidths=1)
plt.scatter(X_[pos, 0], X_[pos, 1], label='1', color='c')
plt.scatter(X_[neg, 0], X_[neg, 1], label='0', color='lightcoral')
plt.legend()
plt.show()
if __name__ == "__main__":
data_path = r'..datawatermelon3_0a_Ch.txt'
data = pd.read_table(data_path, delimiter=' ')
X = data.iloc[:, :2].values
y = data.iloc[:, 2].values
y[y == 0] = -1
stumps = stumpBagging(X, y, 21)
print(np.mean(stumpPredict(X, stumps) == y))
pltStumpBaggingDecisionBound(X, y, stumps)
以决策树桩作为Bagging的基学习器,效果不太好。尝试了下,设置基学习器数量为21时算是拟合最好的,决策边界如下:


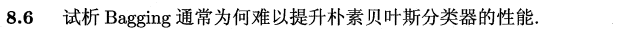
书中P177和P179提到过:
从偏差—方差分解的角度看, Boosting 主要关住降低偏差,因此 Boosting 能基于泛化性能相当弱的学习器构建出很强的集成.
从偏差—方差分解的角度看, Bagging 主要关注降低方差,因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显.
在统计学习框架下,大家刻画模型复杂度的时候,有这么个观点,认为 Error = Bias + Variance。这里的Error大概可以理解为模型的预测错误率,是有两部分组成的,一部分是由于模型太简单而带来的估计不准确的部分(Bias),另一部分是由于模型太复杂而带来的更大的变化空间和不确定性(Variance)。
方差大(偏差低)的模型往往是因为对训练数据拟合得过好,模型比较复杂,输入数据的一点点变动都会导致输出结果有较大的差异,它描述的是模型输出的预测值相比于真实值的离散程度,方差越大,越离散,所以为什么Bagging适合以不剪枝决策树、神经网络这些容易过拟合的模型为基学习器;
偏差大(方差低)的模型则相反,往往因为对训练数据拟合得不够,模型比较简单,输入数据发生变化并不会导致输出结果有多大改变,它描述的是预测值和和真实值直接的差距,偏差越大,越偏离真实值。
朴素贝叶斯中假设各特征相互独立,已经是很简化的模型了,所以其误差主要是在于偏差,没有方差可降。而 Bagging 主要关注降低方差,所以难以提升朴素贝叶斯分类器的性能。
ps:同样道理,这也是为什么8.5中,以决策树桩为基学习器的Bagging时,效果很差的原因;决策树桩同样是高偏差低方差的模型。
随机森林的起始性能往往相对较差, 特别是在集成中只包含一个基学习器时,这很容易理解,因为通过引入属性扰动,随机森林中个体学习器的性能往往有所降低。然而,随着个体学习器数目的增加,随机森林通常会收敛到更低的泛化误差。值得一提的是,随机森林的训练效率常优于Bagging,因为在个体决策树的构建过程中, Bagging 使用的是确定型决策树,在选择划分属性时要对结点的所有属性进行考察,而随机森林使用的随机型决策树则只需考察一个属性子集。
决策树的生成过程中,最耗时的就是搜寻最优切分属性;随机森林在决策树训练过程中引入了随机属性选择,大大减少了此过程的计算量;因而随机森林比普通决策树Bagging训练速度要快。

MultiBoosting由于集合了Bagging,Wagging,AdaBoost,可以有效的降低误差和方差,特别是误差,但是训练成本和预测成本都会显著增加。
Iterative Bagging相比Bagging会降低误差,但是方差上升。由于Bagging本身就是一种降低方差的算法,所以Iterative Bagging相当于Bagging与单分类器的折中。

暂无待补

暂无待补
