文章目录
〇、前言
这两周开始跟着【MOOC-浙江大学-陈越、何钦铭-数据结构】进行数据结构与算法的学习,特此记录复习一下,虽然记不住,但是一直记一直记一直记,成为复读机就好了。

一、基本概念
首先要确定的是什么是 数据结构和算法?
看到的一个解释,感觉很有意思,分享出来给大家看看。

原地址,想象一下有一条非常非常长的纸条,只能写一行字。
现在要把一些描述现实世界的东西写在这张纸条上,然后给别人。希望别人能通过纸条重构所描述的世界,或者在里面查找、推演出所需要的信息。
- 这张“纸条”就是信息的载体,包括硬盘、软盘、内存、甚至磁带,塑胶唱片,钢丝留声机,说白了都是一张转着圈或者拐着弯的纸条。
- “给别人”的过程就是读写硬盘过程、网络传输过程、无线电发报机滴滴哒哒收发信息的过程等等。
- 数据结构 所解决的问题就是,你怎么用一行字把这些复杂的东西描述出来,别人怎么读懂这些啰里吧嗦的东西(注:人看着啰嗦没事,机器看着不罗嗦就行)
- 编程,就是怎么解决3,怎么解决3之后解决重构出来的世界的一些具体问题…
结语:只要把我们的世界观从三维转到一维,就能学懂数据结构了…
哇,一下子就知道它是干啥的了,虽然没啥实际用途,不知道你们是怎么样,我总是想知道学的东西有啥用!
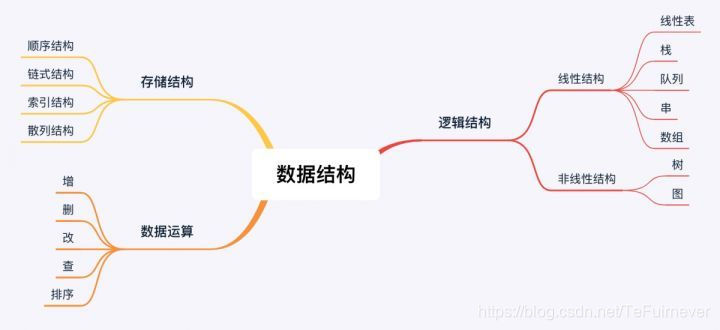
二、数据结构
- 解决问题方法的效率,跟数据的组织方式有关(堆栈还是队列)
- 解决问题方法的效率,跟空间的利用效率有关(循环还是递归)
- 解决问题方法的效率,跟算法的巧妙程度有关(硬算还是取巧)
所以不同的数据结构会有不同的优势和劣势,比如之前总结过的STL容器,【C++100问】深度总结STL基本容器的使用,vector 和 string 等等等等,不同的算法也是如此。
时间库的使用在计时方面是非常常用的,用于得到你的函数或者测试的部分的运行时间,当然你可能会说,IDE也会给出一个时间:
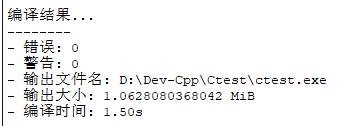
毫无疑问,这个时间是整个文件的编译时间。
不要忘记去调用 time.h,再就是除以 CLK_TCK !!!

很简单,直接套用就行了。
三、算法
1、定义
算法(Algorithm)
- 一个有限指令集
- 接受一些输入(有些情况下不需要输入)
- 产生输出
- 一定在有限步骤之后终止
- 每一条指令必须
- 有充分明确的目标,不可以有歧义
- 计算机能处理的范围之内
- 描述应不依赖于任何一种计算机语言以及具体的实现手段
2、如何衡量一个好的算法?
- 空间复杂度S(n) —— 根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限,造成程序非正常中断。
- 时间复杂度T(n) —— 根据算法写成的程序在执行时耗费时间的长度。这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。
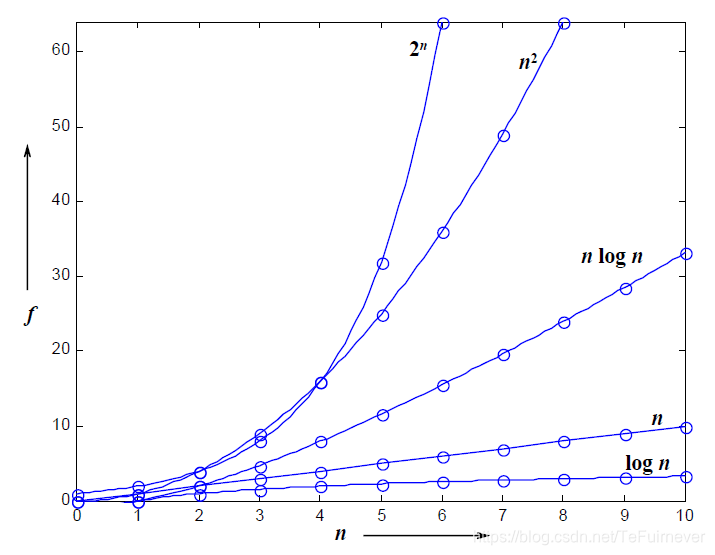
3、输入的规模和数量级有什么关系?
四、最大子列和问题
整个第一次课都在讨论的问题,最大子列和,也就是对子序列求和,然后求最大值。
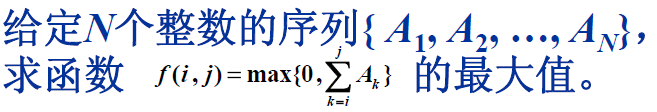
四个算法:
1、硬算

2、优化硬算

3、分而治之

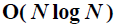
4、在线处理

五、课后题

1、01-复杂度1 最大子列和问题 (20分)

输入样例:
6
-2 11 -4 13 -5 -2
输出样例:
20
代码:
#include <stdio.h>
#define MAX 100001
int MaxSubseqSum4(int A[], int N);
int main()
{
int K=0;
scanf("%d", &K);
int i,A[MAX];
for(i=0;i<K;i++){
scanf("%d", &A[i]);
}
printf("%d", MaxSubseqSum4(A, K));
return 0;
}
int MaxSubseqSum4(int A[], int N){
int ThisSum, MaxSum;
int i;
ThisSum=MaxSum=0;
for(i=0;i<N;i++){
ThisSum+=A[i];
if(ThisSum>MaxSum)
MaxSum=ThisSum;
else if(ThisSum<0)
ThisSum=0;
}
return MaxSum;
}
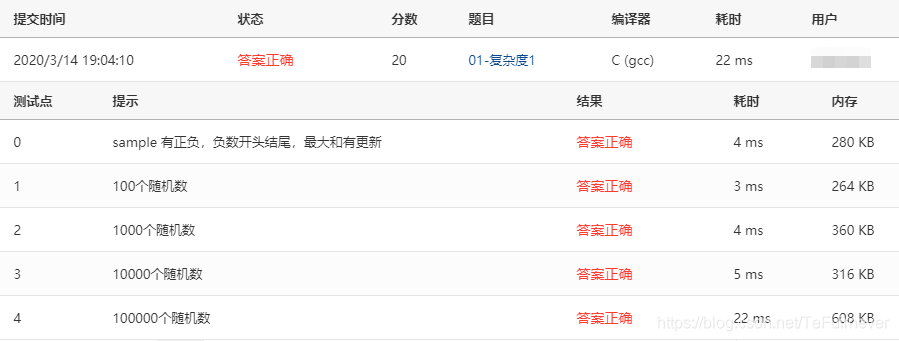
2、01-复杂度2 Maximum Subsequence Sum (25分)

Sample Input:
10
-10 1 2 3 4 -5 -23 3 7 -21
Sample Output:
10 1 4
代码:
#include <stdio.h>
#define MAX 100001
int MaxSubseqSum4(int A[], int N);
int main()
{
int K=0;
scanf("%d", &K);
int i,A[MAX];
for(i=0;i<K;i++){
scanf("%d", &A[i]);
}
MaxSubseqSum4(A, K);
return 0;
}
int MaxSubseqSum4(int A[], int N){
int ThisSum, MaxSum;
int i,j;
int start=A[0], end;
ThisSum=MaxSum=0;
int s=A[0];
for(i=0;i<N;i++){
ThisSum+=A[i];
if(ThisSum>MaxSum){
MaxSum=ThisSum;
end=A[i];
start=s;
}
else if(ThisSum<0){
ThisSum=0;
if (A[i]!=0)
s=A[i+1];
}
}
if(MaxSum==0){
start=A[0];
end=A[N-1];
for(j=0;j<N;j++){
if(A[j]==0){
start=0;
end=0;
}
}
}
printf("%d %d %d", MaxSum, start, end);
return;
}
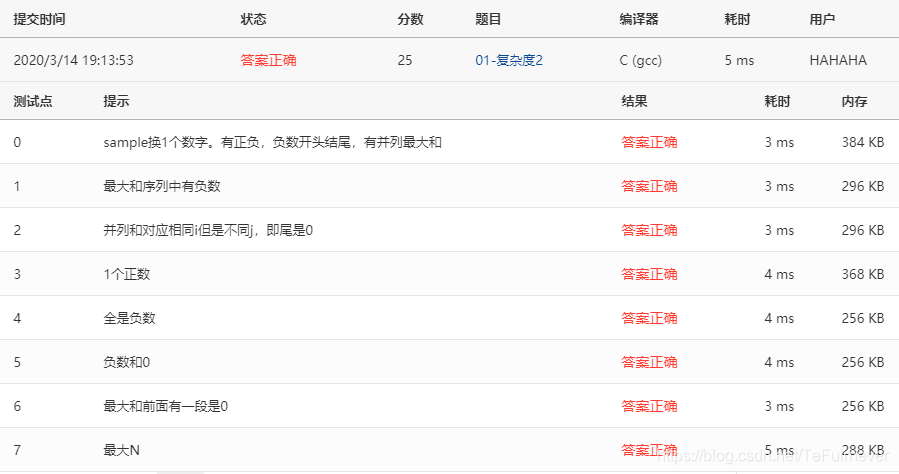
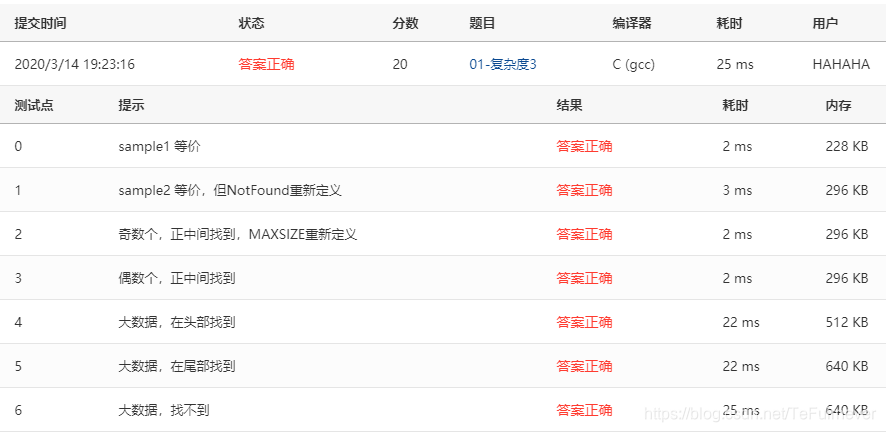
3、01-复杂度3 二分查找 (20分)
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
#define NotFound 0
typedef int ElementType;
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
List ReadInput(); /* 裁判实现,细节不表。元素从下标1开始存储 */
Position BinarySearch( List L, ElementType X );
int main()
{
List L;
ElementType X;
Position P;
L = ReadInput();
scanf("%d", &X);
P = BinarySearch( L, X );
printf("%d
", P);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例1:
5
12 31 55 89 101
31
输出样例1:
2
输入样例2:
3
26 78 233
31
输出样例2:
0
Position BinarySearch( List L, ElementType X )
{
Position p=NotFound;
int left=1,right=L->Last, mid;
while(left<=right)
{
mid=(left+right)/2;
if(X==L->Data[mid]) return mid;
else if(X<L->Data[mid]) right=mid-1;
else if(X>L->Data[mid]) left=mid+1;
}
return p;
}
总结
简单总结下这周的学习内容,初步接触了数据结构与算法,感觉自己太菜,,,还是得手撕代码!!!
如果想要更多的资源,欢迎关注 @我是管小亮,文字强迫症MAX~
回复【数据结构】即可获取我为你准备的大礼
想看更多文(段)章(子),欢迎关注微信公众号「程序员管小亮」~
