再也不怕女朋友问我二分查找了！【手绘漫画】图解二分查找（修订版）（LeetCode 704题）

文章目录

• 图解算法与数据结构
• 1、前言
• 2、代码
• 3、实例（LeetCode 704题）

图解算法与数据结构

1、前言

上次讲到的更的二分查找模板在很多地方让我使用起来不是特别的舒服，感谢B站上的y大佬，让我找到了一个新的模板！！！

下面一起来看看吧！！！

本次的模板应对重复元素也可以~

2、代码

模板一：

// C
int lower_bound(int* nums, int numsSize, int target){
	int left = 0;
	int right = numsSize-1;
	while(left < right){	// 搜索区间[first, last)不为空
		// 防溢出
		int mid = left + right >> 1;
		if(nums[mid] >= target) right = mid;
		else left = mid + 1;
	}
	return left;			// right也行，因为[left, right)为空的时候它们重合
}

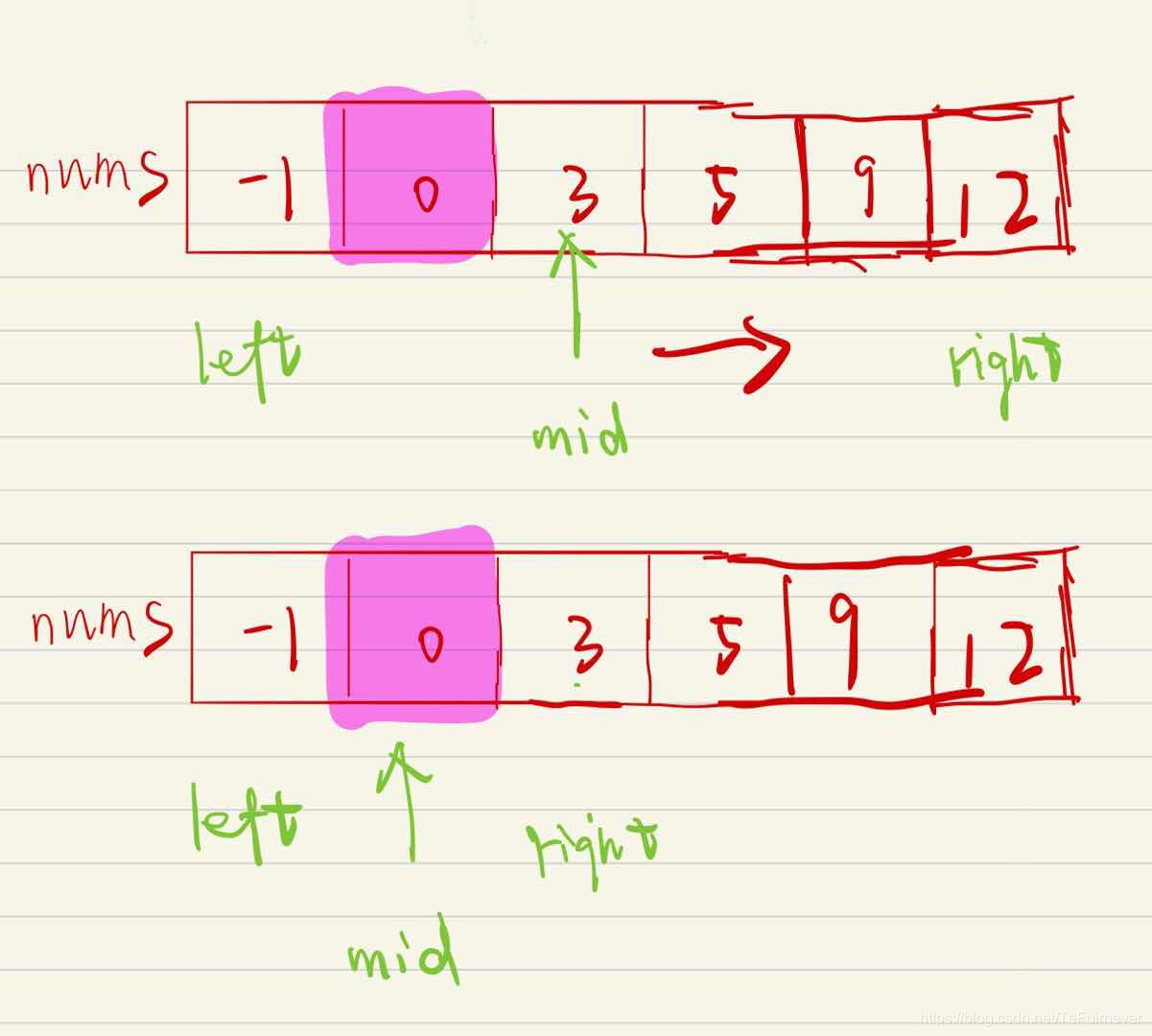
首先一定要明确，数组是升序的！！！

如果中点大于等于 target，表示目标在左侧，数组范围应该从 [left, right] 变成 [left, mid]，否则，就从 [left, right] 变成 [mid+1, right]。

为什么 right 不加一？

因为是大于等于，带着等于，也就是 mid 有可能是我们的解！！！

---

模板二：

// C
int lower_bound(int* nums, int numsSize, int target){
	int left = 0;
	int right = numsSize-1;
	while(left < right){	// 搜索区间[first, last)不为空
		// 防溢出
		int mid = left + right + 1 >> 1; // 防止死循环，mid加1
		if(nums[mid] <= target) left = mid;
		else right = mid + 1;
	}
	return left;			// right也行，因为[left, right)为空的时候它们重合
}

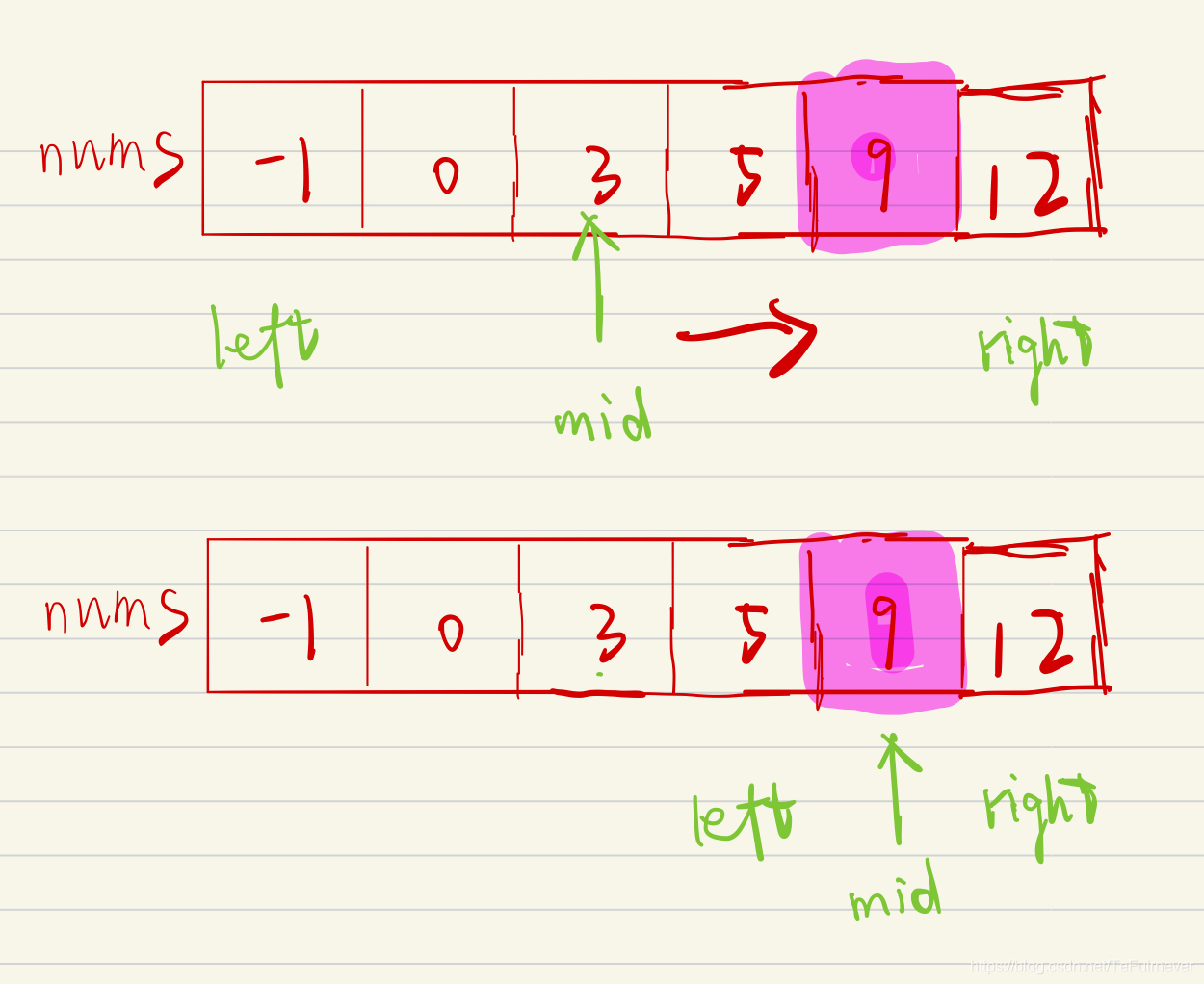
首先一定要明确，数组是升序的！！！

如果中点小于等于 target，表示目标在右侧，数组范围应该从 [left, right] 变成 [mid, right]，否则，就从 [left, right] 变成 [left, mid+1]。

为什么 left 不加一？

因为是小于等于，带着等于，也就是 mid 有可能是我们的解！！！

• 模板一：区间 [left, right] 划分成 [left, mid] 和 [mid + 1, right] 时，其更新操作是 right = mid 或者 left = mid + 1;，计算 mid 时不需要加 1。
• 模板二：区间 [left, right] 划分成 [left, mid - 1] 和 [mid, right] 时，其更新操作是 r = mid - 1 或者 l = mid;，此时为了防止死循环，计算 mid 时需要加 1。

3、实例（LeetCode 704题）

首先看一下题目，

代码：

int search(int* nums, int numsSize, int target){
    int left=0;
    int right=numsSize-1;
    while(left<right){
        int mid=left+right >> 1;
        if(nums[mid]>=target){
            right=mid;
        }
        else{
            left=mid+1;
        }
    }
    if(nums[left]==target) return left;
    return -1;
}

作为最经典的二分查找题，这个题依旧复合我们的模板，没错就是 模板一！！！

唯一不同的是，要注意判断结果，不能只写个 left ，因为是存在 -1 的情况的，加个 if(nums[left]==target) return left; 就好了。

这里自然又更容易的方法，但是 练习模板，万法接通，每日一遍，养成习惯！！！

附上最经典的二分查找解法：

// C
int search(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize - 1;

    while (left <= right) {
    	// 最好这么写，不然会内存溢出
    	// 同时还能减少运行时间！！！
        int mid = (left + right) >> 1;
        // 等于的情况最简单，首先判断，没准一下就中了！
        if (nums[mid] == target) {
            return mid;
        }
        else if (nums[mid] < target) {
            // 左边界更新为 mid + 1
            left = mid + 1;
        }
        else {
            // 右边界更新为 mid - 1
            right = mid - 1;
        }
    }
    return -1;
}

如果有幸帮到你，请帮我点个【赞】，给个【关注】！如果能顺带【评论】给个鼓励，我将不胜感激。

如果想要更多的资源，欢迎关注 @我是管小亮，文字强迫症MAX~