一个菜鸟对于堆排序的理解

N个元素称为堆，若它的元素序列k[1]，k[2]，k[3]…K[n]满足

   k[i]<=k[2i]  ，k[i]<=k[2i+1]     1<=i<=n/2

则称之为最小堆（min_heaps）， 如果满足

  k[i]>=k[2i]  ，k[i]>=k[2i+1]     1<=i<=n/2

则称之为最大堆（min_heaps）。

用图来理解的话

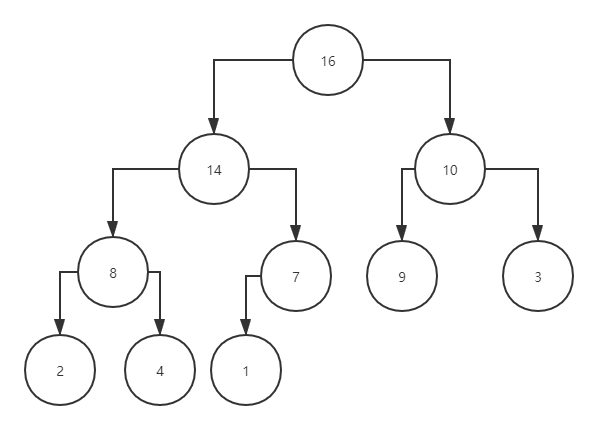
图中对顶端的元素最大为大根堆,最小为小根堆(该图为大根堆)

建立一个堆只需要将元素一个一个插入即可,自上而下建堆的时间复杂度为O(n*log2n)插入元素时需保证堆顶元素始终最大(最小),而自下而上的建堆方
式是从第一个非叶子节点开始建堆,注意将最大(最小)元素交换到堆顶.
下面是一个自上而下建堆的动态演示网站
https://bajdcc.github.io/html/heap.html

我们不难看出堆是无须的.
堆得排序
假设堆有n个元素，由于堆的第一个元素一定是最大的元素，因此可以让第一个元素和第n个元素互换，然后对第一个元素执行下操作。接着，对n-1个元素执行相同的操作，让第一个元素与第n-1个元素互换，然后对第一个元素执行下移操作，依次类推，最后的堆就是从小到大排序好的堆。

void heap_sort(int *H,int m)
{
	for(int i=m;i>0;i--)
	{
		swap(H[i],H[1]);
		sift_down(H,i-1,1); 
	}
}

堆的插入
插入到堆最后1个元素后面，然后对该元素执行上移操作

堆的修改
如果修改堆中某个元素，使得它的值大于父节点的，这就破坏了最大堆的性质，因此需要对堆实现上移操作。
如果修改堆中某个元素，使得它的值小于孩子节点，这就破坏了最大堆的性质，因此需要对堆实现下移操作。

堆的删除操作
如果我们要删除下标为 i 的元素，那么我们可以用堆中最后1个元素替代i，然后对这个替代后的元素执行上移或者下移操作
完整代码如下

 //构建大根堆：将array看成完全二叉树的顺序存储结构
      private int[] buildMaxHeap(int[] array){
          //从最后一个节点array.length-1的父节点（array.length-1-1）/2开始，直到根节点0，反复调整堆
          for(int i=(array.length-2)/2;i>=0;i--){ 
              adjustDownToUp(array, i,array.length);
          }
          return array;
      }
      
     //将元素array[k]自下往上逐步调整树形结构
     private void adjustDownToUp(int[] array,int k,int length){
         int temp = array[k];   
         for(int i=2*k+1; i<length-1; i=2*i+1){    //i为初始化为节点k的左孩子，沿节点较大的子节点向下调整
             if(i<length && array[i]<array[i+1]){  //取节点较大的子节点的下标
                 i++;   //如果节点的右孩子>左孩子，则取右孩子节点的下标
             }
             if(temp>=array[i]){  //根节点 >=左右子女中关键字较大者，调整结束
                 break;
             }else{   //根节点 <左右子女中关键字较大者
                 array[k] = array[i];  //将左右子结点中较大值array[i]调整到双亲节点上
                 k = i; //【关键】修改k值，以便继续向下调整
             }
         }
         array[k] = temp;  //被调整的结点的值放人最终位置
     }    
 //删除堆顶元素操作
     public int[] deleteMax(int[] array){
         //将堆的最后一个元素与堆顶元素交换，堆底元素值设为-99999
         array[0] = array[array.length-1];
         array[array.length-1] = -99999;
         //对此时的根节点进行向下调整
         adjustDownToUp(array, 0, array.length);
         return array;
     }
 //插入操作:向大根堆array中插入数据data
      public int[] insertData(int[] array, int data){
          array[array.length-1] = data; //将新节点放在堆的末端
          int k = array.length-1;  //需要调整的节点
          int parent = (k-1)/2;    //双亲节点
          while(parent >=0 && data>array[parent]){
              array[k] = array[parent];  //双亲节点下调
              k = parent;
              if(parent != 0){
                 parent = (parent-1)/2;  //继续向上比较
             }else{  //根节点已调整完毕，跳出循环
                 break;
             }
         }
        array[k] = data;  //将插入的结点放到正确的位置
         return array;
     }

本文并不是完全一篇原创文,希望能对你有所帮助.