cf div2 234 D

D. Dima and Bacteria

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Dima took up the biology of bacteria, as a result of his experiments, he invented k types of bacteria. Overall, there are n bacteria at his laboratory right now, and the number of bacteria of type i equals c_i. For convenience, we will assume that all the bacteria are numbered from 1 to n. The bacteria of type c_i are numbered from 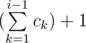to .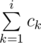

With the help of special equipment Dima can move energy from some bacteria into some other one. Of course, the use of such equipment is not free. Dima knows m ways to move energy from some bacteria to another one. The way with number i can be described with integers u_i, v_i and x_i mean that this way allows moving energy from bacteria with number u_i to bacteria with number v_i or vice versa for x_i dollars.

Dima's Chef (Inna) calls the type-distribution correct if there is a way (may be non-direct) to move energy from any bacteria of the particular type to any other bacteria of the same type (between any two bacteria of the same type) for zero cost.

As for correct type-distribution the cost of moving the energy depends only on the types of bacteria help Inna to determine is the type-distribution correct? If it is, print the matrix d with size k × k. Cell d[i][j] of this matrix must be equal to the minimal possible cost of energy-moving from bacteria with type i to bacteria with type j.

Input

The first line contains three integers n, m, k (1 ≤ n ≤ 10⁵; 0 ≤ m ≤ 10⁵; 1 ≤ k ≤ 500). The next line contains k integers c₁, c₂, ..., c_k (1 ≤ c_i ≤ n). Each of the next m lines contains three integers u_i, v_i, x_i (1 ≤ u_i, v_i ≤ 10⁵; 0 ≤ x_i ≤ 10⁴). It is guaranteed that .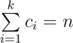

Output

If Dima's type-distribution is correct, print string «Yes», and then k lines: in the i-th line print integers d[i][1], d[i][2], ..., d[i][k] (d[i][i] = 0). If there is no way to move energy from bacteria i to bacteria j appropriate d[i][j] must equal to -1. If the type-distribution isn't correct print «No».

Sample test(s)

Input

4 4 2
1 3
2 3 0
3 4 0
2 4 1
2 1 2

Output

Yes
0 2
2 0

Input

3 1 2
2 1
1 2 0

Output

Yes
0 -1
-1 0

Input

3 2 2
2 1
1 2 0
2 3 1

Output

Yes
0 1
1 0

Input

3 0 2
1 2

Output

No

好吧，cf第四道居然这么水，虽然死长死长的，每个类型中取一个点深搜只走权为0的路，然后判断能不能覆盖同类型的所有点即可判断，然后更新dis[i][j] ( 1<=i<= k, 1<=j<=k)的值，走一次floyd即可

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>

using namespace std;

#define maxn 100005

int n,m,k;
int c[505],first[maxn],next[2 * maxn],v[2 * maxn],x[2 * maxn],dis[505][505],u1[2 * maxn];
bool flag = 1;
bool vis[maxn];

void addedge(int a,int b,int id) {
        int e = first[a];
        next[id] = e;
        first[a] = id;
}

void dfs(int u,int type) {
        vis[u] = 1;
        //printf("u = %d type = %d
",u,type);
        for(int e = first[u]; e != -1; e = next[e]) {
                if(!vis[ v[e] ] && x[e] == 0) {
                        dfs(v[e],type);
                }
        }
}
void solve() {
        for(int i = 1; i <= k; i++) {
                memset(vis,0,sizeof(vis));
                dfs(c[i],i);

                for(int j = c[i - 1] + 1; j <= c[i]; j++) {
                        if(!vis[j]) {
                            flag = 0;
                            //printf(" i = %d
",i);
                            return;
                        }
                }

        }
}

void floyd() {
        for(int p = 1; p <= k; p++) {
                for(int i = 1; i <= k; i++) {
                        for(int j = 1; j <= k; j++) {
                                if(dis[i][p] != -1 && dis[p][j] != -1) {
                                         dis[i][j] = dis[i][j] == -1 ? dis[i][p] + dis[p][j] :
                                                    min(dis[i][j],dis[i][p] + dis[p][j]);
                                }
                        }
                }
        }
}
void output() {
        if(flag) {
                printf("Yes
");

                for(int i = 0; i < 2 * m; i += 2 ) {
                        int id1,id2;
                        id1 = lower_bound(c + 1,c + k + 1,u1[i]) - c;
                        id2 = lower_bound(c + 1,c + k + 1,v[i]) - c;
                        if(id1 == id2) continue;
                        dis[id1][id2] = dis[id2][id1] = dis[id1][id2] == -1 ?
                                        x[i] : min(dis[id1][id2],x[i]);
                }

                floyd();

                for(int i = 1; i <= k; i++) {
                        for(int j = 1; j <= k; j++) {
                                printf("%d",dis[i][j]);
                                if(j != k) printf(" ");
                        }
                        printf("
");
                }
        } else {
                printf("No
");
        }
}


int main() {

        freopen("sw.in","r",stdin);

        scanf("%d%d%d",&n,&m,&k);

        for(int i = 1; i <= k; i++) {
                scanf("%d",&c[i]);
        }

        for(int i = 1; i <= k; i++) {
                c[i] += c[i - 1];
        }

        for(int i = 1; i <= k; i++) {
                for(int j = 1; j <= k; j++) {
                        if(i == j) dis[i][j] = 0;
                        else dis[i][j] = -1;
                }
        }


        for(int i = 1; i <= n; i++) first[i] = -1;

        for(int i = 0; i < 2 * m; i = i + 2) {
                int a,b,w;
                scanf("%d%d%d",&u1[i],&v[i],&x[i]);
                v[i + 1] = u1[i];
                u1[i + 1] = v[i];
                x[i + 1] = x[i];
                addedge(u1[i],v[i],i);
                addedge(v[i],u1[i],i + 1);
        }

        solve();

        output();

        return 0;


}