一、对数

二、代码
1 def binary_search(lists, item):
2 # low和high用于跟踪要在其中查找的列表的部分
3 low = 0
4 high = len(lists)-1
5
6 while low <= high: # 只要范围没有缩小到只包含一个元素
7 mid = (low + high)/2 #就检查中间的元素
8
9 guess = lists[mid]
10 if guess == item: #找到元素
11 return mid
12 if guess > item: # 猜的数字大了
13 high = mid-1
14 else: # 差的数字小了
15 low = mid+1
16 # 没有指定的元素
17 return None
18
19 my_list = [1, 3, 5, 7, 9]
20 print(len(my_list))
21 print (binary_search(my_list, 3))
22 print (binary_search(my_list, -1))
三、运行时间
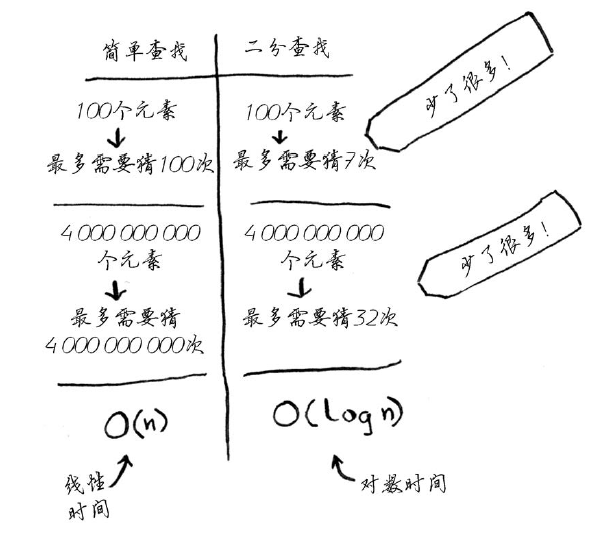
如果列表包含100个元素,最多要猜7次;
如果列表包含40亿个数字,最多需猜32次。二分查找的运行时间为对数时间(或log时间)
四、大O表示法
大O表示法是一种特殊的表示法,指出了算法的速度有多快。
大O表示法指出了算法有多快。例如,假设列表包含n个元素。简单查找需要检查每个元素,因此需要执行n次操作。使用大O表示法,这个运行时间为O(n)。
单位秒呢?没有——大O表示法指的并非以秒为单位的速度。
大O表示法让你能够比较操作数,它指出了算法运行时间的增速。
下面按从快到慢的顺序列出了你经常会遇到的5种大O运行时间。
1、O(log n),也叫对数时间,这样的算法包括二分查找。
2、O(n),也叫线性时间,这样的算法包括简单查找。
3、O(n * log n),这样的算法包括第4章将介绍的快速排序——一种速度较快的排序算法。
4、O(n2),这样的算法包括第2章将介绍的选择排序——一种速度较慢的排序算法。
5、O(n!),这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法。
说明
1、仅当列表是有序的时候,二分查找才管用。
2、谈论算法的速度时,我们说的是随着输入的增加,其运行时间将以什么样的速度增加。
3、算法的运行时间用大O表示法表示。
4、O(log n)比O(n)快,当需要搜索的元素越多时,前者比后者快得越多。
5、算法运行时间并不以秒为单位。
参考书籍:算法图解