Java中的二进制及基本的位运算

Java中的二进制及基本的位运算

　　二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”，由18世纪德国数理哲学大师莱布尼兹发现。当前的计算机系统使用的基本上是二进制系统，数据在计算机中主要是以补码的形式存储的。计算机中的二进制则是一个非常微小的开关，用“开”来表示1，“关”来表示0。

　　那么Java中的二进制又是怎么样的呢？让我们一起来揭开它神秘的面纱吧。

一、Java内置的进制转换

有关十进制转为二进制，和二进制转为十进制这种基本的运算方法这里就不展开讲了。

在Java中内置了几个方法来帮助我们进行各种进制的转换。如下图所示（以Integer整形为例，其他类型雷同）：

1，十进制转化为其他进制：

二进制：Integer.toHexString(int i);
八进制：Integer.toOctalString(int i);
十六进制：Integer.toBinaryString(int i);

2,其他进制转化为十进制：

二进制：Integer.valueOf("0101",2).toString;
八进制：Integer.valueOf("376",8).toString;
十六进制：Integer.valueOf("FFFF",16).toString;

3,使用Integer类中的parseInt()方法和valueOf()方法都可以将其他进制转化为10进制。

不同的是parseInt()方法的返回值是int类型，而valueOf()返回值是Integer对象。

二、基本的位运算

二进制可以和十进制一样加减乘除，但是它还有更简便的运算方式就是——位运算。比如在计算机中int类型的大小是32bit，可以用32位的二进制数来表示，所以我们可以用位运算来对int类型的数值进行计算，当然你也可以用平常的方法来计算一些数据，这里我主要为大家介绍位运算的方法。我们会发现位运算有着普通运算方法不可比拟的力量。更多位运算应用请转移到我下篇博文《神奇的位运算》

首先，看一下位运算的基本操作符：

优点：

• 特定情况下，计算方便，速度快，被支持面广
• 如果用算数方法，速度慢，逻辑复杂
• 位运算不限于一种语言，它是计算机的基本运算方法

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

（一）按位与&

两位全为1，结果才为1

0&0=0；0&1=0；1&0=0；1&1=1

例如：51&5 即0011 0011 & 0000 0101 =0000 0001 因此51&5=1.

特殊用法

（1）清零。如果想将一个单元清零，即使其全部二进制位为0，只要与一个各位都是零的数值相与，结果为零。

（2）取一个数中指定位。

例如：设X=10101110，取X的低四位，用X&0000 1111=0000 1110即可得到。

方法：找一个数，对应x要取的位，该数的对应位为1，其余位为零，此数与x进行“与运算”可以得到x中的指定位。

（二）按位或 |

只要有一个为1，结果就为1。

0|0=0； 0|1=1；1|0=1；1|1=1；

例如：51|5 即0011 0011 | 0000 0101 =0011 0111 因此51|5=55

 特殊用法

常用来对一个数据的某些位置1。

方法：找到一个数，对应x要置1的位，该数的对应位为1，其余位为零。此数与x相或可使x中的某些位置1。

（三）异或 ^

两个相应位为“异”（值不同），则该位结果为1，否则为0

0^0=0; 0^1=1; 1^0=1; 1^1=0;

例如：51^5 即0011 0011 ^ 0000 0101 =0011 0110 因此51^5=54

特殊用法

（1）  与1相异或，使特定位翻转

方法：找一个数，对应X要翻转的位，该数的对应为1，其余位为零，此数与X对应位异或即可。

例如：X=1010 1110，使X低四位翻转，用X^0000 1111=1010 0001即可得到。

（2）  与0相异或，保留原值

例如：X^0000 0000 =1010 1110

（3）两个变量交换值

1.借助第三个变量来实现

C=A;A=B;B=C;

2.利用加减法实现两个变量的交换

 A=A+B;B=A-B;A=A-B;

3.用位异或运算来实现，也是效率最高的

原理：一个数异或本身等于0 ；异或运算符合交换律

A=A^B;B=A^B;A=A^B

（四）取反与运算~

对一个二进制数按位取反，即将0变为1，1变0

~1=0 ；~0=1

（五）左移<<

将一个运算对象的各二进制位全部左移若干位（左边的二进制位丢弃，右边补0）

例如： 2<<1 =4    10<<1=100

若左移时舍弃的高位不包含1，则每左移一位，相当于该数乘以2。

例如：

       11(1011)<<2= 0010 1100=22

       11(00000000 00000000 00000000 1011)整形32bit

（六）右移>>

将一个数的各二进制位全部右移若干位，正数左补0，负数左补1，右边丢弃。若右移时舍高位不是1（即不是负数），操作数每右移一位，相当于该数除以2。

左补0还是补1得看被移数是正还是负。

例如：4>>2=4/2/2=1

        -14（即1111 0010）>>2 =1111 1100=-4

（七）无符号右移运算>>>

各个位向右移指定的位数，右移后左边空出的位用零来填充，移除右边的位被丢弃。

例如：-14>>>2

（即11111111 11111111 11111111 11110010）>>>2

=(00111111 11111111 11111111 11111100)=1073741820

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

上述提到的负数，他的二进制位表示和正数略有不同，所以在位运算的时候也与正数不同。

负数以其正数的补码形式表示！

以上述的-14为例，来简单阐述一下原码、反码和补码。

原 码

一个整数按照绝对值大小转化成的二进制数称为原码

例如：00000000 00000000 00000000 00001110 是14的原码。

反 码

将二进制数按位取反，所得到的新二进制数称为原二进制数的反码。

例如：将00000000 00000000 00000000 00001110 每一位取反，

得11111111 11111111 11111111 11110001

注意：这两者互为反码

补 码

反码加1称为补码

11111111 11111111 11111111 11110001 +1=

11111111 11111111 11111111 11110010

现在我们得到-14的二进制表示，现在将它左移

-14（11111111 11111111 11111111 11110010）<<2 =

11111111 11111111 11111111 11001000

=？

分析：这个二进制的首位为1，说明是补码形式，现在我们要将补码转换为原码（它的正值）

跟原码转换为补码相反，将补码转换为原码的步骤：

1. 补码减1得到反码：（11000111）前24位为1，此处省略
2. 反码取反得到原码（即该负数的正值）（00111000）
3. 计算正值，正值为56
4. 取正值的相反数，得到结果-56

结论：-14<<2 = -56

三、Java中进制运算

Java中二进制用的多吗？

平时开发中“进制转换”和“位操作”用的不多，Java处理的是高层。

在跨平台中用的较多，如：文件读写，数据通信。

来看一个场景：

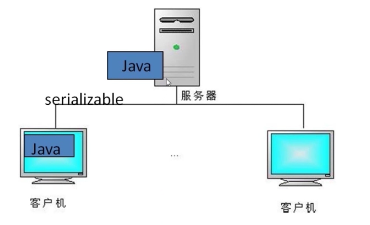
如果客户机和服务器都是用Java语言写的程序，那么当客户机发送对象数据，我们就可以把要发送的数据序列化serializable，服务器端得到序列化的数据之后就可以反序列化，读出里面的对象数据。

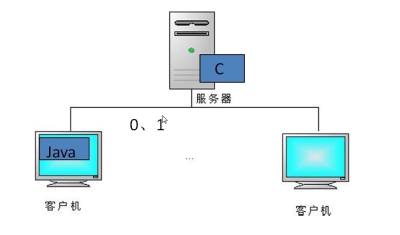
随着客户机访问量的增大，我们不考虑服务器的性能，其实一个可行的方案就是把服务器的Java语言改成C语言。

C语言作为底层语言，反映速度都比Java语言要快，而此时如果客户端传递的还是序列化的数据，那么服务器端的C语言将无法解析，怎么办呢？我们可以把数据转为二进制（0，1），这样的话服务器就可以解析这些语言。

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

Java中基本数据类型有以下四种：

1. Int数据类型：byte（8bit，-128~127）、short（16bit）、int（32bit）、long（64bit）
2. float数据类型：单精度（float，32bit ） 、双精度（double,64bit）
3. boolean类型变量的取值有true、false（都是1bit）
4. char数据类型：unicode字符，16bit

对应的类类型：

Integer、Float、Boolean、Character、Double、Short、Byte、Long

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

（一）数据类型转为字节

例如：int型8143（00000000 00000000 00011111 11001111）

=>byte[] b=[-49,31,0,0]

第一个（低端）字节：8143>>0*8 & 0xff=(11001111)=207（或有符号-49）

第二个（低端）字节：8143>>1*8 &0xff=(00011111)=31

第三个（低端）字节：8143>>2*8 &0xff=00000000=0

第四个（低端）字节：8143>>3*8 &0xff=00000000=0

我们注意到上面的（低端）是从右往左开始的，那什么是低端呢？我们从大小端的角度来说明。

小端法（Little-Endian）

低位字节排放在内存的低地址端即该值的起始地址，高位字节排位在内存的高地址端

大端法（Big-Endian）

高位字节排放在内存的低地址端即该值的起始地址，低位字节排位在内存的高地址端

为什么会有大小端模式之分呢？

这是因为在计算机系统中，我们是以字节为单位的，每个地址单元都对应着一个字节，一个字节为8bit。但是在C语言中除了8bit的char之外，还有16bit的short型，32bit的long型（要看具体的编译器），另外，对于位数大于8位的处理器，例如16位或者32位的处理器，由于寄存器宽度大于一个字节，那么必然存在着一个如果将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。例如一个16bit的short型x，在内存中的地址为0x0010，x的值为0x1122，那么0x11为高字节，0x22为低字节。对于大端模式，就将0x11放在低地址中，即0x0010中，0x22放在高地址中，即0x0011中。小端模式，刚好相反。我们常用的X86结构是小端模式，而KEIL C51则为大端模式。很多的ARM，DSP都为小端模式。有些ARM处理器还可以由硬件来选择是大端模式还是小端模式。

例如：32bit的数0x12 34 56 78（十二进制）

在Big-Endian模式CPU的存放方式（假设从地址0x4000开始存放）为

内存地址	0x4000	0x4001	0x4002	0x4003
存放内容	0x78	0x56	0x34	0x12

在Little-Endian模式CPU的存放方式（假设从地址0x4000开始存放）为

内存地址	0x4000	0x4001	0x4002	0x4003
存放内容	0x12	0x34	0x56	0x78

 （二）字符串转化为字节

1.字符串->字节数组

String s;
byte[] bs=s.getBytes();

2.字节数组->字符串

Byte[] bs=new byte[int];
String s =new String(bs);或
String s=new String(bs,encode);//encode指编码方式，如utf-8

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

两种类型转化为字节的方法都介绍了，下面写个小例子检验一下：

public class BtyeTest {
    /*
     * int整型转为byte字节
     */
    public static byte[] intTOBtyes(int in){
        byte[] arr=new byte[4];
        for(int i=0;i<4;i++){
            arr[i]=(byte)((in>>8*i) & 0xff);
        }
        return arr;
    }
    /*
     * byte字节转为int整型
     */
    public static int bytesToInt(byte[] arr){
        int sum=0;
        for(int i=0;i<arr.length;i++){
            sum+=(int)(arr[i]&0xff)<<8*i;
        }
        return sum;
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        byte[] arr=intTOBtyes(8143);
        for(byte b:arr){
            System.out.print(b+" ");
        }
        System.out.println();
        System.out.println(bytesToInt(arr));
        
        //字符串与字节数组
        String str="云开的立夏de博客园";
        byte[] barr=str.getBytes();
        
        String str2=new String(barr);
        System.out.println("字符串转为字节数组：");
        for(byte b:barr){
            System.out.print(b+" ");

        }
        System.out.println();

        System.out.println("字节数组换位字符串："+str2);
        
         
    }

}

运行结果：

---

结束语：最近偷懒了，没有好好学习，好几天没写文了，哎，还请大家多多监督！