2018-10-06 19:44:18
问题描述:
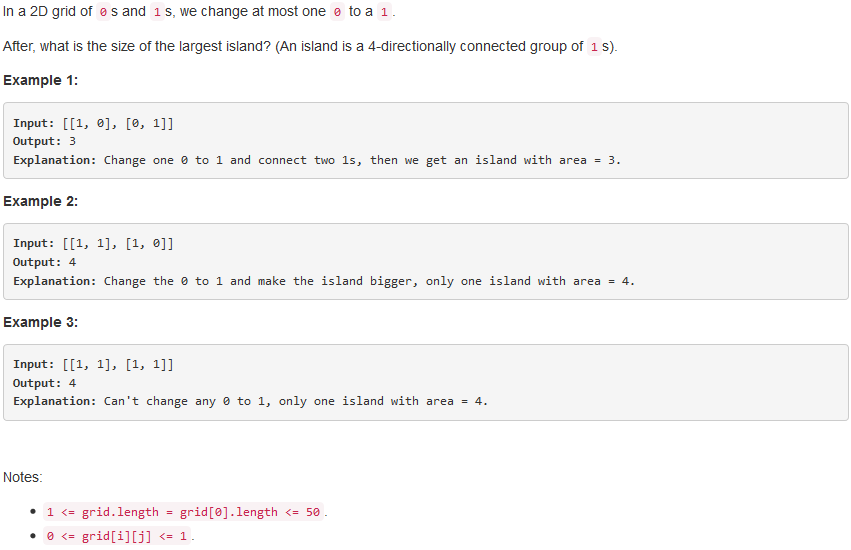
问题求解:
经典的求连通块问题的扩展,问题规模不大,可以暴力求解。
解法一、Brute Force O(n^4)
int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int largestIsland(int[][] grid) {
int res = Integer.MIN_VALUE;
int n = grid.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) res = Math.max(res, helper(grid, i, j, new int[n][n]));
else {
grid[i][j] = 1;
res = Math.max(res, helper(grid, i, j, new int[n][n]));
grid[i][j] = 0;
}
}
}
return res;
}
private int helper(int[][] grid, int x, int y, int[][] used) {
int n = grid.length;
int res = 1;
used[x][y] = 1;
for (int[] dir : dirs) {
int px = x + dir[0];
int py = y + dir[1];
if (px < 0 || px >= n || py < 0 || py >= n || used[px][py] == 1 || grid[px][py] == 0) continue;
res += helper(grid, px, py, used);
}
return res;
}
解法二、
为每个连通块做上标记,并得到每个连通块的面积,之后再对0进行遍历,依次寻找其四个相邻的边的area,将他们加起来再从中取max。算法总的时间复杂度为O(n ^ 2)。
public int largestIsland(int[][] grid) {
int res = Integer.MIN_VALUE;
int n = grid.length;
Map<Integer, Integer> map = new HashMap<>();
int color = 0;
int area = 0;
map.put(color++, area);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) area = dfs(grid, i, j, ++color);
map.put(color, area);
res = Math.max(res, area);
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 0) {
int curArea = 1;
Set<Integer> set = new HashSet<>();
set.add(getColor(grid, i - 1, j));
set.add(getColor(grid, i + 1, j));
set.add(getColor(grid, i, j + 1));
set.add(getColor(grid, i, j - 1));
for (int c : set) {
curArea += map.get(c);
}
res = Math.max(res, curArea);
}
}
}
return res;
}
private int getColor(int[][] grid, int x, int y) {
if (x < 0 || x >= grid.length || y < 0 || y >= grid.length) return 0;
else return grid[x][y];
}
private int dfs(int[][] grid, int x, int y, int color) {
if (x < 0 || x >= grid.length || y < 0 || y >= grid.length || grid[x][y] != 1) return 0;
grid[x][y] = color;
return 1 + dfs(grid, x + 1, y, color) + dfs(grid, x - 1, y, color) +
dfs(grid, x, y - 1, color) + dfs(grid, x, y + 1, color);
}