2018-04-22 19:59:52
Sum系列的问题是Leetcode上的一个很经典的系列题,这里做一个简单的总结。
-
167. Two Sum II - Input array is sorted
问题描述:

问题求解:
对于已排序的问题,可以使用双指针在O(n)的时间复杂度内完成求解。
// 已排序数组,返回indices
public int[] twoSum(int[] numbers, int target) {
int i = 0;
int j = numbers.length - 1;
while (i < j) {
if (target > numbers[i] + numbers[j]) i++;
else if (target < numbers[i] + numbers[j]) j--;
else break;
}
return new int[]{i + 1, j + 1};
}
-
1. Two Sum
问题描述:

问题求解:
可以使用数据结构中的hash来很高效的解决,具体来说,我们可以建立一个hashmap,用来保存数值和其index,遍历数组,如果说hashmap中存在target - nums[i],由于题目中明确了只有唯一的解,因此就可以直接确定结果,将这两个数的index返回即可。
public int[] twoSum3(int[] numbers, int target) {
int[] result = new int[2];
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < numbers.length; i++) {
if (map.containsKey(target - numbers[i])) {
result[1] = i + 1;
result[0] = map.get(target - numbers[i]);
break;
}
map.put(numbers[i], i + 1);
}
return result;
}
-
653. Two Sum IV - Input is a BST
问题描述:
Given a Binary Search Tree and a target number, return true if there exist two elements in the BST such that their sum is equal to the given target.
问题求解:
方法一、很容易想到的是二叉搜索树的中序遍历是一个有序数列,如果我们采用中序遍历一次并保存下来,那么问题就变成了上述的已排序数组求two sum的问题。
代码时间复杂度为O(n)。
ArrayList<Integer> ls = new ArrayList<>();
public boolean findTarget(TreeNode root, int k) {
inOrder(root);
boolean res = false;
int i = 0;
int j = ls.size() - 1;
while (i < j) {
if (ls.get(i) + ls.get(j) > k) j--;
else if (ls.get(i) + ls.get(j) < k) i++;
else {
res = true;
break;
}
}
return res;
}
void inOrder(TreeNode root) {
if (root != null) {
inOrder(root.left);
ls.add(root.val);
inOrder(root.right);
}
}
方法二、递归遍历,每次递归到某个数就对target - nums[i]进行查找,值得注意的是,在查找过程中要特别注意不能是当前的数,因为同一个数只能出现一次,因此在传参的时候要把当前的结点信息传进去。
代码时间复杂度从理论上来说应该是O(nlogn)。但由于剪枝效应的存在,所以在实际的运行上还是比较高效的。
public boolean findTarget(TreeNode root, int k) {
return dfs(root, root, k);
}
private boolean dfs(TreeNode root, TreeNode cur, int k) {
if(cur == null) return false;
return search(root, cur, k-cur.val) || dfs(root, cur.left, k) || dfs(root, cur.right, k);
}
private boolean search(TreeNode root, TreeNode cur, int target) {
if(root == null) return false;
if(target == root.val) return root != cur;
else if (target > root.val) return search(root.right, cur, target);
else return search(root.left, cur, target);
}
- 15. 3Sum
问题描述:
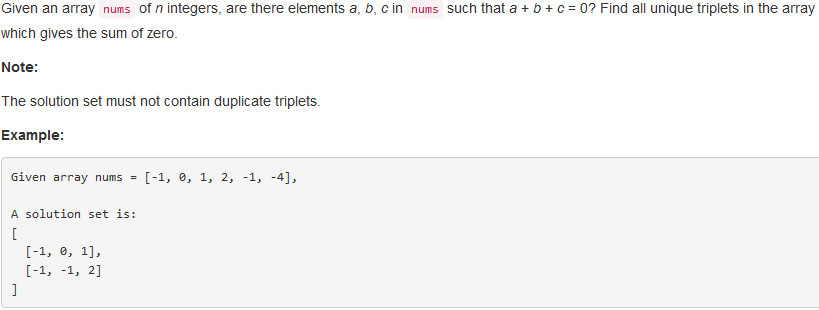
问题求解:
主要的思想就是转化成Two Sum的问题,其中由于结果不能重复,所以我们需要提前对nums进行排序,在排序后,对先后相等的数就可以进行忽略处理了,这样就避免了重复的问题。另外,由于本题中的target = 0,那么在排序后的数组中如果其值大于0,那么也是可以直接排除可能性的,因为其值大于0,其后面的值也必然大于0,因此是不可能存在说三个正数的和为0的。
本题其实也是可以使用dfs + 回溯解决的,但是时间复杂度上会高不少。这里就不多讲解了。
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length - 2; i++) {
if (i == 0 || (nums[i] <= 0 && nums[i] != nums[i - 1])) {
int sum = 0 - nums[i];
int l = i + 1;
int r = nums.length - 1;
while (l < r) {
if (nums[l] + nums[r] == sum) {
res.add(Arrays.asList(nums[i], nums[l], nums[r]));
while (l < r && nums[l] == nums[l + 1]) l++;
while (l < r && nums[r] == nums[r - 1]) r--;
l++;
r--;
}
else if (nums[l] + nums[r] < sum) {
while(l < r && nums[l] == nums[l + 1]) l++;
l++;
}
else {
while(l < r && nums[r - 1] == nums[r]) r--;
r--;
}
}
}
}
return res;
}
-
16. 3Sum Closest
问题描述:

问题求解:
本质上和Three Sum是一样的。
public int threeSumClosest(int[] nums, int target) {
int min = Integer.MAX_VALUE;
int res = Integer.MAX_VALUE;
Arrays.sort(nums);
for (int i = 0; i < nums.length - 2; i++) {
if (i == 0 || nums[i] != nums[i - 1]) {
int sum = target - nums[i];
int l = i + 1;
int r = nums.length - 1;
while (l < r) {
if (nums[l] + nums[r] == sum) {
return target;
}
else if (nums[l] + nums[r] < sum) {
if (min > sum - (nums[l] + nums[r])) {
min = sum - (nums[l] + nums[r]);
res = nums[i] + nums[l] + nums[r];
};
while (l < r && nums[l + 1] == nums[l]) l++;
l++;
}
else {
if (min > nums[l] + nums[r] - sum) {
min = nums[l] + nums[r] - sum;
res = nums[i] + nums[l] + nums[r];
};
while (l < r && nums[r - 1] == nums[r]) r--;
r--;
}
}
}
}
return res;
}
-
18. 4Sum
问题描述:

问题求解:
转化成Three Sum就好了。
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length - 3; i++) {
if (i == 0 || nums[i] != nums[i - 1]) {
for (int j = i + 1; j < nums.length - 2; j++) {
if (j == i + 1 || nums[j] != nums[j - 1]) {
int sum = target - nums[i] - nums[j];
int l = j + 1;
int r = nums.length - 1;
while (l < r) {
if (nums[l] + nums[r] == sum) {
res.add(Arrays.asList(nums[i], nums[j], nums[l], nums[r]));
while (l < r && nums[l + 1] == nums[l]) l++;
while (l < r && nums[r - 1] == nums[r]) r--;
l++;
r--;
}
else if (nums[l] + nums[r] < sum) {
while (l < r && nums[l + 1] == nums[l]) l++;
l++;
}
else {
while (l < r && nums[r - 1] == nums[r]) r--;
r--;
}
}
}
}
}
}
return res;
}
- 416. Partition Equal Subset Sum
问题描述:
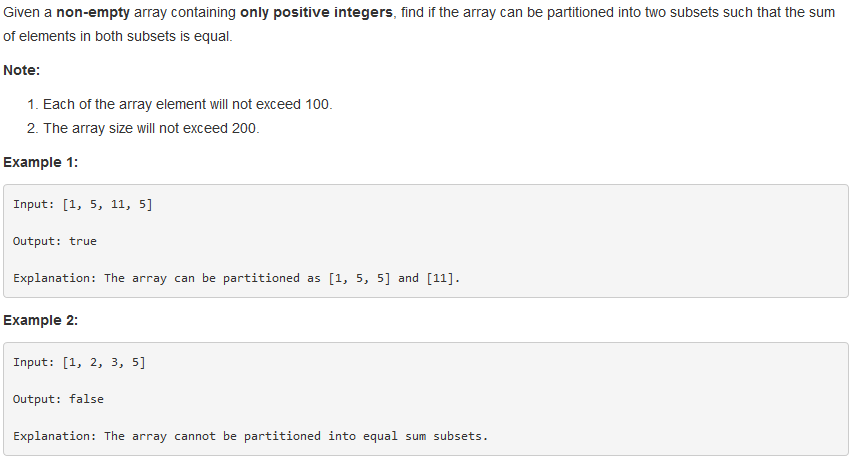
问题求解:
其实就是一个背包问题,这里就是在看能不能挑其中n个物品,使其和为sum/2。当然,首先sum应该是偶数,如果sum奇数,那么就可以直接返回结果。
public boolean canPartition(int[] nums) {
int sum = 0;
for (int i : nums) sum += i;
if (sum % 2 != 0) return false;
sum /= 2;
boolean dp[] = new boolean[sum + 1];
dp[0] = true;
for (int num : nums) {
for (int i = sum; i >= num; i--) {
dp[i] = dp[i] || dp[i - num];
}
}
return dp[sum];
}
-
494. Target Sum
问题描述:
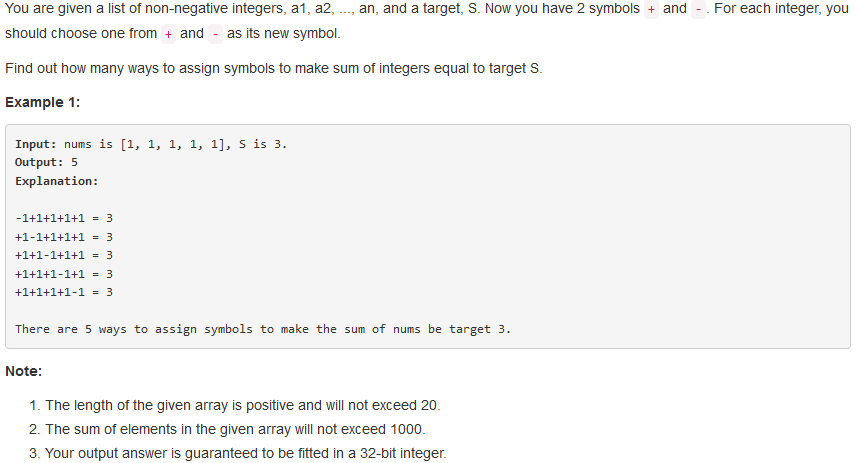
问题求解:
方法一、第一个方法就是暴力搜索,回溯枚举。时间复杂度为指数级。
public int findTargetSumWays(int[] nums, int S) {
if (nums.length == 0) return 0;
return helper(nums, 0, S);
}
private int helper(int[] nums, int idx, int S) {
if (idx == nums.length) {
if (S == 0) return 1;
else return 0;
}
int res = 0;
res += helper(nums, idx + 1, S + nums[idx]);
res += helper(nums, idx + 1, S - nums[idx]);
return res;
}
方法二、这个方法很有技巧性,实际上是把原问题转化成了求部分和的问题。不妨设+部分和为P,-部分和为Q,则P - Q = S,又P + Q = sum,所以得到2P = S + sum。也就是说求解nums中部分和为(S + sum)/ 2的总个数。由于原问题中指出了数字非负性,所以这种方法是可行的。算法的时间复杂度为伪多项式时间复杂度。
必须要多sum 和 S 的大小进行判断,因为S的大小可能远超sum,这个时候如果不加判断会MLE。
public int findTargetSumWays(int[] nums, int S) {
int sum = 0;
for (int i : nums) sum += i;
if (sum < S || sum + S < 0 || (sum + S) % 2 != 0) return 0;
return helper(nums, (sum + S) / 2);
}
private int helper(int[] nums, int S) {
int[] dp = new int[S + 1];
dp[0] = 1;
for (int num : nums) {
for (int i = S; i >= num; i--) {
dp[i] += dp[i - num];
}
}
return dp[S];
}