2018-03-07 19:01:21
void X_Sort ( ElementType A[], int N )
1)N是正整数
2)只讨论基于比较的排序(> = < 有定义)
3)只讨论内部排序:所有内容都在内存中
4)稳定性:任意两个相等的数据,排序前后的相对位置不发生改变
5)没有一种排序是任何情况下都表现最好的
一、简单排序
- 冒泡排序
冒泡排序:稳定,且对链表排序适用。

- 插入排序

对简单排序的分析:
对于插入排序来说,其算法时间复杂度本质上是O(N + I),其中N是数组的规模,I是逆序对的个数。一个随机数组中的逆序对的的期望个数是O(n(n - 1) / 4)。所以如果单纯的使用交换相邻数来进行排序,那么其算法的时间复杂度的下界就是O(n^2)。因此,我们不能每次仅仅消去一个逆序对,而是要寻找方法,一次消去多个逆序对来提高效率。


二、希尔排序
希尔排序的提出正是为了解决在插入排序中仅仅交换相邻元素带来的逆序对无法一次消去多个的问题,在希尔排序中,间隔不再是1,而是一个增量序列,通过改变间隔,期望能够达到每次消去不止1个逆序对的目的。


由于原始的希尔排序中增量序列之间的不互质性,导致可能在最后的1间隔前做了很多的无用功,大大降低了算法的效率。于是有学者提出了改进的增量序列来提高希尔排序的算法复杂度。

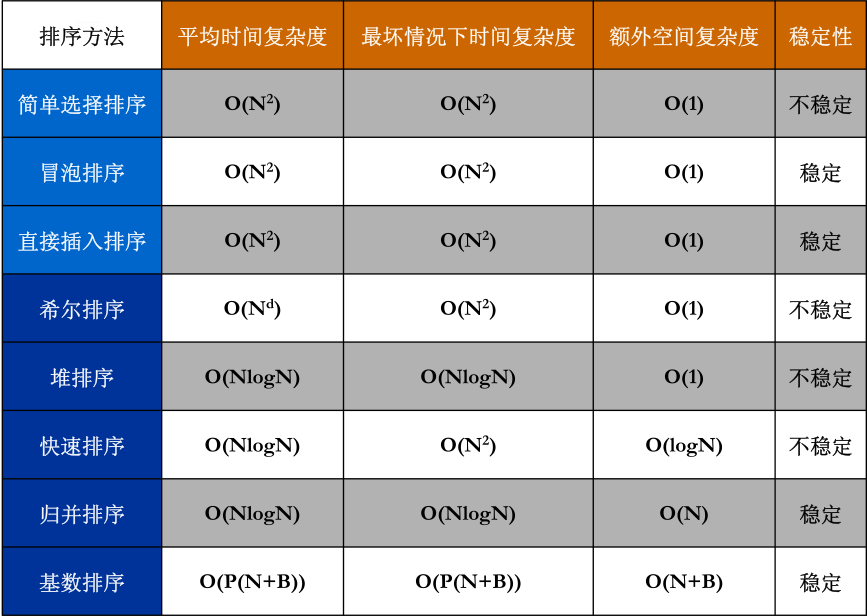
三、堆排序
在讲解堆排序前,先提一下选择排序。所谓选择排序就是每次选择当前待排序序列中的最小元素,将之与已排序的末尾元素交换。可以看到,最后的交换过程中,并不是相邻元素的交换,有可能一次消去多个逆序对,因此,选择排序不是稳定排序。

如果我们使用堆来寻找最小元,这就有了堆排序,堆排序也是不稳定的排序。
方法一、非常单纯的做法是建立一个最小堆,然后每次删除根结点,同时用一个数组加之保存。但是这种方案的缺点是很明显的,首先需要额外开辟空间,其次最后还需要将元素重新导回原数组,非常浪费时间。

方法二、在原数组上构造一个最大堆,每次将堆顶元素与末尾置换,规模减一,然后向下调整,直到最后一个元素即可。这样的方法就是完全的原址运算,避免了另外开辟空间和复制的开销。
四、归并排序
归并排序的时间复杂度是严格的O(nlogn),且是稳定的排序。由于需要开辟一个额外的O(n)的空间作为中转,所以在实际的使用过程中,内排序基本不使用归并排序。归并排序在外排序的时候会有很大的作用。
归并排序的核心算法是归并操作: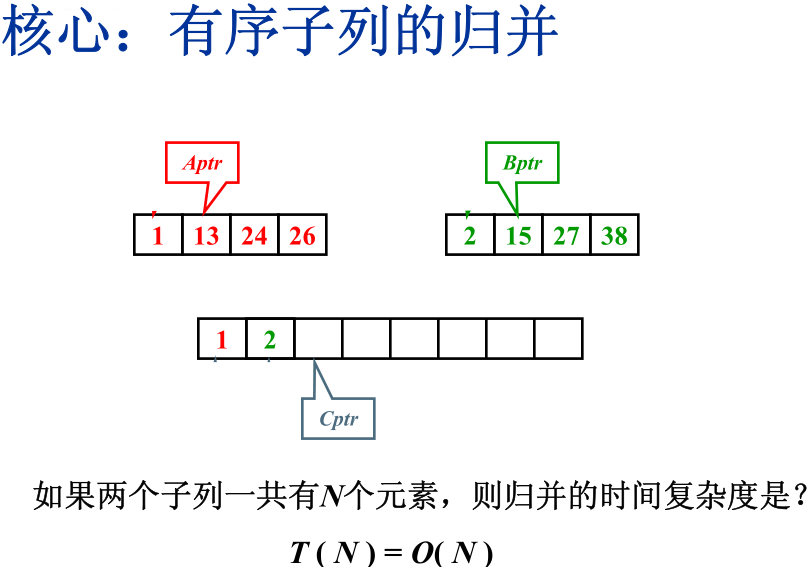

- 递归实现
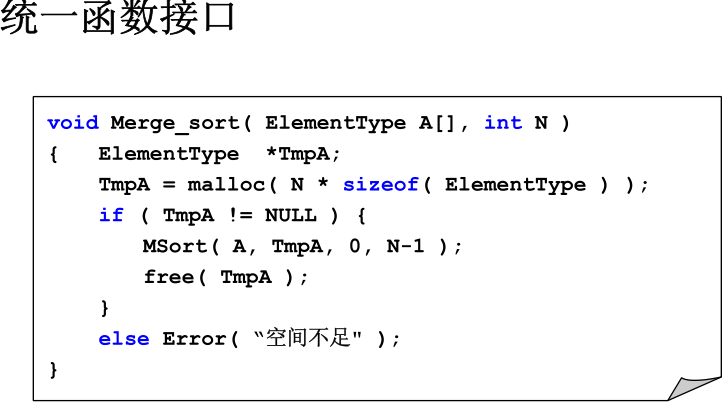

- 非递归实现
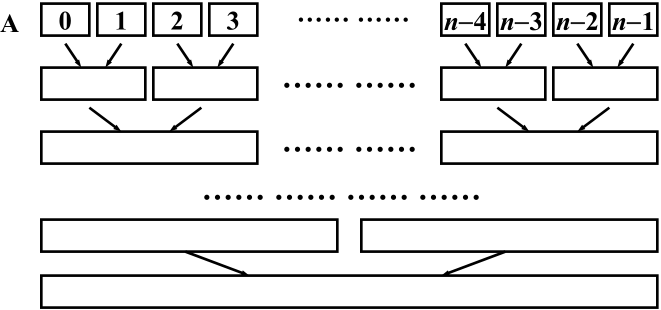


五、快速排序
快速排序和归并排序类似的是都采用了递归的思想来处理问题。
快速排序的最优情况是每次主元都均分,快排是不稳定排序。
需要注意的是快速排序比较适用于大规模的排序,如果待排数组个数小于100,其效率甚至不如冒泡排序。
int partition(vector<int>&,int,int);
void qsort(vector<int>& vec,int p,int r)
{
if(p<r)
{
int q=partition(vec,p,r);
qsort(vec,p,q-1);
qsort(vec,q+1,r);
}
}
int partition(vector<int>& vec,int p,int r)
{
int i=p-1;
int temp=vec[r];
for(int j=p;j<=r-1;++j)
{
if(vec[j]<temp) swap(vec[++i],vec[j]);
}
swap(vec[++i],vec[r]);
return i;
}
六、表排序
表排序适用于待排元素是一个结构体,或者说一个很庞大的数据,如果使用简单排序,那么swap的消耗就无法忽略。
表排序在排序过程中不移动元素本身,而只移动元素的指针,这种不移动元素的方法称为间接排序。
表排序从本质上来说就是对table数组中的指针值对应的真实的值进行排序。
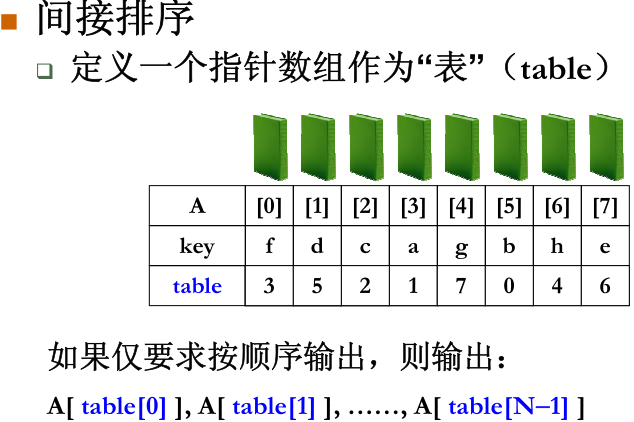
如果需要在物理上也实现排序,那么可以在间接排序的基础上进行调整。考虑到N个整数的序列是由若干不相交的环构成的,所以我们可以对每一个环进行微调,对每个调整正确的将之在table中的数值改为A的序号,表明现在其已经在合适的位置。

复杂度分析:

七、基数排序
通过决策数的分析我们可以得到基于比较的排序算法其算法的最坏情况下的下界是O(nlogn)。也就是说在最坏条件下,选择性能最好的排序算法也就只能得到O(nlogn)的算法。
难道O(nlogn)就是排序算法难以突破的五指山么?答案是否定的,如果是采用基数排序,就可以完成突破。基数排序是稳定排序。
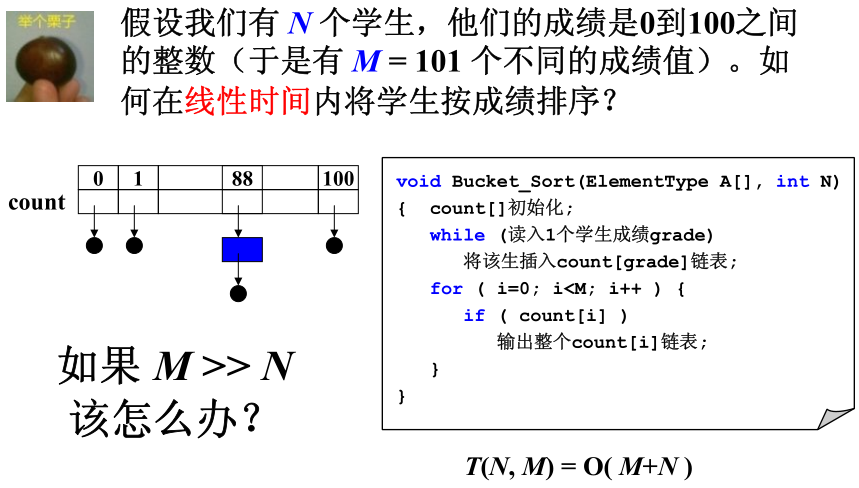
- 桶排序
桶排序是基数排序的简化版,或者说基数排序是桶排序的升级版。
桶排序适用于待排数据为一特定范围的数组。我们可以为这些数据建造不同的桶,然后遍历一遍数组,分别将数字放到自己的桶里即可完成排序。
- 基数排序
在某种情况下,M>>N,就导致了如果单纯的按照桶排序,那么就会造成极大的浪费和开销。这时候就可以使用基数排序来解决这个问题。
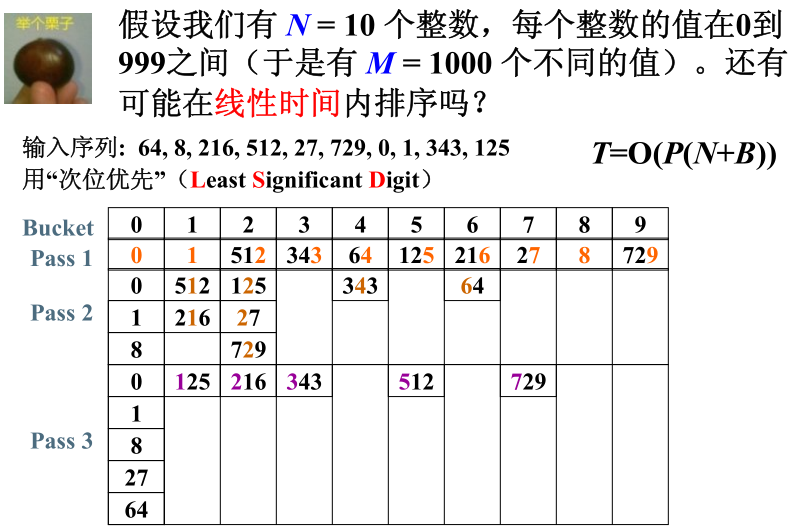
基数排序在多关键字的排序上也有应用。显然在下面的问题中使用次位优先是比较优越的方法,如果使用的高位优先,那么则需要在每个桶中再次使用普通的排序方法,这样无疑会加大基数排序的时间复杂度。
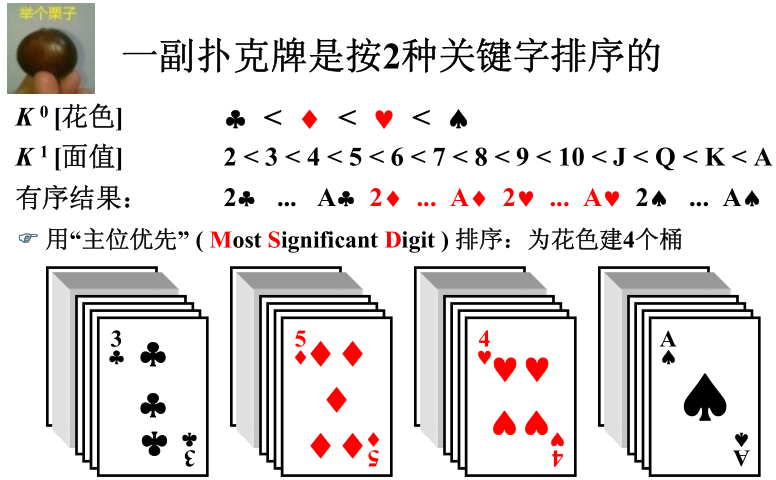
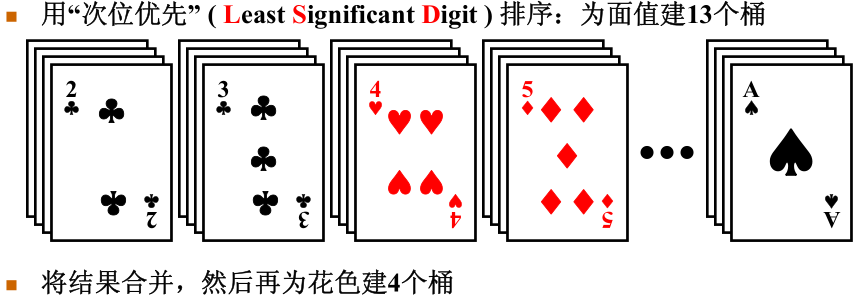
八、排序算法总结