2018-03-05 16:19:46
图是计算机科学中的一个非常重要的概念,图是一种多对多的关系。从某种角度上来说树和链表都是图的一种特例。

一、图的抽象数据类型

二、表示图的方法
图是由结点和边构成的,只要能通过某种方式将结点和边的信息表示出来就可以了。以下是两种最常见的图的表示方法,值得一提的是,并不是只有这两种方法来表示图。
- 邻接矩阵
邻接矩阵G[N][N]——N 个顶点从0 到N-1 编号。
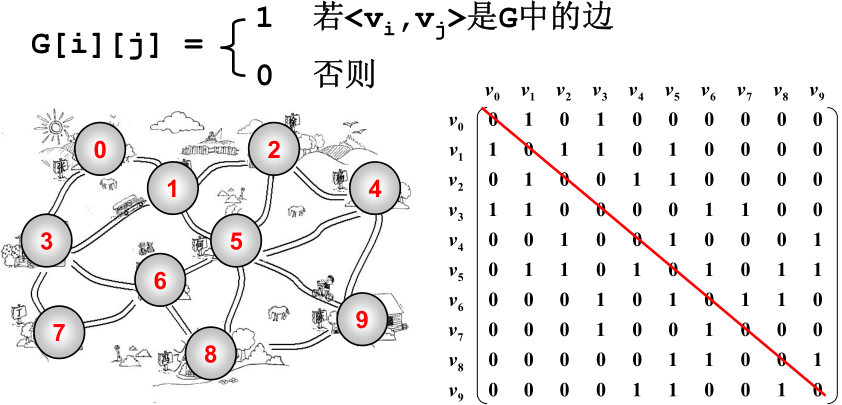
对于无向图,邻接矩阵是对称的,所以可以只保存下三角来减少一半的空间开销。
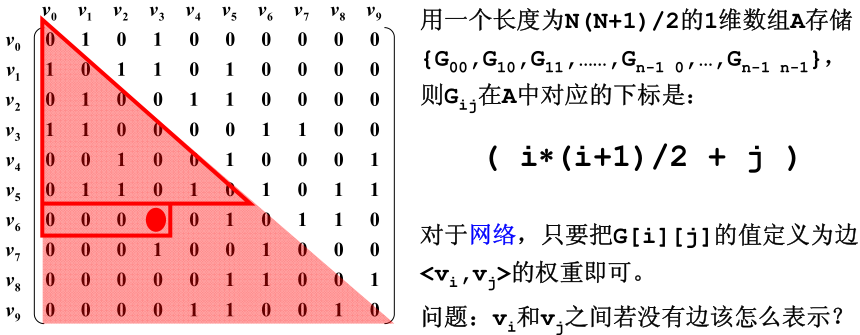
邻接矩阵的优点:
- 直观、简单、好理解
- 方便检查任意一对顶点间是否存在边
- 方便找任一顶点的所有“邻接点”(有边直接相连的顶点)
- 方便计算任一顶点的“度”(从该点发出的边数为“出度”,指向该点的边数为“入度”)
邻接矩阵的缺点:
- 浪费空间:对于稀疏的图将存放大量无用的数据;
- 浪费时间:比如查找一个结点的邻接点,需要将所有的结点遍历一遍;
- 邻接表
邻接表:G[N]为指针数组,对应矩阵每行一个链表,只存非0元素,也就是直接相邻的结点。一定要足够的稀疏才合算。
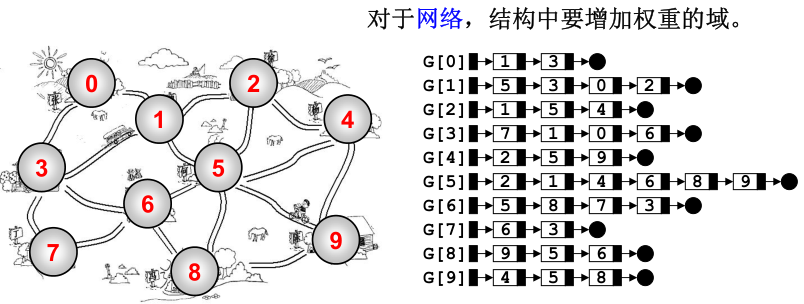
邻接表的特点:
- 方便找任一顶点的所有“邻接点”
- 节约稀疏图的空间(需要N个头指针 + 2E个结点(每个结点至少2 个域))
- 方便计算任一顶点的“度”:仅对于无向图,如果是有向图,那么只能很快的计算出度,入度的计算还是有难度的
- 相对于邻接矩阵,邻接表并不适合很快的查找两个结点之间是否存在边
三、图的遍历
类似于二叉树的遍历,图的遍历也有两种策略,一是深度优先,二是广度优先。
- DFS
所谓遍历,就是将图中所有的结点访问一次,且仅一次。深度优先搜索就是每次到达一个结点,首先申明我访问过他了,避免二次访问,然后在其邻接的结点中挑选是否有还没有被访问的,访问之,重复进行该项操作,即可。
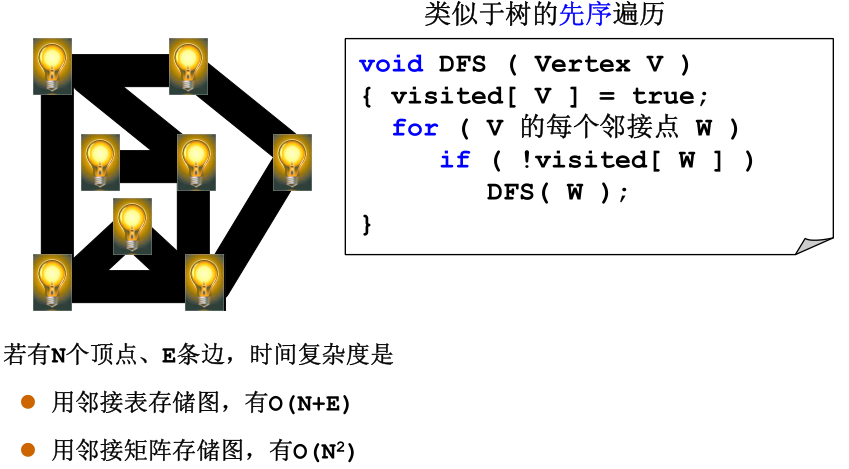
- BFS
BFS类似于二叉树中的层序遍历,使用队列来保存将要访问的结点信息。
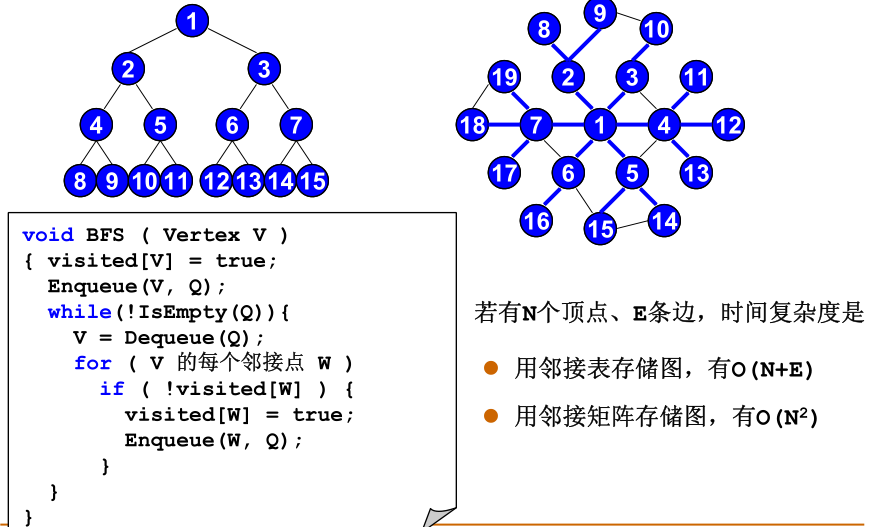
在遍历的过程中,还有一个特别重要的概念--连通性。
连通分量 :无向图的极大连通子图
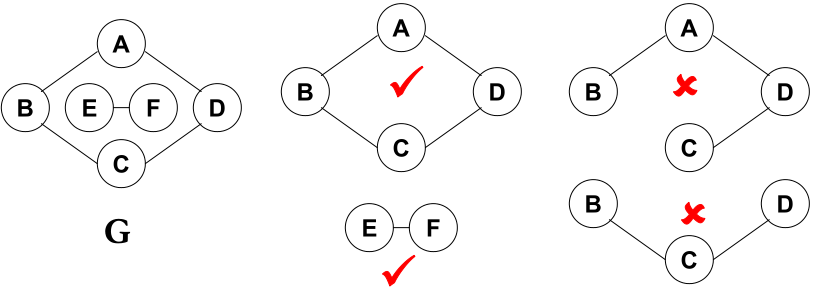
强连通 :有向图中顶点V和W之间存在双向路径,则称V和W是强连通的。
强连通图 :有向图中任意两顶点均强连通
强连通分量 :有向图的极大强连通子图
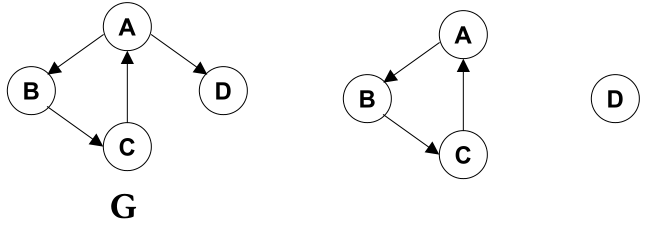
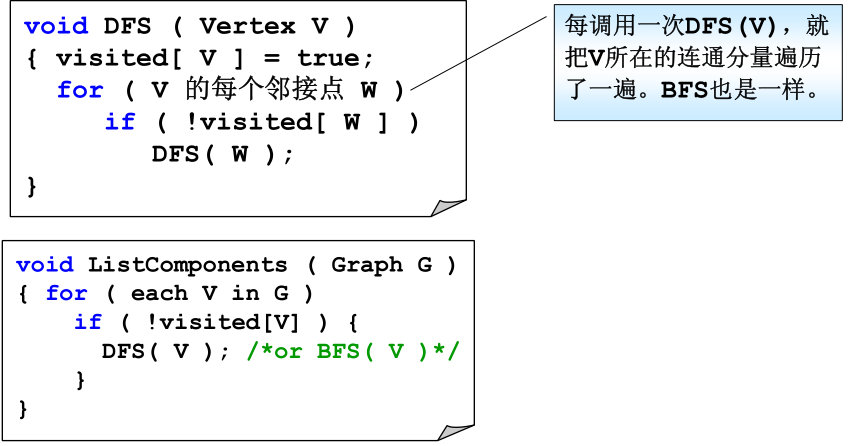
对于不连通的图可以对每个连通分量做一次DFS(或者BFS)。
四、应用实例
问题一:解救007
问题描述:詹姆斯邦德被困在孤岛上,孤岛周围环绕的鳄鱼,他的跳跃半径已知,在其跳跃半径内,他可以跳上鳄鱼的头。试问其是否可以上岸。

问题求解:该问题中的结点有孤岛,鳄鱼和岸。请注意,这里岸也是一个结点,所谓的结点其实是一个非常抽象的概念。问题要求的其实就是在这个图中是否可以在遍历过程中遍历到岸这个结点,如果可以那么就返回TRUE。
那是否需要构造一个邻接矩阵,或者邻接表呢?答案是否定的,就像之前提到的,不是说图都要用这两种表示方法来描述,这一题中,可以直接对两个鳄鱼之间的距离进行判断,就可以得到是否存在边的信息。


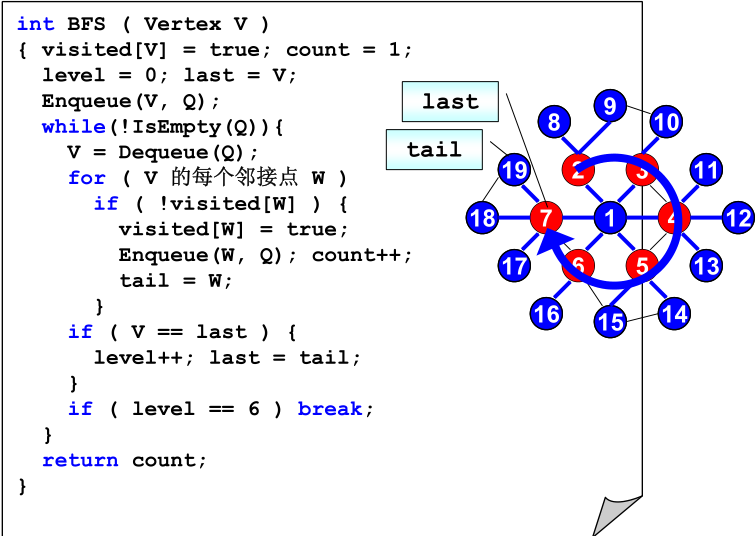
问题二:六度空间
问题描述:
六度空间理论,你和任何一个陌生人之间所间隔的人不会超过六个。
现给定社交网络图,请对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
问题求解:
按层序遍历,主要的难点就是如何保证只遍历到6层就结束。当然,有种简单的方式就是给每个结点增加一条层数信息,但是这样毫无疑问是非常消耗空间的,这里给出了一种O(1)的解决层数记录的方法,非常巧妙。