散列表

2018-02-24 23:54:41

散列表（Hash table，也叫哈希表），是根据键（Key）而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

问题：如何快速搜索到需要的关键词？如果关键词不方便比较怎么办？

求解：查找常用的方法有二分查找(O(lgn))，二叉搜索树查找(O(h))，平衡二叉搜索树查找(O(lgN))等。但是对于关键词不方便比较的问题，使用任意一种方法都不是很方便。这时可以使用散列表。

查找的策略：查找的本质是根据所给的关键词，找到相应的位置。

1）有序安排对象：全序、半序 -- 二分查找

2）根据关键词计算出位置 -- 散列

散列查找法的两项基本工作：

1. 计算位置：构造散列函数计算关键词的存储位置。
   
2. 解决冲突：解决多个关键词计算得到的位置相同的问题。

如果散列函数构造合理，冲突解决方案合适，那么操作的时间复杂度可以达到O(1)。

一、散列表的抽象数据类型

散列的基本思想是：

（1）以关键字key为自变量，通过噢一个确定的函数h（散列函数），计算出对应的函数值h（key），作为数据的存储位置；

（2）可能不同的关键字会映射到同一个存储位置上，这别称为冲突，所以需要某种冲突解决策略。

二、散列函数

一个‘好’的散列函数一般要考虑下列的两个因素：

1）计算简单，以便提高转换效率；

2）关键字对应的地址空间分布均匀，以减少冲突的发生；

•  数字关键字

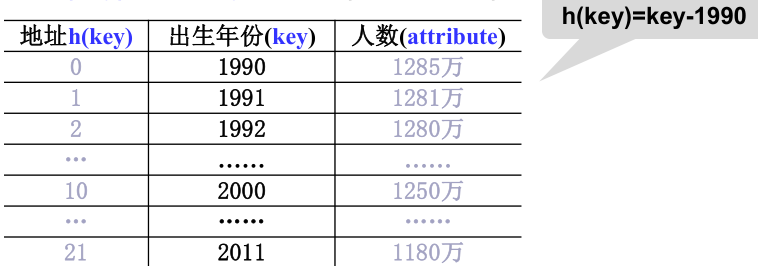
1）直接定址法

取关键词的某个线性函数值为散列地址，即：

h(key) = a * key + b (a 、b 为常数)

2）除留余数法

散列函数为：

h(key) = key mod p

 

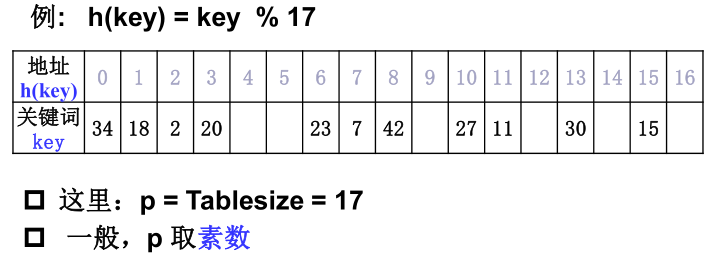
关于除数为什么选择素数的理解：

假设N = kn, M = km， N和M存在最大公因数k，此时可以将N % M = r转化为公式N = Mq + r，即kn = kmq + r。其中q是商，r是余数。“表面上”r的取值范围是{0, 1, 2, …, M-1}（忽视了只有N与M最大公因数为1时，才能取整个余数集合R的定理），一片和谐。但是可以对公式进行稍微的变换，n = mq + (r/k)，由于n和mq都是整数，则(r/k)也是整数。此时我们看一看到(r/k)的取值范围是{0, 1, 2, …, m} = {0, 1, 2, …, M/k}。恢复到原式，也是就r的“实际”取值范围是{0, k, 2*k, 3*k, …, m*k}，缩小了k倍。

一切都明了了，我们最后的目标就是保证N与M最大公因数为1。最简单的方式就是直接取M为质数！

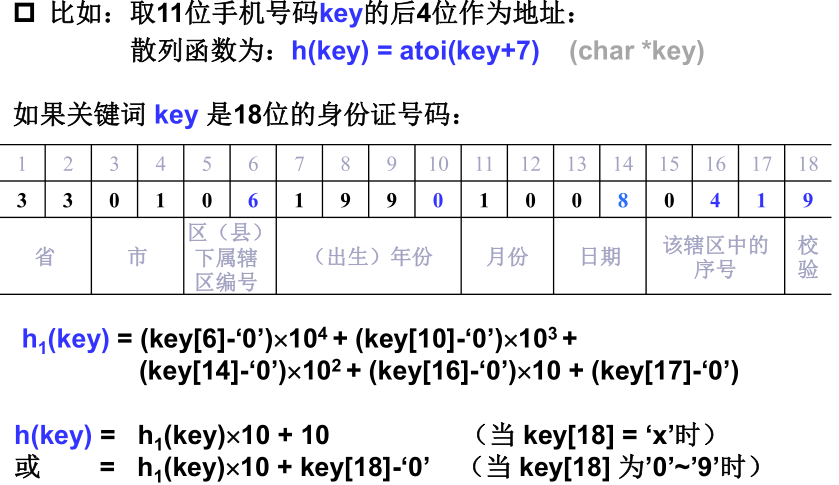
3）数字分析法

分析数字关键字在各位上的变化情况，取比较随机的位作为散列地址。

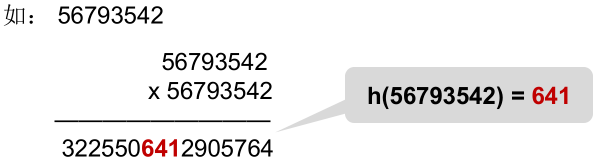
4）折叠法

5）平方取中法

• 字符串关键字

1）简单的ASCII码加和取mod法

冲突严重，比如a3 、b2 、c1 ；eat 、 tea ；

h(key) = (Σkey[i]) mod TableSize

2）好的散列函数——移位法

涉及关键词所有n 个字符，并且分布得很好：

三、冲突处理

处理冲突的方法：

1. 换个位置: 开放地址法
2. 同一位置的冲突对象组织在一起: 链地址法

•  开放定址法（Open Addressing）

一旦产生了冲突某（该地址已有其它元素），就按某种规则去寻找另一空地址。

若发生了第 i  次冲突，试探的下一个地址将增加d i ，基本公式是：

h i (key) = (h(key)+d i ) mod TableSize ( 1≤ i < TableSize )

 

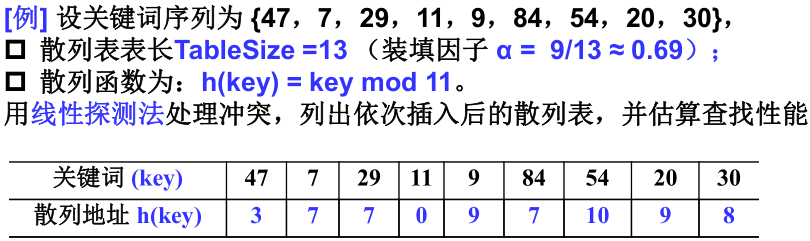
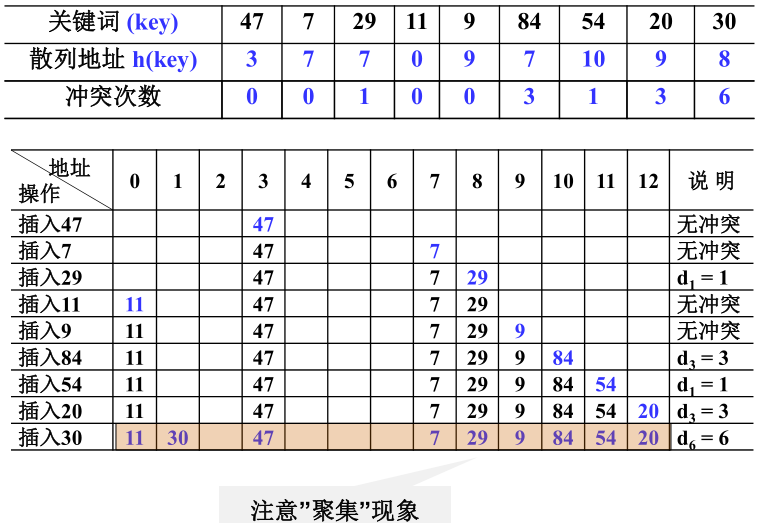
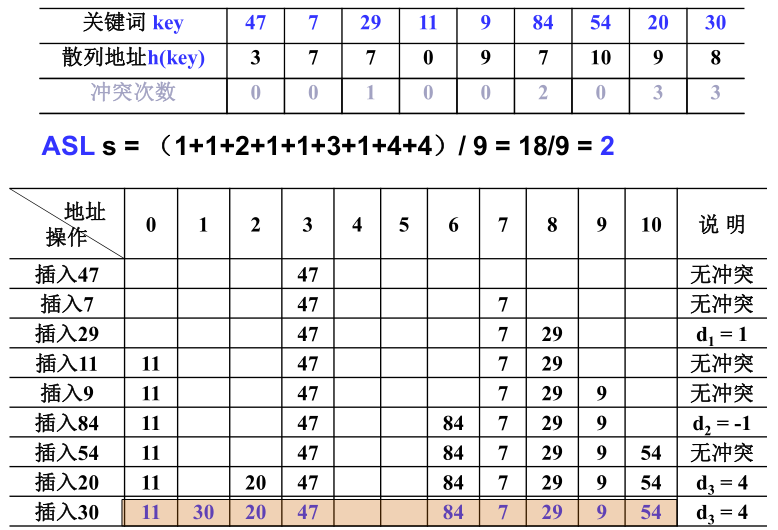
1）线性探测法（Linear Probing）

线性探测法 ： 以列增量序列 1 ，2，……，（TableSize -1）。循环试探下一个存储地址。

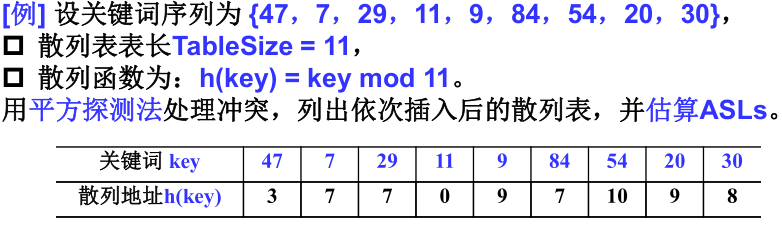
2）平方探测法（Quadratic Probing）--- 二次探测

线性探测的方法就是每次遇到冲突就依次往后找空位，显然，这种方法很容易就会造成聚集的现象，也就是在一片区域大面积的冲突，为了解决这个问题又提出了平方探测法。

所谓平方探测法，其实也很好理解，就是把刚刚的+i，变成了+-i^2。具体来说，如下：

这里的q <= tableSize/2的原因是，当从1递增到q进行检索的时候，实际尝试的位置是2*q，如果继续增大q毫无疑问会发生重复，另外，有定理已经证明了，从1到q是互异的，这也就从理论上说明了，这种平方探测可以完全遍历整个空间。

定理：如果散列表长度TableSize是某个4k+3（k 是正整数）形式的素数时，平方探测法就可以探查到整个散列表空间。

在开放地址散列表中，删除操作要很小心。通常只能“ 懒惰删除 ”，即需要增加一个“ 删除标记(  Deleted ) ” ，而并不是真正删除它。以便查找时不会“ 断链 ”。其空间可以在下次插入时重用。

3）双散列探测法（Double Hashing）

上面提到的方法都是直接对偏移量进行数学运算，在双散列法中提出偏移量本身也是一个散列函数。

4）再散列（Rehashing）

• 链地址法

分离链接法：将相应位置上冲突的所有关键词存储 在同一个单链表中。

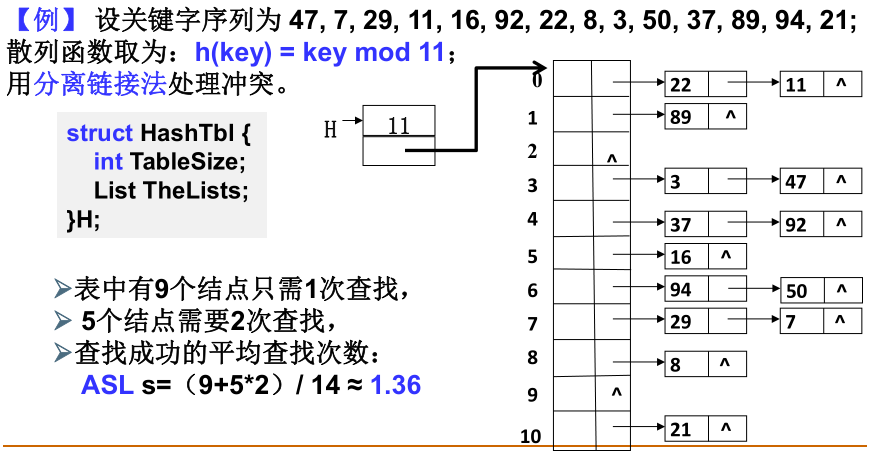
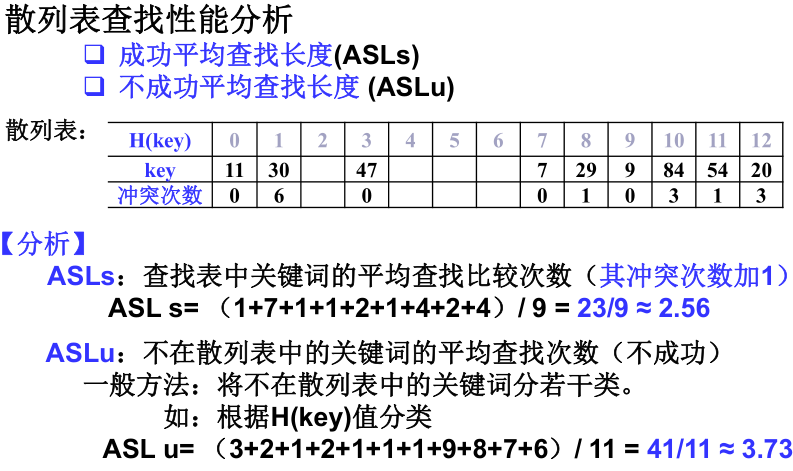
四、散列表的性能分析

平均查找长度（ASL）用来度量散列表查找效率：成功、不成功。

影响散列的性能的三个主要因素是：

1. 散列函数是否均匀；
2. 处理冲突的方法；
3. 散列表的装填因子α；

1）线性探测法的查找性能

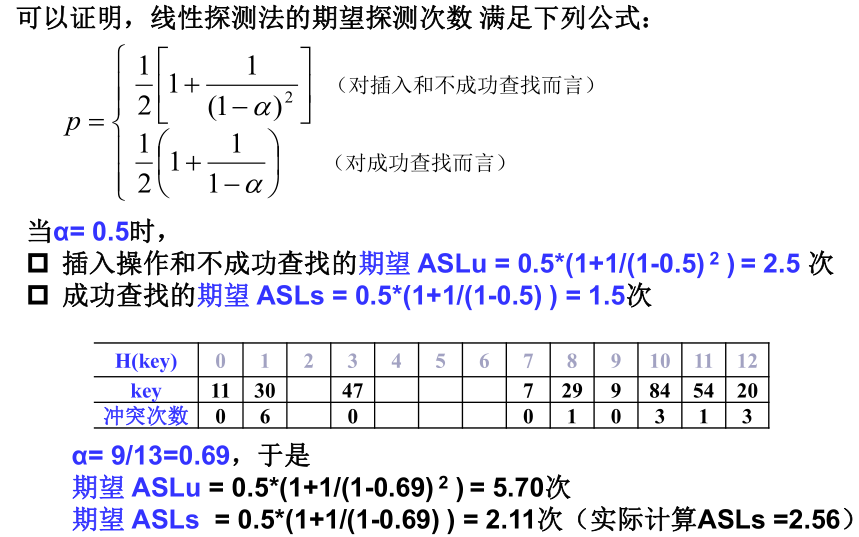
2）平方探测法和双散列探测法的查找性能

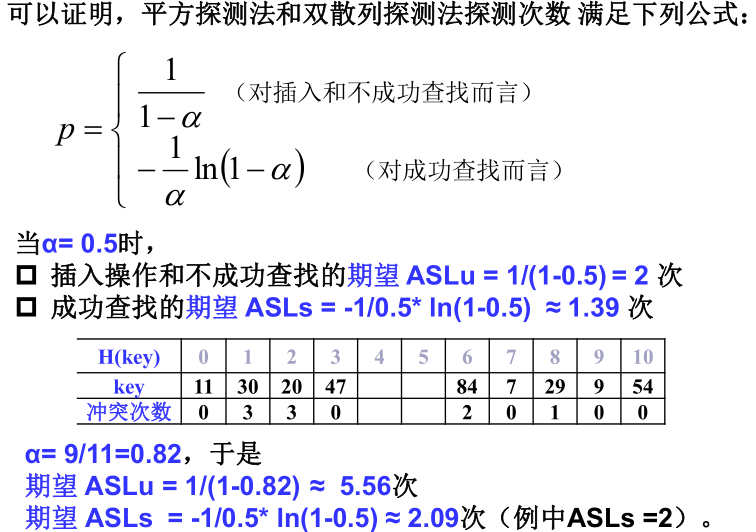
3）分离链接法的查找性能

4）期望探测次数与装填因子α的关系

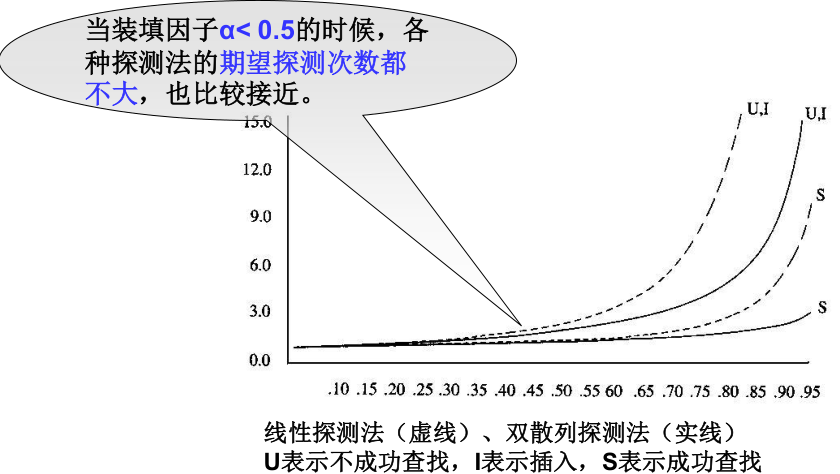
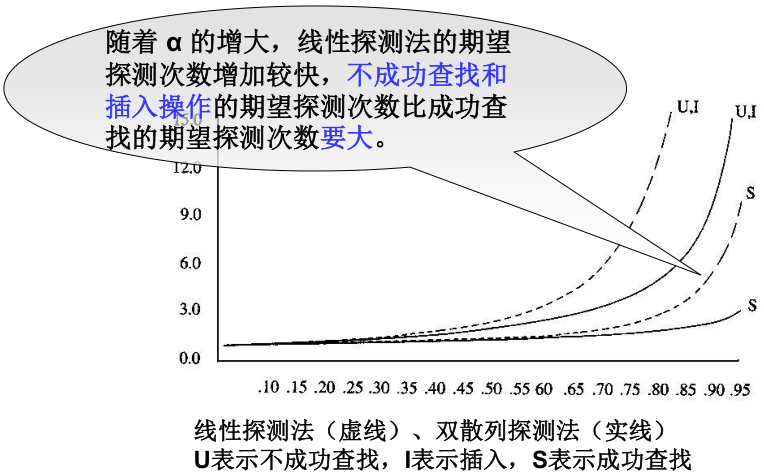
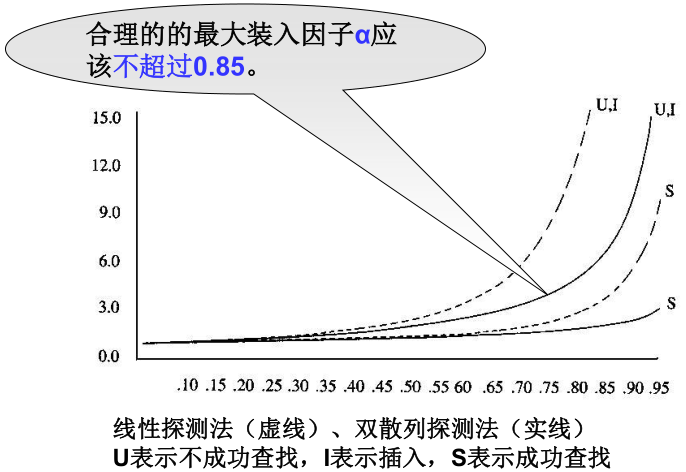
五、总结